Công thức Toán học
Công thức tính diện tích toàn phần hình trụ đơn giản, dễ ghi nhớ
Công thức tính diện tích toàn phần hình trụ là công thức khá cơ bản trong chương trình giáo dục phổ thông mà ai cũng cần phải nắm vững. Bên cạnh đó, hình trụ được ứng dụng rất nhiều trong các ngành, các lĩnh vực khác nhau và cả trong đời sống hằng ngày.
Công thức tính thể tích khối tròn xoay, điều kiện áp dụng và tầm quan trọng
Thể tích khối tròn xoay là một trong những dạng bài toán hình học không gian cực kỳ thú vị. Khi áp dụng chính xác công thức, bạn có thể dễ dàng tính được thể tích của một vật thể dạng khối trụ tròn xung quanh trục Ox và Oy. Nếu bạn chưa biết tính thể tích khối tròn xoay, tham khảo bài viết dưới đây để thành thạo áp dụng vào thực tế.
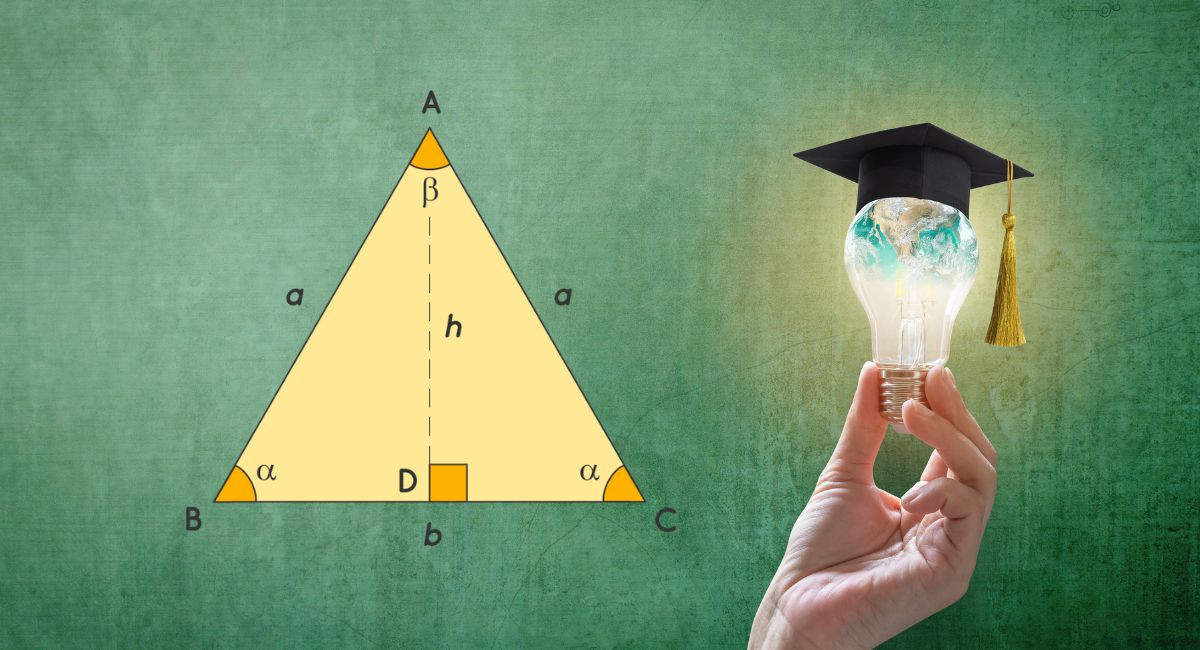
Tính diện tích tam giác cân: Công thức đầy đủ và ví dụ minh họa
Các bài toán tính diện tích tam giác cân hóc búa không thể làm khó bạn nếu nắm vững những công thức độc quyền cùng ví dụ minh họa chi tiết dưới đây. Được hệ thống khoa học và trình bày dễ hiểu, bạn sẽ dễ dàng chinh phục mọi dạng bài tập về diện tích tam giác cân, từ cơ bản đến nâng cao.
Diện tích tam giác vuông: Từ A-Z về công thức và cách làm
Diện tích tam giác vuông là một chủ đề quan trọng trong chương trình toán học cơ bản, đóng vai trò nền tảng cho nhiều ứng dụng thực tế. Để giải quyết các bài toán liên quan đến diện tích tam giác vuông một cách hiệu quả, học sinh cần chú ý đến hai yếu tố then chốt: nắm vững công thức và phân chia đúng dạng bài tập.
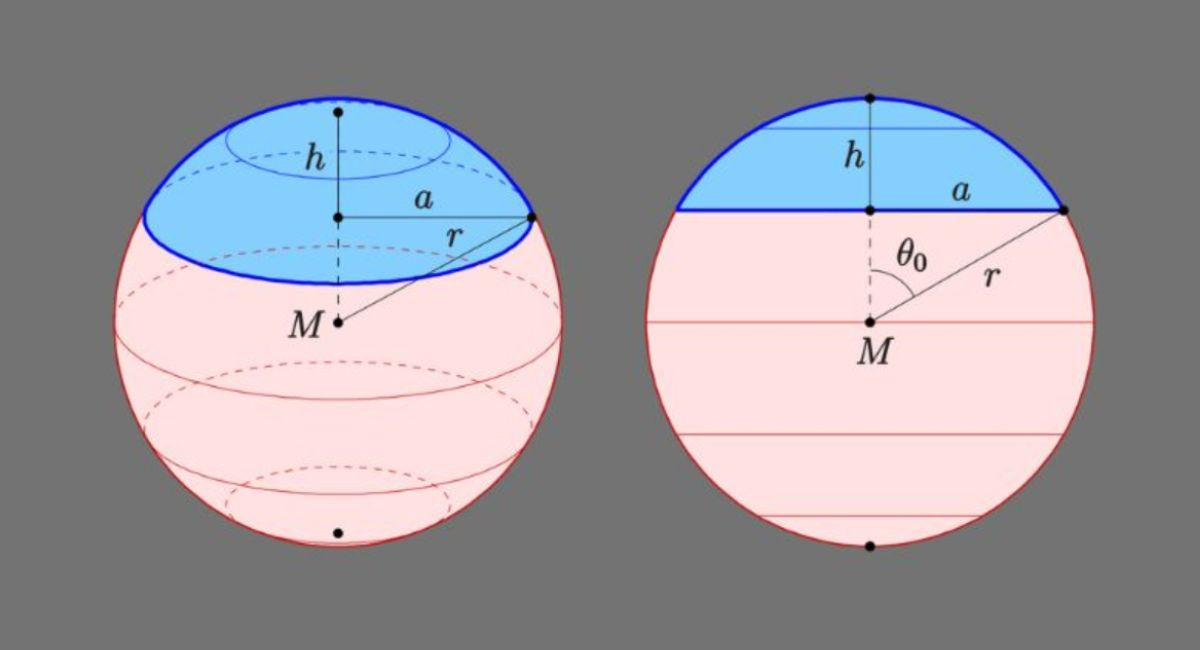
Áp dụng công thức tính thể tích hình cầu chuẩn sách giáo khoa
Công thức tính thể tích hình cầu là V = 4.π.r3/3. Trong đó, r là bán kính của hình cầu, π là hằng số toàn học, có giá trị xấp xỉ bằng 3,14 và V là thể tích hình cầu. Thể tích hình cầu không chỉ là một khái niệm quan trọng trong toán học mà còn được áp dụng ở nhiều lĩnh vực trên thực tế.
Công thức tính thể tích hình lập phương chính xác, nhanh chóng
Biết cách tính thể tích hình lập phương là một kỹ năng quan trọng mà học sinh cần nắm vững để giải các bài toán liên quan đến hình học không gian. Tuy nhiên, để giải các bài toán về thể tích hình lập phương một cách hiệu quả, học sinh cần rèn luyện sự linh hoạt trong tư duy và phương pháp giải.
Thể tích hình hộp chữ nhật và 5 dạng toán nhất định phải học
Dạng toán tính thể tích hình hộp chữ nhật dựa trên mối liên hệ giữa thể tích và kích thước của hình hộp. Cụ thể, thể tích của hình hộp chữ nhật được tính bằng tích của chiều dài, chiều rộng và chiều cao của nó.
Diện tích mặt hình cầu: Công thức và các dạng bài có lời giải
Dạng bài tập tính diện tích mặt hình cầu là một phần quan trọng trong chương trình học Toán THCS và THPT. Thông qua việc thành thạo cách tính diện tích của mặt cầu, bạn có thể ứng dụng vào thực tế cho quá trình thiết kế, thi công của các công trình và thiết bị liên quan.
Diện tích xung quanh hình trụ: Tổng hợp các dạng bài hay nhất
Diện tích xung quanh hình trụ là diện tích của mặt bao quanh hình trụ, được tính bằng tích của chu vi đáy và chiều cao của hình trụ. Thành thạo cách tính toán diện tích hình trụ, bạn có thể áp dụng vào nhiều bài toán thực tế như tính toán diện tích vật liệu cần thiết để làm vỏ hộp, diện tích tản nhiệt của động cơ.
Hướng dẫn chi tiết các cách tính chu vi hình tam giác có ví dụ minh họa
Tính chu vi của hình tam giác là một kỹ năng toán học thiết yếu, giúp giải quyết các bài toán liên quan đến diện tích, góc, đường cao,... Bài viết này sẽ trình bày một cách khoa học và chi tiết các phương pháp tính chu vi hình tam giác, bao gồm tam giác đều, tam giác cân, tam giác vuông và tam giác bất kỳ.
Diện tích toàn phần hình chóp nón: Đọc để bài tập trở nên dễ dàng
Các bài toán diện tích toàn phần hình chóp nón cơ bản thường chỉ yêu cầu áp dụng công thức trực tiếp, trong khi các bài toán nâng cao có thể đòi hỏi học sinh phải vận dụng nhiều kỹ năng toán học hơn như: chứng minh, giải phương trình, lập phương trình,...
Tính diện tích xung quanh hình lập phương siêu dễ cùng những ứng dụng thực tế
Việc tính diện tích xung quanh hình lập phương là một kỹ năng cơ bản mà học sinh cần nắm vững để giải các bài toán về hình học không gian. Tuy nhiên, nhiều học sinh còn gặp khó khăn trong việc giải các bài toán dạng này do chưa luyện tập thường xuyên.
Diện tích hình thang: Tổng hợp mọi dạng bài và công thức dễ nhớ
Tính diện tích hình thang là một trong những bài toán cơ bản trong toán học. Trên thực tế, việc giải quyết các bài toán này không chỉ là việc áp dụng công thức mà còn yêu cầu sự tỉ mỉ, cẩn thận trong cách xác định thông số và tính toán.
Cách tính chu vi hình vuông đơn giản cùng ứng dụng trong thực tiễn
Tính chu vi hình vuông là một chủ đề toán học cơ bản từ cấp tiểu học. Bài viết này sẽ trình bày một cách hệ thống và khoa học về các phương pháp tính chu vi hình vuông. Với nội dung được trình bày rõ ràng, súc tích cùng các ví dụ minh họa cụ thể, người đọc sẽ dễ nắm bắt kiến thức hơn.
Diện tích hình tròn: Tổng hợp mọi dạng bài từ dễ tới khó
Việc nắm vững kiến thức về diện tích hình tròn là nền tảng giúp học sinh giải quyết các bài toán liên quan một cách hiệu quả. Tuy nhiên, để thành thạo các bài toán về diện tích hình tròn, học sinh cần rèn luyện thường xuyên và linh hoạt trong cách áp dụng công thức.
Tổng hợp các cách tính chu vi hình chữ nhật kèm ví dụ minh họa dễ hiểu
Chu vi là đường bao quanh một hình, thể hiện độ dài của đường viền bao ngoài của hình đó. Đối với hình chữ nhật, chu vi được tính bằng tổng độ dài của bốn cạnh. Nắm vững kiến thức và cách tính chu vi hình chữ nhật chính xác có ý nghĩa quan trọng trong các ứng dụng thực tế như tính toán diện tích, thiết kế xây dựng..
Công thức tính thể tích hình trụ và các dạng bài tập thường gặp kèm lời giải chi tiết
Tính thể tích hình trụ là dạng bài tập đơn giản nhưng xuất hiện rất nhiều trong các đề thi và đề kiểm tra. Thể tích hình trụ được tính bằng công thức: V = Sđáy.h. Trong đó, Sđáy là diện tích mặt đáy, h là chiều cao của hình lăng trụ đó. Ứng dụng của hình trụ dễ thấy ở lĩnh vực xây dựng hay thiết kế sản phẩm.
Diện tích hình tam giác: Hướng dẫn tính toán chi tiết cho mọi trường hợp
Diện tích hình tam giác - một khái niệm toán học cơ bản nhưng lại vô cùng quan trọng và có ứng dụng rộng rãi trong thực tế. Nắm vững các công thức và kỹ thuật tính diện tích tam giác sẽ giúp bạn giải quyết dễ dàng các bài toán liên quan.
Công thức tính thể tích hình nón áp dụng với mọi dạng bài tập
Thể tích hình nón bằng 1/3 giá trị của π nhân với bình phương bán kính đáy mặt nón và nhân với chiều cao. Cụ thể, hình nón được tính thể tích bằng công thức V = 1/3.S.h = 1/3.π.r2.h. Trong đó, h là khoảng cách từ tâm mặt đáy đến đỉnh hình chóp và r là bán kính hình tròn đáy.