Mặt cầu là gì?
Mặt cầu và khối cầu là hai khái niệm toán học quan trọng trong hình học không gian, với nhiều ứng dụng trong thực tế. Hiểu rõ định nghĩa và tính chất của chúng giúp giải quyết các bài toán liên quan đến diện tích mặt hình cầu một cách hiệu quả.
Hãy tưởng tượng một quả bóng đá, bề mặt bên ngoài của quả bóng chính là mặt cầu. Mặt cầu được tạo thành bởi tất cả các điểm cách đều một điểm cố định gọi là tâm (O) một khoảng cách không đổi gọi là bán kính (r).
Khối cầu là tập hợp các điểm nằm bên trong mặt cầu. Khối cầu cũng được gọi là hình cầu.

Công thức tính diện tích mặt hình cầu
Diện tích mặt cầu là đại lượng đo lường tổng diện tích của bề mặt cong bao quanh khối cầu. Bề mặt cong này được hình thành bởi tập hợp các điểm cách đều một điểm cố định (tâm) một khoảng cách nhất định (bán kính).
Công thức tính diện tích bề mặt hình cầu
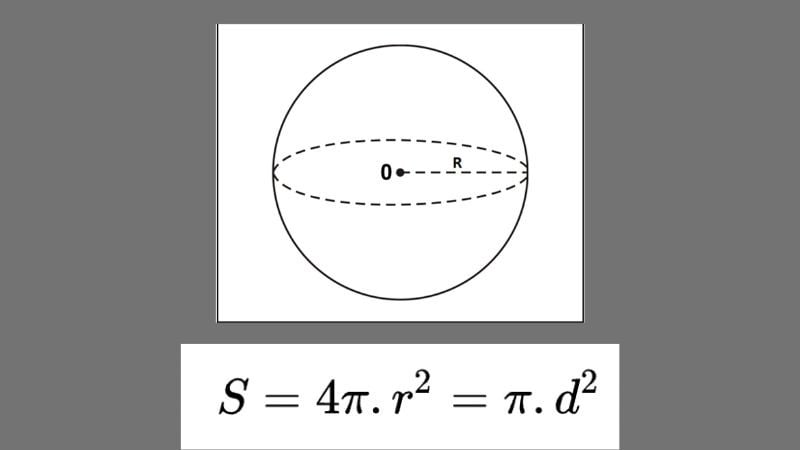
Diện tích mặt hình cầu được tính bằng công thức: S = 4πr², trong đó:
- S: Diện tích mặt cầu (đơn vị mét vuông, cm vuông,...)
- π: Hằng số Pi, xấp xỉ 3,14
- r: Bán kính mặt cầu (đơn vị mét, cm,...)
Ví dụ minh họa
Một quả bóng tennis có bán kính r = 3,2 cm. Diện tích mặt hình cầu của quả bóng này là:
S = 4πr² = 4π * 3,2² ≈ 131,2 cm²
Bài tập tính diện tích mặt cầu
Khi làm bài tập tính diện tích mặt cầu chúng ta có thể bắt gặp các dạng bài như sau:
Công thức tính bán kính mặt cầu
Công thức 1: Công thức tính bán kính mặt cầu ngoại tiếp khối chóp có cạnh bên vuông góc với đáy: R = √(Rd² + (h/2)²), trong đó:
- R: Bán kính mặt cầu ngoại tiếp (đơn vị mét, cm,...)
- Rd: Bán kính đường tròn ngoại tiếp đáy (đơn vị mét, cm,...)
- h: Chiều cao của hình chóp (đơn vị mét, cm,...)
Ví dụ: Cho hình chóp S.ABCD có đáy dạng hình chữ nhật. Độ dài AB = 3a, BC = 4a, SA = 12a và SA vuông góc với đáy. Tính bán kính R của mặt cầu ngoại tiếp hình chóp S.ABCD.
Lời giải:
ABCD là hình chữ nhật, ta có AC = √(AB² + BC²) = √((3a)² + (4a)²) = 5a.
Đường tròn ngoại tiếp hình chữ nhật ABCD có đường kính AC, do đó Rd = AC/2 = 5a/2.
SA vuông góc với đáy ABCD, do đó h = SA = 12a.
Áp dụng công thức:
R = √(Rd² + (h/2)²) = √((5a/2)² + (12a/2)²) = √(25a²/4 + 144a²/4) = √(169a²/4) = 13a/2.
Kết quả: Bán kính R của mặt cầu ngoại tiếp hình chóp S.ABCD là R = 13a/2.
Công thức 2: Công thức tính bán kính mặt cầu ngoại tiếp tứ diện vuông.
R = √(a^2+b^2+c^2)/2, trong đó: a,b,c là cạnh góc vuông.
Đây là trường hợp đặc biệt của công thức 1
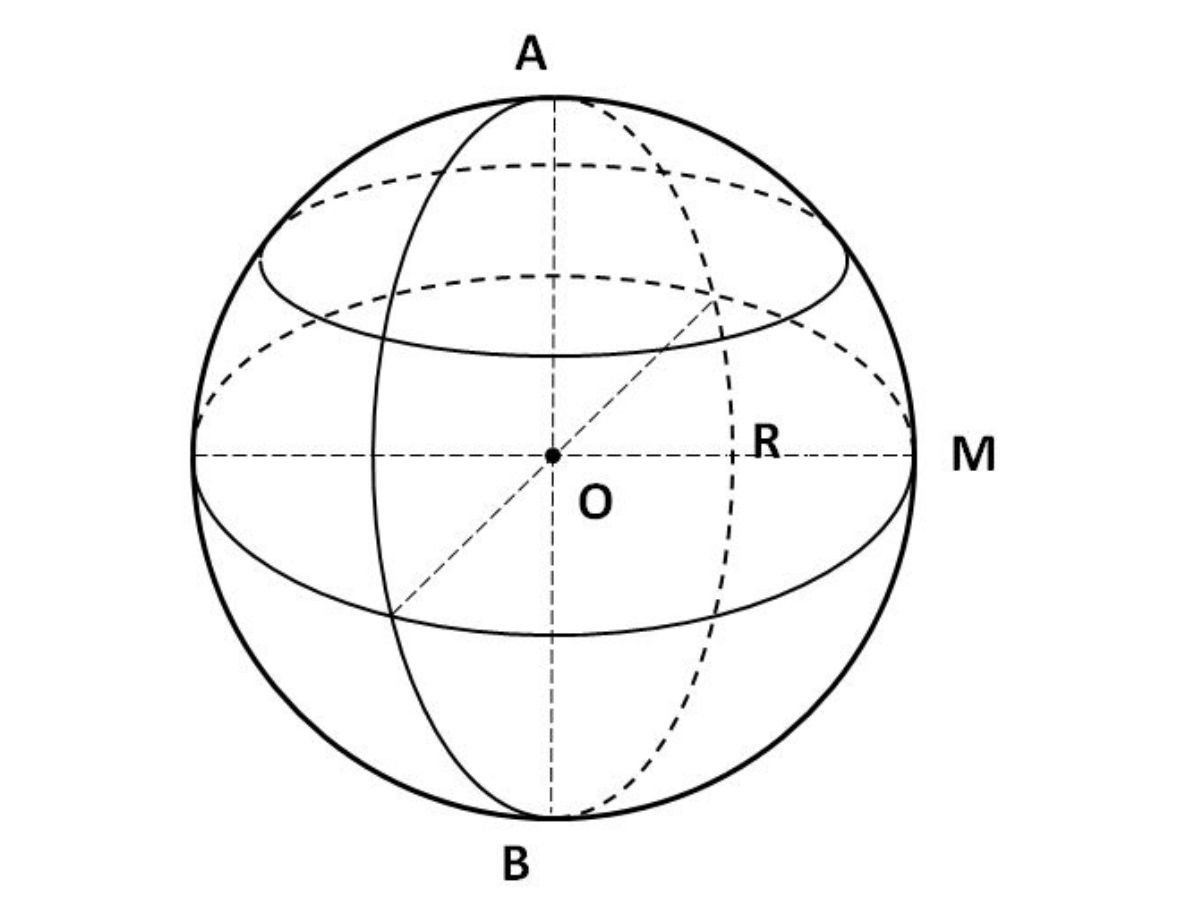
Tính diện tích mặt cầu bán kính r bằng bao nhiêu?
Câu 1: Một quả bóng tennis có bán kính 3,2 cm. Diện tích mặt hình cầu của quả bóng này là bao nhiêu?
Gợi ý giải:
Bán kính quả bóng tennis: r = 3,2 cm
Diện tích mặt cầu: S = 4πr² = 4π * 3,2² ≈ 131,2 cm²
Câu 2: Một bể chứa nước hình cầu có bán kính 1,5 m. Để sơn toàn bộ mặt ngoài của bể, cần bao nhiêu mét vuông sơn?
Gợi ý giải:
Diện tích mặt cầu: S = 4πr² = 4π * 1,5 m² ≈ 28,26 m²
Kết luận: Cần sơn 28,26 mét vuông sơn toàn bộ mặt ngoài của bể.
Câu 3: Một vệ tinh hình cầu có bán kính 200 km được phóng lên quỹ đạo Trái Đất. Diện tích mặt ngoài của vệ tinh này là bao nhiêu?
Gợi ý giải: Diện tích mặt cầu: S = 4πr² = 4π * 200.000² ≈ 1.600.000.000π m²
Câu 4: Một quả cầu kim loại có bán kính 4 cm được mạ vàng với độ dày 0,1 mm. Diện tích mặt vàng sau khi mạ tăng thêm bao nhiêu so với diện tích mặt hình cầu ban đầu?
Gợi ý giải:
Độ dày lớp mạ vàng: t = 0,1 mm = 0,001 cm
Bán kính sau khi mạ: r' = r + t = 4 cm + 0,001 cm = 4,001 cm
Diện tích mặt cầu ban đầu: S_ban đầu = 4π * 4² = 64π cm²
Diện tích mặt cầu sau khi mạ: S_mạ = 4π * 4,001² ≈ 64,08π cm²
Vậy diện tích tăng thêm: ΔS = S_mạ - S_ban đầu ≈ 64,08π cm² - 64π cm² ≈ 0,08π cm²
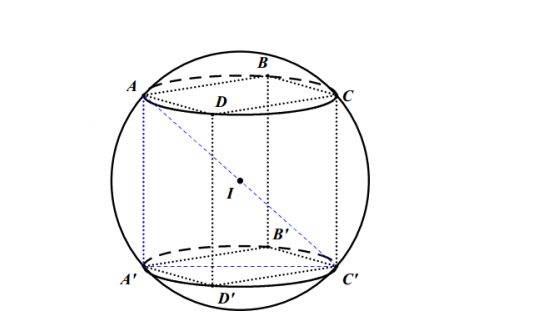
Cách tính diện tích mặt cầu ngoại tiếp hình hộp chữ nhật
Mặt cầu ngoại tiếp là mặt cầu tiếp xúc với tất cả các đỉnh của khối hộp chữ nhật. Bán kính mặt cầu bằng một nửa đường chéo không gian của khối hộp chữ nhật.
Bán kính mặt cầu ngoại tiếp:
Bán kính mặt cầu ngoại tiếp hình hộp chữ nhật bằng một nửa đường chéo của hình hộp chữ nhật đó.
Công thức: R = √(a² + b² + c²) / 2, trong đó:
R là bán kính mặt cầu ngoại tiếp.
a, b, c là ba kích thước của hình hộp chữ nhật (chiều dài, chiều rộng, chiều cao).
Diện tích mặt hình cầu ngoại tiếp được tính bằng công thức:
S = 4πR², trong đó:
- S là diện tích của mặt cầu ngoại tiếp.
- R là bán kính mặt cầu ngoại tiếp (đã tính ở bước 1).
Ví dụ: Cho một hình hộp chữ nhật có kích thước là 3 cm, 4 cm và 5 cm. Tính diện tích mặt cầu ngoại tiếp hình hộp chữ nhật nêu trên.
Giải:
Tính bán kính mặt cầu ngoại tiếp:
R = √(3² + 4² + 5²) / 2 = √50 / 2 = 5√2 / 2 cm
Tính diện tích mặt cầu ngoại tiếp:
S = 4π(5√2 / 2)² = 50π cm²
Vậy diện tích mặt cầu ngoại tiếp hình hộp chữ nhật này là 50π cm².
Cách tính mặt cầu ngoại tiếp khối chóp có cạnh bên vuông góc với đáy
Trước khi tính diện tích mặt hình cầu ngoại tiếp khối chóp có cạnh bên vuông góc với đáy ta cần tính bán kính của mặt cầu này với công thức như sau:
R = √(Rd² + (h/2)²)
- Rd là bán kính ngoại tiếp đáy.
- h: độ dài cạnh bên vuông góc với đáy.
Ví dụ: Cho hình chóp S.ABCD có đáy là hình chữ nhật với AB = 3, BC = 4, SA = 12 và SA vuông góc với đáy. Tính bán kính r của mặt cầu ngoại tiếp hình chóp tứ giác S.ABCD.
Theo công thức đã cho, ta có:
R = √(Rd² + (h/2)²)
R_đáy = AC/2 = √(AB² + CD²)/2 = 5/2 (vì AC là đường chéo dài của hình chữ nhật)
h = SA = 12a
Thay số vào công thức, ta dùng máy tính casio 580 online:
R = √((5/2)² + (12/2)²) = √(25/4 + 144/4) = √(169/4) = 13/2
Công thức tính bán kính mặt cầu cho khối chóp có mặt bên vuông góc đáy
Cho khối chóp S.A1A2...An có (SA1A2) ⊥ (A1A2...An). Đặt R1 là bán kính đường tròn ngoại tiếp tam giác S.A1A2, R2 là bán kính đường tròn ngoại tiếp đáy A1A2...An và GT là giao tuyến thì bán kính mặt cầu ngoại tiếp R của khối chóp S.A1A2...An được tính theo công thức:
R = √(R1² + R2² - GT²/4)
Ví dụ bài toán: Cho khối chóp S.ABC có (SAB) ⊥ (ABC). Trước khi tính diện tích mặt cầu ngoại tiếp hình chóp, hãy tìm tâm và bán kính mặt cầu ngoại tiếp khối chóp S.ABC.
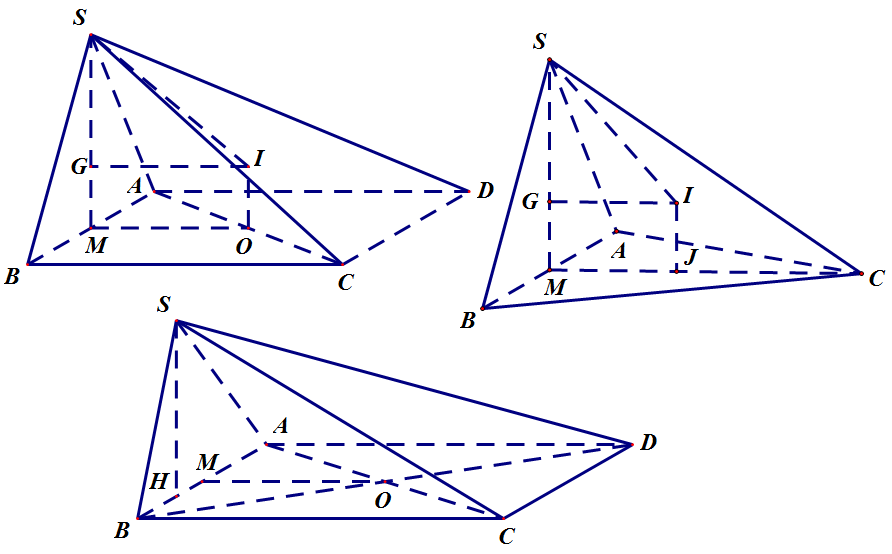
Phương pháp giải:
Đầu tiên ta xác định tâm mặt cầu:
Gọi O1, O2 lần lượt là tâm của đường tròn ngoại tiếp các tam giác ABC và SAB. Gọi E là trung điểm của cạnh AB.
Dựng đường thẳng d1 vuông góc với (ABC) qua O1, đường thẳng d2 vuông góc với (SAB) qua O2.
Gọi I là giao điểm của d1 và d2.
Chứng minh:
O1E ⊥ AB ⇒ O1E ⊥ (SAB) (do (SAB) ⊥ (ABC)).
O2E ⊥ AB ⇒ O1E ⊥ (ABC).
Do đó, I là giao điểm của ba đường vuông góc: (O1E, (ABC)), (O2E, (SAB)) và (AB).
Vậy I là tâm mặt cầu ngoại tiếp khối chóp S.ABC.
Tiếp theo, tính bán kính mặt cầu:
Tứ giác EO1IO2 là hình chữ nhật.
Do đó, IE² = O1E² + O2E².
Gọi R1, R2 lần lượt là bán kính đường tròn ngoại tiếp tam giác ABC, SAB.
Ta có:
O1E² = O1A² - EA² = R1² - AB²/4.
O2E² = O2A² - EA² = R2² - AB²/4.
Suy ra:
IE² = R1² + R2² - AB²/2.
R² = IE² + EA² = R1² + R2² - AB²/4.
Vậy bán kính mặt cầu ngoại tiếp R được tính theo công thức:
R = √(R1² + R2² - AB²/4)
Ví dụ minh họa: Cho hình chóp S.ABC có SA = a, tam giác ABC đều, tam giác SAB vuông cân tại S và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Tính bán kính mặt cầu ngoại tiếp hình chóp S.ABC nêu trên.
Đáp số: r = a√6/3
Ý nghĩa thực tiễn của diện tích hình cầu
Vai trò việc tính diện tích mặt hình cầu không chỉ giới hạn trong các bài toán học tập mà còn mở rộng sang nhiều lĩnh vực:
Kiến trúc và xây dựng:
- Tính toán diện tích bề mặt của các công trình hình cầu như mái vòm nhà hát, bể chứa nước hình cầu hoặc các cấu trúc nhà ở dạng mái vòm.
- Tính toán lượng ánh sáng hoặc âm thanh cần thiết để chiếu sáng hoặc khuếch đại âm thanh cho một không gian hình cầu.
Kỹ thuật:
- Thiết kế các thiết bị và bộ phận hình cầu như pin mặt trời, bóng đèn hoặc các bộ phận trong động cơ.
- Tính toán lực cản của chất lỏng (như nước hoặc không khí) tác động lên các vật thể hình cầu khi di chuyển trong môi trường đó.
Khoa học:
- Tính toán diện tích bề mặt của các hành tinh và vệ tinh trong hệ mặt trời, từ đó cung cấp thông tin về kích thước và cấu tạo của chúng.
- Mô phỏng các hiện tượng tự nhiên như sự lan truyền nhiệt, sự khuếch tán của các chất hoặc sự di chuyển của các hạt trong môi trường.

Mối liên kết giữa diện tích hình cầu và thể tích hình cầu
Diện tích mặt hình cầu: Bao phủ bề mặt cong của hình cầu, được tính bằng công thức S = 4πr², với r là bán kính.
Thể tích hình cầu: Thể hiện không gian chứa đựng bên trong hình cầu, được tính bằng công thức V = (4/3)πr³, cũng với r là bán kính.
Mối liên kết giữa diện tích mặt hình cầu và thể tích thể hiện sự khác biệt về cách thức gia tăng của hai đại lượng này khi kích thước hình cầu thay đổi. Thể tích hình cầu gấp 3 lần diện tích hình cầu có cùng bán kính.
Mối liên kết giữa diện tích và thể tích hình cầu tạo nền tảng cho việc nghiên cứu các hình dạng phức tạp hơn, góp phần thúc đẩy sự phát triển của hình học và các lĩnh vực liên quan.
Tại sao hành tinh và ngôi sao luôn hình cầu?
Lý do chính khiến hành tinh và ngôi sao luôn có hình cầu là do lực hấp dẫn. Khi một thiên thể có đủ khối lượng, lực hấp dẫn của nó sẽ kéo mọi vật chất về phía trung tâm của nó.
Ban đầu, các hành tinh và ngôi sao hình thành từ những đám mây bụi và khí khổng lồ. Dưới tác động của lực hấp dẫn, các hạt bụi và khí va chạm và kết dính với nhau, dần dần tạo thành những vật thể lớn hơn. Khi khối lượng của vật thể càng lớn, lực hấp dẫn càng mạnh, kéo vật thể về phía trung tâm nhiều hơn, khiến nó co lại và dẹp ra ở các cực.
Quá trình này diễn ra liên tục trong hàng triệu, thậm chí hàng tỷ năm, cho đến khi vật thể đạt được cân bằng thủy tĩnh học, nghĩa là lực hấp dẫn cân bằng với lực hướng tâm do chuyển động quay của nó.
Hình dạng hình cầu là hình dạng có diện tích bề mặt nhỏ nhất cho một thể tích nhất định. Điều này có nghĩa là nó giảm thiểu năng lượng hấp dẫn cần thiết để giữ vật thể lại với nhau. Do đó, đây là hình dạng ổn định nhất cho các thiên thể có khối lượng lớn.

Dạng bài tập tính diện tích mặt hình cầu là một dạng bài tập cơ bản và quan trọng trong chương trình học Toán. Việc nắm vững kiến thức và phương pháp giải dạng bài tập này giúp học sinh có thể ứng dụng vào thực tế và giải quyết các vấn đề liên quan đến hình cầu một cách hiệu quả.



























