Hình thang là gì?
Hình thang là một hình tứ giác chứa hai cạnh đối song song với nhau. Hai cạnh song song này được gọi là đáy lớn và đáy bé của hình thang. Hai cạnh còn lại được gọi là hai cạnh bên.
Hình thang cân cũng là hình thang nhưng có hai cạnh bên bằng nhau. Điều này có nghĩa là hai cạnh bên của hình thang cân có độ dài bằng nhau và các góc ở hai đáy cũng bằng nhau.
Hình thang vuông là hình thang với ít nhất một góc vuông. Điều này có nghĩa là một trong hai cạnh bên của hình thang vuông, vuông góc với một trong hai đáy.
Để nhận biết hình thang, ta có thể dựa vào các dấu hiệu sau:
- Hình tứ giác có chứa hai cạnh đối song song với nhau.
- Nếu hình thang có ít nhất một góc vuông thì hình thang đó là hình thang vuông.
- Nếu một hình thang có hai cạnh bên bằng nhau thì hình thang đó là hình thang cân.
- Nếu hai góc kề cùng một đáy của hình thang bằng nhau thì hình thang đó là hình thang cân.
- Nếu hai đường chéo của hình bằng nhau thì hình thang đó là hình thang cân.
- Nếu hai góc kề của cạnh đáy và cạnh bên của hình thang bằng nhau thì hình thang đó là hình thang cân.
- Nếu hai trục đối xứng của hai đáy của hình thang trùng nhau thì hình thang đó là hình thang cân.
- Nếu một hình thang nội tiếp đường tròn thì hình thang đó là hình thang cân.
Hình thang có những tính chất cơ bản sau đây giúp bạn phân biệt cách tính chu vi hình thang:
- Tổng hai góc kề một cạnh bên: Trong hình thang, tổng số đo hai góc kề một cạnh bên bất kỳ bằng 180 độ. Điều này có nghĩa là nếu hai góc kề cùng một cạnh bên, tổng của chúng luôn là một góc bẹt.
- Các đường chéo: Trong hình thang tổng quát, các đường chéo không bằng nhau và không chia đôi nhau.
- Trung điểm của các cạnh bên: Đường thẳng nối trung điểm của hai cạnh bên của hình thang song song với hai đáy và bằng nửa tổng độ dài của hai đáy. Đường thẳng này gọi là đường trung bình của hình thang.
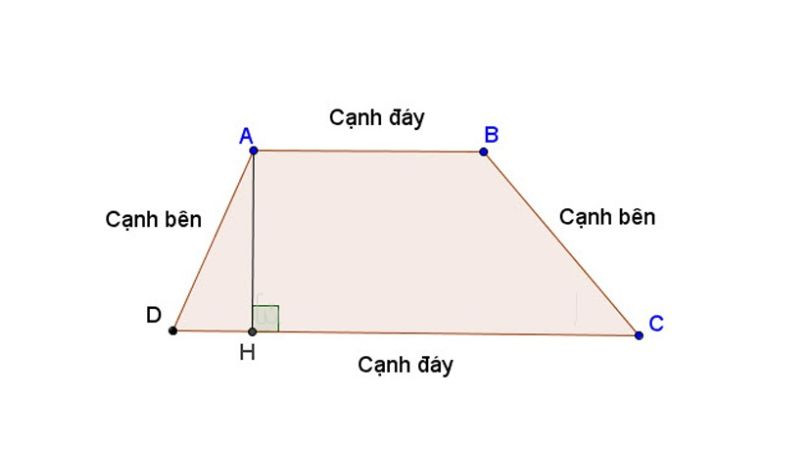
Công thức tính chu vi hình thang
Chu vi hình thang được định nghĩa là tổng độ dài của tất cả các cạnh của hình thang đó. Nó bao quanh toàn bộ hình dạng và thể hiện kích thước bên ngoài của hình thang.
Công thức tính chu vi hình thang bằng máy tính online phụ thuộc vào loại hình thang cụ thể:
Cách tính chu vi hình thang thường
Chu vi của hình thang được tính bằng tổng độ dài của tất cả các cạnh, bao gồm cả hai cạnh đáy và hai cạnh bên. Muốn tính chu vi hình thang, hãy áp dụng công thức đơn giản sau:
Công thức chung là: P = a + b + c + d
Trong đó:
- P là chu vi của hình thang
- a,b: độ dài của hai cạnh đáy
- c và d là độ dài của hai cạnh bên
Ví dụ: Cho hình thang MNPQ với độ dài các cạnh bên lần lượt là 10 cm và 12 cm, độ dài đáy lớn là 20 cm và độ dài đáy bé là 15 cm. Tính chu vi hình thang MNPQ.
Bài giải:
Chu vi của hình thang MNPQ là:
P=10+12+20+15=57 cm
P=10+12+20+15=57cm
Đáp số: 57 cm.
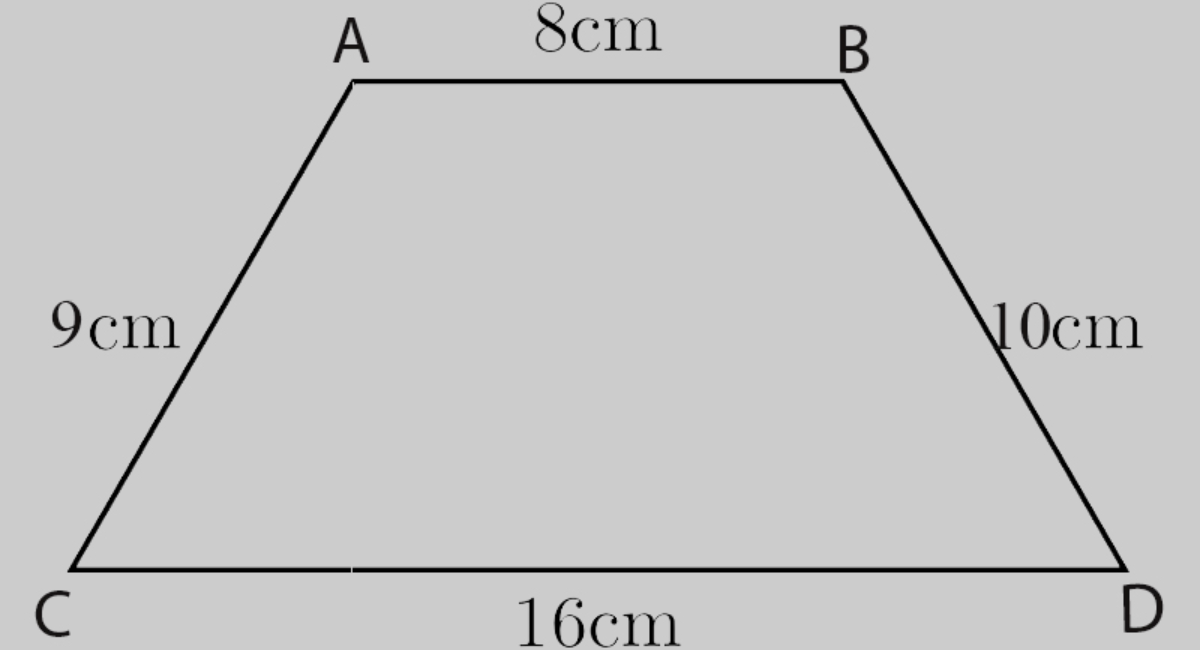
Cách tính chu vi hình thang cân
Đặc điểm nổi bật của hình thang cân là hai cạnh bên có độ dài bằng nhau nhưng không song song với nhau. Do cấu trúc đặc biệt này, công thức tính chu vi hình thang cân cũng có sự khác biệt so với hình thang thường.
Công thức riêng hình thang cân là: P = a + b + 2c
Trong đó:
- P là chu vi của hình thang cân
- a,b: độ dài của hai cạnh đáy
- c là độ dài của hai cạnh bên (vì hai cạnh bên bằng nhau)
Ví dụ: Cho hình thang cân EFGH với độ dài đáy lớn là 18 cm, độ dài đáy bé là 10 cm và độ dài hai cạnh bên đều là 7 cm. Tính chu vi hình thang EFGH.
Bài giải:
Chu vi của hình thang cân EFGH là:
P=18+10+2×7=18+10+14=42 cm
P=18+10+2×7=18+10+14=42cm
Đáp số: 42 cm.
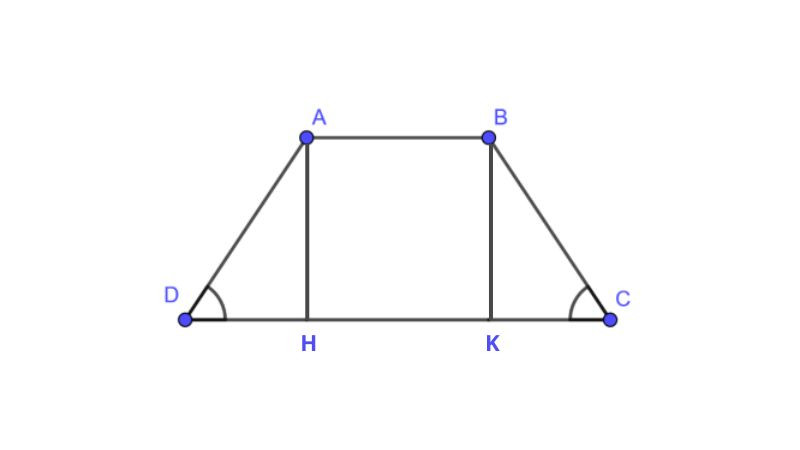
Chu vi hình thang vuông
Hình thang vuông là hình thang có một góc vuông, với cạnh bên vuông góc với hai đáy, đóng vai trò là chiều cao của hình. Cách tính chu vi của hình thang vuông cũng giống như cách tính chu vi của hình thang thông thường.
Công thức chung là: P = a + b + c + d
Trong đó:
- P: chu vi
- a, b: độ dài của hai cạnh đáy
- c và d là độ dài của hai cạnh bên
Ví dụ: Cho hình thang vuông với độ dài đáy lớn là 13 cm, đáy bé là 25 cm, và hai cạnh bên lần lượt là 12 cm và 18 cm. Tính chu vi hình thang.
Bài giải:
Chu vi của hình thang vuông KLMN là:
P=25+13+12+18=68 cm
Đáp số: 68 cm.
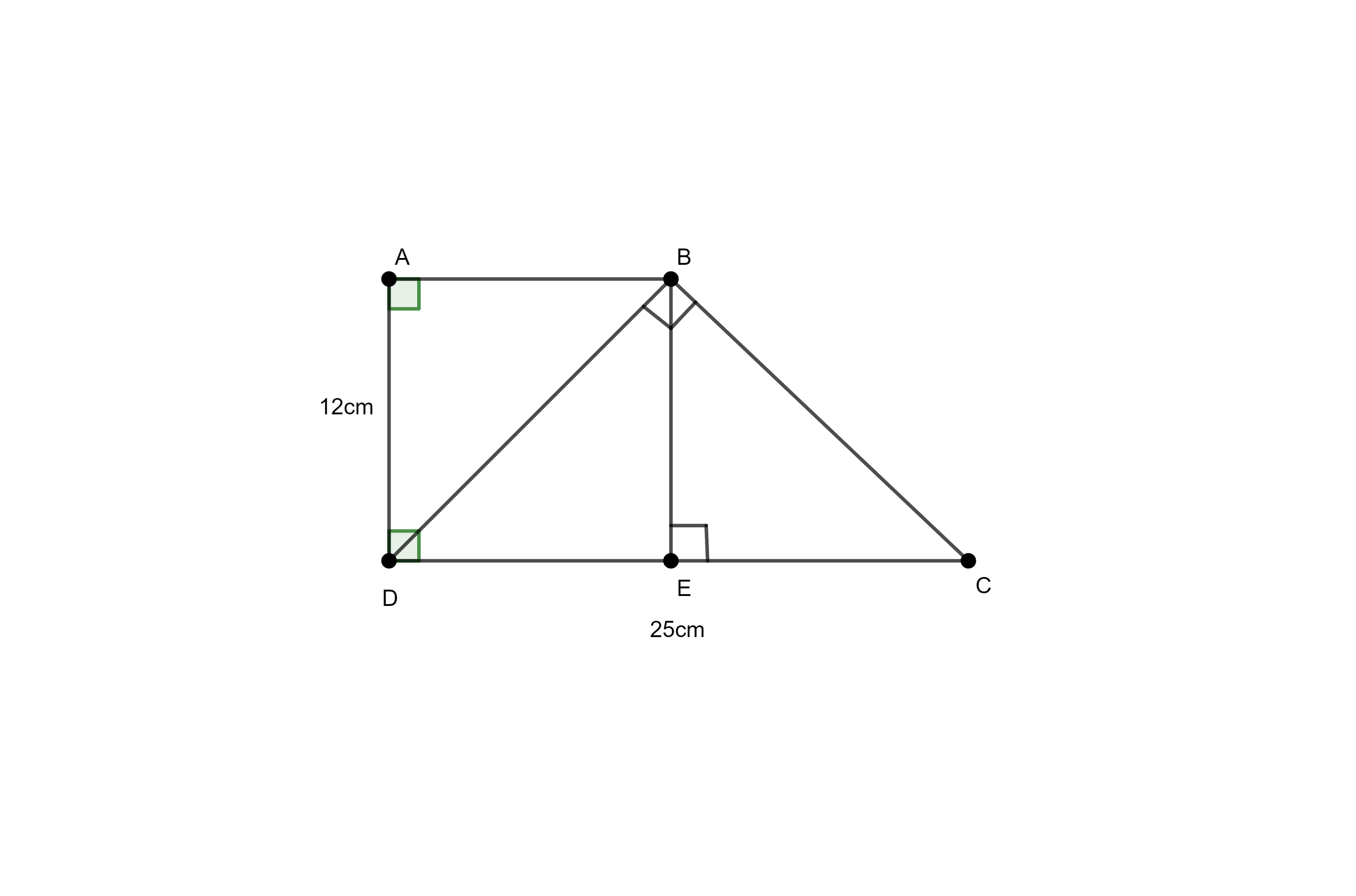
Các dạng bài tập về tính chu vi hình thang
Luyện tập thành thạo với các bài tập đa dạng, từ đơn giản đến nâng cao, giúp bạn tự tin giải quyết mọi vấn đề về chu vi hình thang.
Dạng 1: Tính chu vi hình thang khi biết độ dài các đáy và cạnh bên
Phương pháp giải: Áp dụng công thức tính chu vi hình thang để có được kết quả chính xác.
Công thức chung là: P = a + b + c + d (trong đó P là chu vi, a và b là độ dài hai cạnh đáy, c và d là độ dài hai cạnh bên)
Ví dụ: Cho hình thang ABCD với đáy lớn là 12 cm, đáy bé là 10 cm, và hai cạnh bên lần lượt là 7cm và 8 cm. Tính chu vi hình thang ABCD.
Lời giải:
Chu vi của hình thang ABCD là:
P= 12+10+7+8=37 cm
Đáp số: 37 cm
Dạng 2: Tính độ dài cạnh bên của hình thang cân khi biết chu vi
Phương pháp giải: Áp dụng công thức tính chu vi hình thang cân và dữ kiện đã cho để suy ra độ dài cạnh bên tương ứng.
Công thức chung là: P = a + b + 2c (trong đó P là chu vi, a và b là độ dài hai cạnh đáy, c là độ dài hai cạnh bên).
Ví dụ: Cho hình thang cân ABCD có chu vi là 68cm và độ dài hai cạnh đáy lần lượt là 20 cm và 26 cm. Tính độ dài cạnh bên của hình thang.
Lời giải:
Tổng độ dài hai cạnh bên của hình thang cân ABCD là:
68−20−26=22 cm
Độ dài của một cạnh bên là:
22: 2=11 cm
Đáp số: 11 cm
Dạng toán nâng cao
Bài 1: Một hình thang cân có chu vi là 54 cm, cạnh bên có chiều dài là 9cm và đáy dài gấp đôi đáy ngắn. Tính độ dài của đáy dài, đáy ngắn.
Lời giải:
Gọi đáy ngắn là X cm. Khi đó đáy dài là 2X cm.
Chu vi hình thang là:
X+2X+2 x 9=54
3X+18=54
3X=36
X=12
Đáp số: Đáy dài: 24 cm, Đáy ngắn: 12 cm
Bài 2: Hình thang có chu vi là 38 cm. Đáy dài là 12 cm và đáy ngắn là 8 cm. Hãy tính chiều cao của nó.
Lời giải:
Chu vi hình thang là:
P=a+b+c+d
38=12+8+c+c
38=12+8+c+d
Đáp số: Không xác định chiều cao từ chu vi nếu không biết rõ cạnh bên.
Bài 3: Cho biết chu vi hình thang cân là 38cm, cạnh bên dài lần lượt là 6cm và 7cm, đáy ngắn bằng một nửa đáy dài. Hãy tính chiều dài của đáy dài và đáy ngắn.
Lời giải:
Gọi đáy ngắn là X cm. Khi đó đáy dài là 2X cm.
Chu vi hình thang là:
X+2X+7+6=38
3X+13=38
3X=25
X=8.33
Đáp số: Đáy dài: 16.66 cm, Đáy ngắn: 8.33 cm
Bài 4: Cho hình thang cân có hai cạnh đáy lần lượt là 7cm và 5cm. Chiều dài của hai cạnh bên bằng một nửa tổng độ dài hai cạnh đáy. Tính chu vi hình thang đó, biết rằng hình thang có hai cạnh bên bằng nhau?
Lời giải:
Cạnh bên bằng một nửa tổng độ dài của hai cạnh đáy:
(7+5) : 2 = 6cm
Chu vi hình thang là:
P=7+5+6+6=24 cm
Đáp số: 24 cm
Mẹo ghi nhớ và quy luật của công thức tính chu vi hình thang
Quy luật cơ bản để tính chu vi của mọi hình là tổng độ dài của các cạnh và công thức tính cho hình thang cũng tương tự.
Hãy tưởng tượng hình thang như một mái nhà với hai phần mái chéo (cạnh bên) và hai phần tường (cạnh đáy). Chu vi hình thang chính là tổng độ dài của "vòng mái" và "vòng tường" của ngôi nhà.
Khi thực hiện tính toán, bạn cần chú ý đến đơn vị đo của các cạnh (đường cao, đáy dài, đáy ngắn và hai cạnh bên) để đảm bảo tính chính xác cho kết quả cuối cùng.
Bên cạnh đó, với việc thực hành và làm nhiều bài tập, bạn sẽ nắm vững cách áp dụng công thức tính chu vi của hình thang một cách hiệu quả.
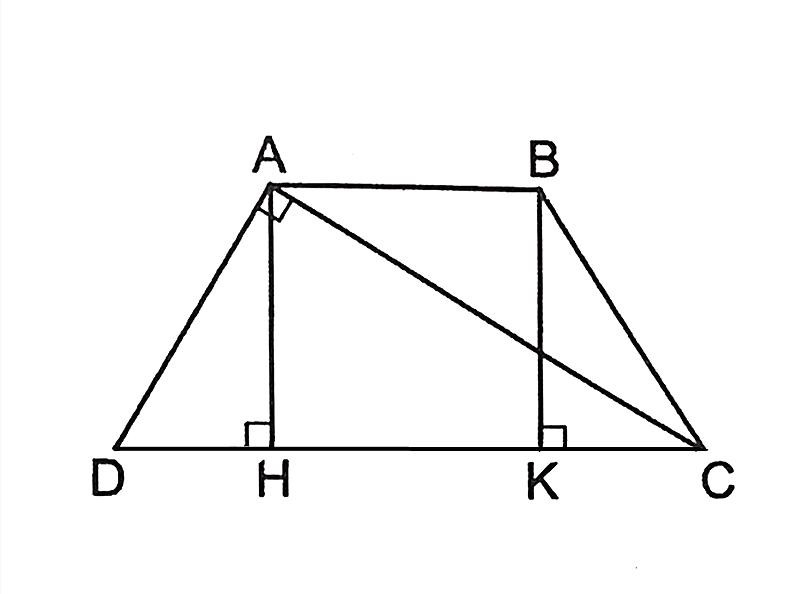
Tìm điều kiện để hình thang cân thành hình chữ nhật
Hình thang cân và hình chữ nhật đều là những tứ giác, tuy nhiên có một số đặc điểm khác nhau. Hình thang cân có hai góc kề một đáy bằng nhau, hai cạnh bên bằng nhau nhưng không song song. Hình chữ nhật có bốn góc vuông và hai cặp cạnh đối diện bằng nhau, song song với nhau.
Vậy, điều kiện để hình thang cân trở thành hình chữ nhật là:
Cách 1: Hình thang cân phải có ít nhất một góc vuông:
Nếu một trong hai góc kề đáy của hình thang cân bằng 90 độ thì hình thang đó tự động trở thành hình chữ nhật.
Ví dụ: Hình thang ABCD có AB // CD, Do ∠B và ∠C kề đáy nên nếu ∠B = 90 độ và ∠C cũng bằng 90 độ thì hình thang ABCD là hình chữ nhật.
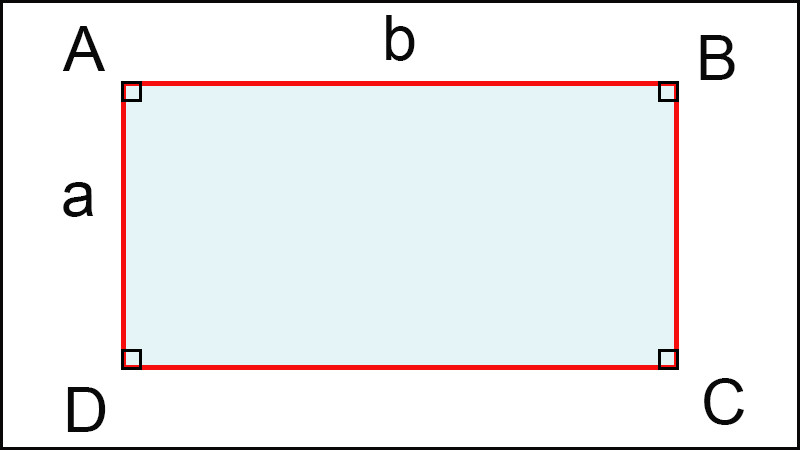
Cách 2: Hai cạnh đáy của hình thang cân phải bằng nhau:
Nếu hai cạnh đáy của hình thang cân bằng nhau thì khi có thêm một góc vuông, hai cạnh đáy sẽ trở thành hai cặp cạnh đối diện bằng nhau và song song với nhau, thỏa mãn điều kiện của hình chữ nhật.
Ví dụ: Hình thang ABCD có AB = CD, ∠B = 90 độ. Do ∠B và ∠C kề đáy nên ∠C cũng bằng 90 độ. Do đó, hình thang ABCD là hình chữ nhật.
Tính chu vi hình thang không chỉ đòi hỏi kiến thức cơ bản về hình học mà còn yêu cầu sự tỉ mỉ, logic và kiên nhẫn. Qua việc làm bài tập, chúng ta có thể rèn luyện kỹ năng tính toán, tăng cường khả năng phát triển logic và sự nhạy bén trong việc áp dụng kiến thức vào thực hành.



























