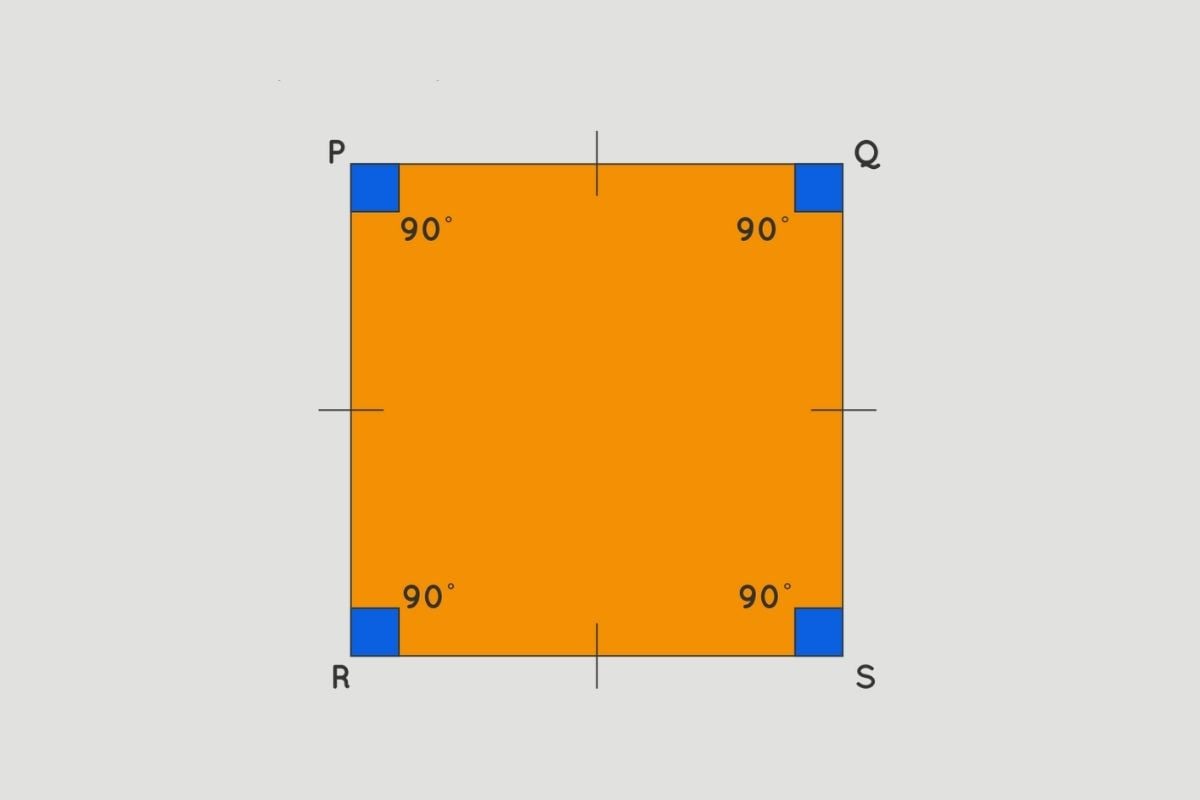
Khái niệm và các tính chất của hình vuông
Muốn tính chu vi hình vuông trước hết người học cần nẵm vững đây là tứ giác rất đặc biệt với đồng thời bốn cạnh bằng nhau và bốn góc vuông. Nói cách khác, hình vuông là hình thoi có bốn góc vuông.
Về các tính chất của hình vuông, ta có thể kể đến một số đặc điểm nổi bật sau:
- Đường chéo của hình vuông: d = a√2 (trong đó a là độ dài cạnh của hình vuông).
- Hai đường chéo vuông góc và chia nhau tại trung điểm của mỗi đường.
- Hình vuông có bốn trục đối xứng và bốn tâm đối xứng.
- Hình vuông là hình chữ nhật có tất cả các cạnh bằng nhau.
- Hình vuông là hình thoi có tất cả các góc bằng nhau.
Chu vi hình vuông là gì?
Chu vi hình vuông là tổng độ dài của bốn cạnh bằng nhau của hình vuông. Nói cách khác, nó là quãng đường bao quanh hình vuông. Chu vi hình vuông đóng vai trò quan trọng trong việc tính toán diện tích, xác định kích thước và ứng dụng trong thực tế.
Toàn bộ công thức tính chu vi hình vuông
Việc xác định chu vi hình vuông đóng vai trò quan trọng trong nhiều ứng dụng thực tế, chẳng hạn như tính toán diện tích, thiết kế hàng rào hay xác định chu vi của một khu đất hình vuông. Do đó, người học cần nắm chắc các công thức dưới đây.
Tìm chu vi khi biết độ dài một cạnh của hình vuông
Ở cấp tiểu học, muốn tính chu vi hình vuông lớp 3, 4 thì công thức đơn giản nhất là (C) = a + a + a + a = 4a, với a là độ dài của một cạnh hình vuông.
Ví dụ: Toán lớp 3 tính chu vi hình vuông đơn giản như sau: Cho một hình vuông có độ dài cạnh là 5cm. Áp dụng công thức, ta có chu vi hình vuông C = 4 * 5cm = 20cm
Tính chu vi khi biết diện tích
Công thức:
Diện tích S của hình vuông có thể tính bằng công thức: S = a²
Trong đó, a là độ dài một cạnh của hình vuông
Do đó, ta có thể lập ra mối liên hệ giữa chu vi P và diện tích S của hình vuông:
S = a² = (P/4)² = P² / 16
Từ đó, ta có thể suy ra công thức tính chu vi khi biết diện tích:
P = 4√S
Ví dụ: Cho một hình vuông có diện tích 25 cm². Hãy tìm chu vi của hình vuông đã cho.
Giải:
Áp dụng công thức, ta dùng máy tính online casio fx-580vn có:
P = 4√S = 4√25 cm² = 4 * 5 cm = 20 cm
Vậy chu vi của hình vuông đã cho là 20 cm.
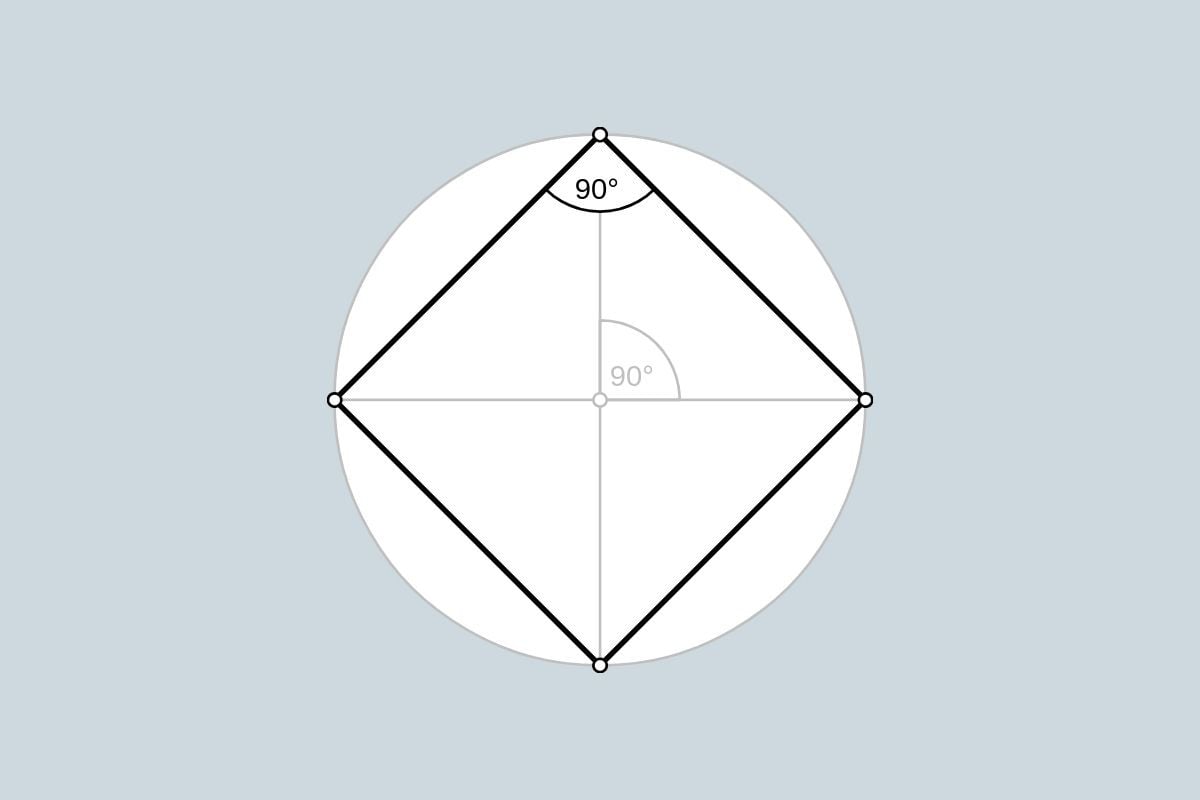
Tìm chu vi hình vuông nội tiếp trong một đường tròn
Công thức:
Chu vi P của hình vuông nội tiếp trong một đường tròn có bán kính r có thể tính bằng công thức:
P = 4r
Giải thích:
- Đường tròn có bán kính r có thể chia thành bốn phần bằng nhau bởi hai đường kính vuông góc.
- Mỗi phần của đường tròn là một tam giác vuông cân có cạnh huyền bằng đường kính và cạnh đáy bằng bán kính.
- Hình vuông nội tiếp trong đường tròn được tạo thành bởi bốn cạnh đáy của bốn tam giác vuông cân này.
- Do đó, chu vi P của hình vuông nội tiếp bằng 4 lần cạnh đáy, tức là 4 lần bán kính r của đường tròn.
Ví dụ: Cho một đường tròn có bán kính 4 cm. Hỏi hình vuông nội tiếp trong đường tròn đã nêu có chu vi bằng bao nhiêu?
Giải:
Áp dụng công thức, ta có:
P = 4r = 4 * 4 cm = 16 cm
Vậy chu vi của hình vuông nội tiếp trong đường tròn đó là 16 cm.
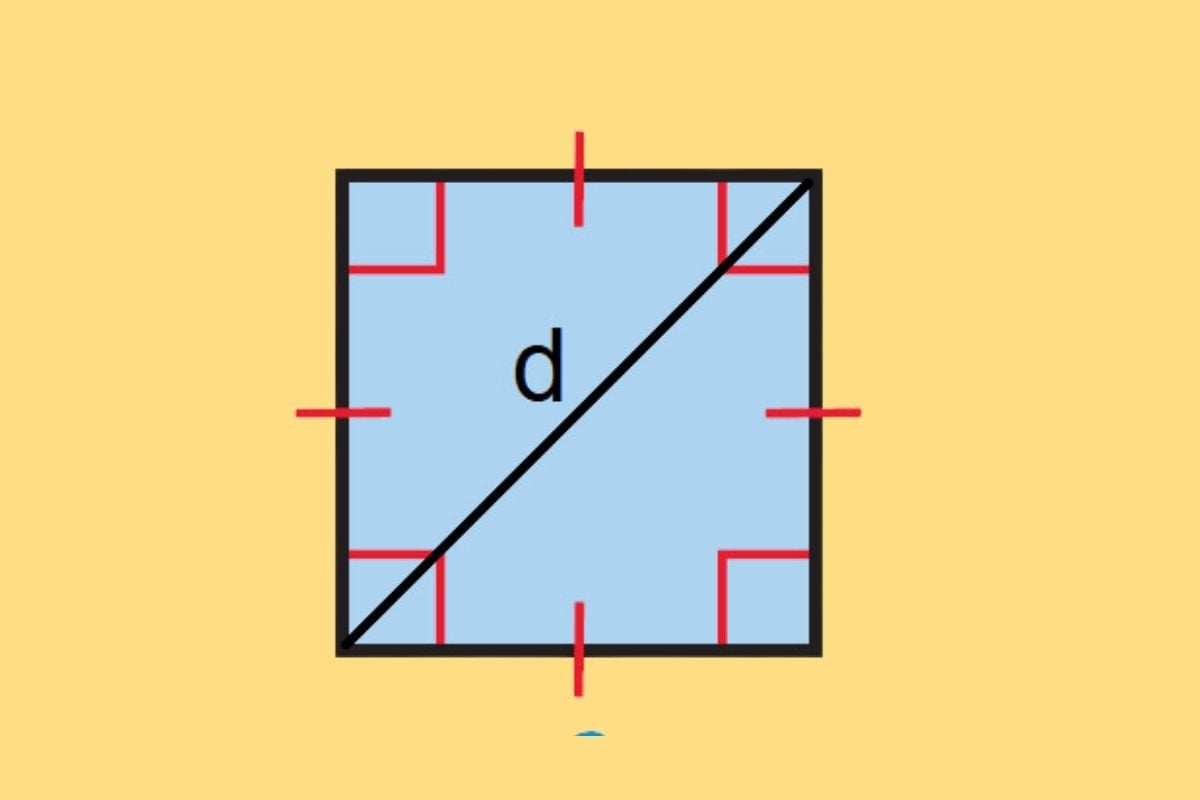
Tính chu vi hình vuông sử dụng đường chéo
Chu vi P của hình vuông có thể tính bằng công thức khi biết độ dài đường chéo d của hình vuông:
P = 4d / √2
Giải thích:
- Hình vuông và đường chéo:
- Hình vuông có bốn cạnh bằng nhau, được cắt nhau bởi hai đường chéo vuông góc tại tâm.
- Đường chéo d của hình vuông chia hình vuông thành hai tam giác vuông cân có:
- Cạnh huyền bằng đường chéo d
- Cạnh đáy bằng cạnh của hình vuông, kí hiệu là a
Áp dụng định lý Pythagore:
Gọi a là cạnh của hình vuông.
Xét một tam giác vuông cân tạo thành bởi đường chéo d và cạnh a của hình vuông.
Theo định lý Pythagore, ta có:
a² + a² = d²
Rút gọn và tìm chu vi:
Chuyển vế và ta được:
2a² = d²
Chia cả hai vế cho 2a^2:
1 = (d²) / (2a²)
Lấy căn bậc hai cho cả hai vế ta được:
√1 = √((d²) / (2a²))
Rút gọn:
a = d / √2
Thay a vào công thức tính chu vi P = 4a:
P = 4 * (d / √2)
Rút gọn:
P = 4d / √2
Vậy, công thức tính chu vi hình vuông khi biết đường chéo d là P = 4d / √2.
Ví dụ: Cho một hình vuông có đường chéo dài 8 cm. Tính chu vi của hình vuông đã cho.
Giải:
Áp dụng công thức, ta có:
P = 4d / √2 = 4 * 8 cm / √2 ≈ 22,66 cm
Vậy chu vi của hình vuông đó xấp xỉ 22,66 cm.
Bài tập thực hành về chu vi của một hình vuông
Một khu vườn hình vuông có chu vi là 20 m. Hỏi độ dài cạnh của khu vườn đã nêu bằng bao nhiêu?
Giải:
Gọi độ dài cạnh của khu vườn là a (m).
Áp dụng công thức tính chu vi của hình vuông, ta được:
Chu vi = 4a
Do đó, ta có phương trình:
20 = 4a
Giải phương trình, ta được:
a = 20 / 4 = 5
Vậy độ dài cạnh của khu vườn là 5 m.
Một mảnh đất hình vuông có diện tích là 64 m vuông. Hãy tính chu vi của mảnh đất đó.
Giải:
Gọi độ dài cạnh của mảnh đất là a (m).
Áp dụng công thức tính diện tích của hình vuông, ta có:
Diện tích = a²
Do đó, ta có phương trình:
64 = a²
Lấy căn bậc hai cho cả hai vế:
a = √64 = 8
Vậy độ dài cạnh của mảnh đất là 8 m.
Chu vi của mảnh đất đó là:
Chu vi = 4a = 4 * 8 = 32
Vậy chu vi của mảnh đất đó là 32 m.

Một tấm bìa hình vuông có đường chéo dài 10 cm. Hãy tìm chu vi của tấm bìa đã nêu.
Giải:
Gọi độ dài cạnh của tấm bìa là a (cm).
Đường chéo = a√2
Do đó, ta có phương trình:
10 = a√2
Chia cả hai vế cho √2, ta được:
a = 10 / √2
Rút gọn:
a = 10√2 / 2 = 5√2
Vậy độ dài cạnh của tấm bìa là 5√2 cm.
Chu vi của tấm bìa đó là:
Chu vi = 4a = 4 * 5√2 = 20√2
Vậy chu vi của tấm bìa đó là 20√2 cm.
Một khu vườn hình vuông có chu vi là 120m. Người ta muốn rào xung quanh khu vườn bằng những viên gạch có chiều dài 20cm. Hỏi cần bao nhiêu viên gạch để rào được cả khu vườn?
Giải:
Cạnh của khu vườn là: 120m / 4 = 30m
Số lượng viên gạch cần dùng là: 30m / 0,2m = 150 viên
Trên một mảnh đất hình vuông, người ta xây dựng một bồn hoa hình vuông ở chính giữa. Diện tích bồn hoa bằng 1/9 diện tích mảnh đất. Chu vi của mảnh đất là 80m. Tính cạnh của mảnh đất và cạnh của bồn hoa.
Giải:
Cạnh của mảnh đất là: 80m / 4 = 20m
Diện tích mảnh đất là: 20m x 20m = 400m²
Diện tích bồn hoa là: 400m² x 1/9 = 44,44m²
Cạnh của bồn hoa là: √44,44m² = 6,67m
Một khu đất hình vuông có chu vi là 240m. Người ta muốn chia khu đất thành 16 ô vuông nhỏ bằng nhau. Hỏi cạnh của mỗi ô vuông nhỏ là bao nhiêu mét?
Giải:
Cạnh của khu đất là: 240m / 4 = 60m
Cạnh của mỗi ô vuông nhỏ là: √(60m / 16) = 3,75m
Một khu đất hình vuông được bao quanh bởi một hàng rào. Biết rằng chu vi của khu đất là 40 m và chi phí để xây dựng hàng rào là 20.000 đồng/m. Hãy tính tổng chi phí xây dựng hàng rào cho khu đất đó.
Giải:
Gọi độ dài cạnh của khu đất là a (m).
Chu vi = 4a = 40
Giải phương trình, ta được:
a = 40 / 4 = 10
Vậy độ dài cạnh của khu đất là 10 m.
Chiều dài của hàng rào bằng chu vi của khu đất, tức là 40 m.
Tổng chi phí xây dựng hàng rào là:
Tổng chi phí = Chiều dài hàng rào * Giá xây dựng/m = 40 m * 20.000 đồng/m = 800.000 đồng
Vậy tổng chi phí xây dựng hàng rào cho khu đất đó là 800.000 đồng.
Một mảnh đất hình vuông có chu vi là 60m. Người ta muốn trồng cây xung quanh rìa mảnh đất với khoảng cách giữa các cây là 1m. Hỏi cần mua bao nhiêu cây giống để trồng?
Giải:
Cạnh của mảnh đất là: 60m / 4 = 15m
Chu vi phần đất trồng cây là: (15m - 1m) x 4 = 56m
Số lượng cây cần mua là: 56m / 1m = 56 cây

Câu hỏi thường gặp
Khi tìm hiểu công thức tính chu vi hình vuông cũng có một số thắc mắc của học sinh được đặt ra. Dưới đây là giải đáp chi tiết.
Làm thế nào để tìm chu vi của một hình vuông?
Để tính chu vi hình vuông, hãy cộng tất cả các cạnh của nó. Lưu ý, 4 cạnh của một hình vuông có chiều dài bằng nhau. Tổng các cạnh sẽ là chu vi của nó. Chúng ta cũng có thể sử dụng cách tìm chu vi hình vuông nếu biết chiều dài đường chéo hoặc diện tích hình vuông.
Đơn vị tính chu vi hình vuông là gì?
Chu vi hình vuông là tổng khoảng cách được bao quanh bởi các cạnh của nó. Chu vi được đo bằng các đơn vị như m (m), centimet (cm), decimet (dm),...
Diện tích hình vuông là gì?
Diện tích hình vuông là diện tích mà hình vuông bao phủ trong không gian hai chiều. Diện tích của hình vuông cũng có thể được định nghĩa là số đơn vị hình vuông cần thiết để lấp đầy hình vuông.
Hình vuông có mối liên hệ đặc biệt nào với các con số và phép toán?
Dãy số Fibonacci có thể được biểu diễn bằng các hình vuông liên tiếp, mỗi hình vuông có cạnh bằng tổng hai hình vuông trước đó.
Hình vuông có ứng dụng như thế nào trong thực tế?
Hình vuông hiện diện vô cùng phong phú xung quanh chúng ta:
- Kiến trúc: Cửa sổ, cửa ra vào, gạch ốp lát, mái nhà,... thường có hình vuông để tạo sự vuông vắn, chắc chắn và thẩm mỹ.
- Biểu tượng và logo: Nhiều thương hiệu nổi tiếng sử dụng logo hình vuông để thể hiện sự ổn định, tin cậy và chuyên nghiệp.
- Cờ Tướng: Bàn cờ Tướng được chia thành 64 ô vuông, nơi diễn ra các trận chiến trí tuệ đầy gay cấn.
- Rubik: Khối Rubik huyền thoại với 6 mặt vuông đầy màu sắc, thách thức trí thông minh và sự kiên nhẫn của người chơi.
Trên đây là toàn bộ kiến thức cần nắm được để vận dụng giải nhanh các bài toán liên quan đến chu vi hình vuông. Ngoài việc học thuộc công thức, người học cần thực hành qua nhiều dạng bài tập khác nhau để nâng cao trình độ, đồng thời nhớ lâu hơn.



























