Hình thoi là gì?
Để tính chu vi hình thoi, trước hết chúng ta cần hiểu rõ khái niệm và các tính chất hình học của nó. Hình thoi là một tứ giác đặc biệt sở hữu bốn cạnh bằng nhau cùng hai đường chéo vuông góc tại trung điểm của mỗi đường.
Có thể phân biệt hình thoi với các tứ giác khác như sau:
- Hình bình hành: Hình thoi là một loại hình bình hành đặc biệt với hai cạnh kề bằng nhau và hai đường chéo vuông góc.
- Hình chữ nhật: Hình thoi không có góc vuông, do đó không thể là hình chữ nhật.
- Hình vuông: Hình thoi có bốn cạnh bằng nhau nhưng hai đường chéo không nhất thiết bằng nhau (trừ trường hợp hình thoi là hình vuông).
Đặc điểm của hình thoi
Hình thoi có những tính chất riêng giúp chúng ta nhận biết và áp dụng trong việc tính toán hoặc phân tích hình học.
- Hình thoi có đầy đủ tất cả các tính chất giống như hình bình hành.
- Bốn cạnh luôn bằng nhau.
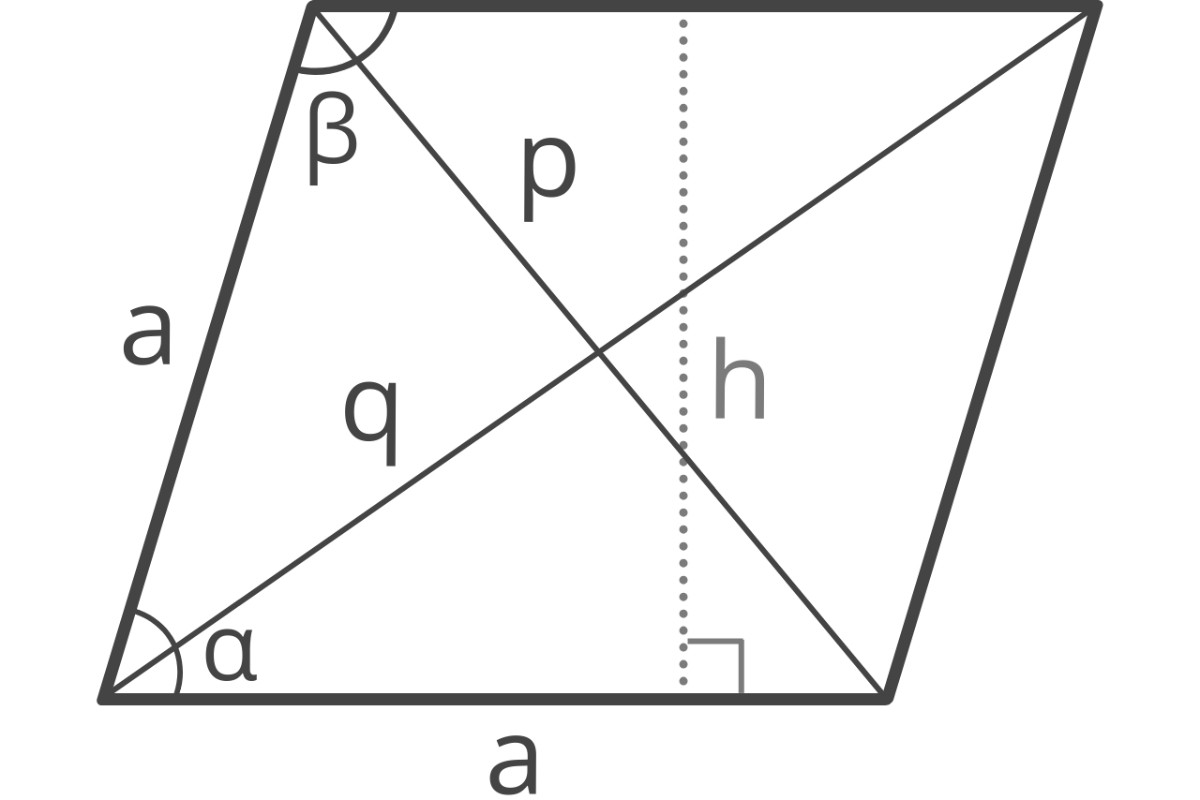
- Hai đường chéo vuông góc nhau tại trung điểm: O là giao điểm của AC và BD, đồng thời là trung điểm của mỗi đường chéo.
- Góc đối bằng nhau: ∠A = ∠C và ∠B = ∠D.
- Có bốn góc nhọn hoặc bốn góc tù.
- Tổng của hai góc kề nhau bất kỳ là 180°.
- Mỗi đường chéo của hình thoi đồng thời là đường phân giác của góc mà nó đi qua.
Công thức tính chu vi hình thoi
Chu vi thực chất là tổng độ dài của các cạnh tạo nên hình đó. Để tính chu vi hình thoi, học sinh có thể áp dụng linh hoạt các công thức dưới đây cho từng trường hợp.
Công thức cơ bản
Chu vi hình thoi (C) bằng tổng độ dài bốn cạnh của hình thoi:
C = 4a
Trong đó:
a là độ dài một cạnh của hình thoi.
Như vậy, chỉ cần biết độ dài một cạnh, bạn có thể dễ dàng xác định chu vi của hình thoi.
Ví dụ: Một hình thoi có cạnh dài 5cm. Tính chu vi của hình thoi đã nêu.
Giải:
a = 5cm
C = 4a = 4 * 5 = 20cm
Vậy chu vi hình thoi là 20cm.
Công thức tính chu vi hình thoi khi biết độ dài hai đường chéo
Khi biết độ dài hai đường chéo của hình thoi (d1, d2), công thức sau sẽ giúp bạn tính chu vi (C):
C = 2√(d1² + d2²)
Công thức này dựa trên định lý Pythagoras, liên hệ giữa độ dài các cạnh trong tam giác vuông.
Ví dụ: Hai đường chéo của một hình thoi có độ dài lần lượt là 6cm và 8cm. Tính chu vi của hình thoi đó.
Giải:
d1 = 6cm, d2 = 8cm
C = 2√(d1² + d2²) = 2√(6² + 8²) = 2√100 = 20cm
Vậy chu vi hình thoi là 20cm.
Công thức tính chu vi khi biết diện tích S
Nếu bạn biết diện tích (S) của hình thoi, hãy sử dụng công thức sau để tính chu vi (C):
C = 4√(S/2)
Công thức này dựa trên mối liên hệ giữa diện tích và độ dài cạnh của hình thoi.
Ví dụ: Một hình thoi có diện tích là 25cm². Tính chu vi của hình thoi này.
Giải:
S = 25cm²
C = 4√(S/2) = 4√(25/2) = 4√12.5 ≈ 20cm
Vậy chu vi hình thoi là 20cm (xấp xỉ).
Công thức tính chu vi khi biết góc
Trong trường hợp hiếm gặp khi bạn biết góc giữa hai cạnh kề nhau (θ) và độ dài một cạnh (a) của hình thoi, công thức sau sẽ giúp bạn tính chu vi (C):
C = 4a / sin(θ/2)
Công thức này dựa trên định lý sin trong tam giác, liên hệ giữa góc và độ dài cạnh trong tam giác.
Ví dụ: Một hình thoi có góc giữa hai cạnh kề nhau là 60° và độ dài cạnh là 4cm. Áp dụng công thức, ta có: Chu vi hình thoi = 4 * 4cm / sin 60° ≈ 11,5cm.

Cách tính độ dài các các cạnh hình thoi
Ngoài bài toán tính chu vi hình thoi đơn thuần, học sinh có thể bắt gặp những dạng bài tập đòi hỏi suy luận hơn như tính độ dài cạnh hình thoi khi được cung cấp một số dữ kiện đặc biệt.
Tìm độ dài cạnh khi biết chu vi
Công thức cơ bản để tính độ dài cạnh hình thoi dựa vào chu vi (P) là:
Độ dài cạnh (a) = Chu vi hình thoi (P) / 4
Ví dụ: Hình thoi ABCD có chu vi bằng 24cm. Tính độ dài cạnh a của hình thoi ABCD.
Giải:
Áp dụng công thức trên, ta có:
Độ dài cạnh a = (P) / 4 = 24cm / 4 = 6cm
Vậy độ dài cạnh a của hình thoi ABCD là 6cm.
Tìm độ dài cạnh khi biết độ dài hai đường chéo
Công thức:
a = 1/2 * √(d1² + d2²)
Tìm độ dài cạnh khi biết diện tích và độ dài một đường chéo
a = d1 * d2 / 2
Ví dụ: Một hình thoi có độ dài hai đường chéo lần lượt là 8cm và 6cm. Tính độ dài cạnh và diện tích của hình thoi đó.
Giải:
Độ dài cạnh a của hình thoi là:
a = 8 * 6 / 2 = 24 cm
Diện tích S của hình thoi là:
S = 8 * 6 / 2 = 24 cm²
Tính độ dài cạnh hình thoi khi biết góc giữa hai cạnh kề nhau θ và một cạnh a
Công thức
a = 2b/sin θ
Ví dụ: Một hình thoi có góc giữa hai cạnh kề nhau là 60° và độ dài đường phân giác trong góc đó là 3cm.
Giải:
Áp dụng công thức, ta có: a = 2 * 3cm / sin 60° ≈ 3,5cm.
Bài tập ứng dụng có lời giải chi tiết
Một hình thoi có cạnh dài 4cm. Hãy tính xem chu vi của hình thoi đó là bao nhiêu?
Giải:
Áp dụng công thức chu vi cơ bản: C = 4a = 4 * 4 = 16cm.
Vậy chu vi của hình thoi này là 16cm.
Hai đường chéo của một hình thoi có độ dài lần lượt là 3cm và 5cm. Hãy cho biết chu vi của hình thoi được nói đến.
Áp dụng công thức tính chu vi tính toán bằng máy tính online khi biết độ dài hai đường chéo: C = 2√(d1² + d2²) = 2√(3² + 5²) = 2√34 ≈ 10.8cm.
Vậy chu vi hình thoi là 10.8cm
Một hình thoi có diện tích là 25cm². Hỏi chu vi của hình thoi này là bao nhiêu?
Áp dụng công thức tính chu vi khi biết diện tích: C = 4√(S/2) = 4√(25/2) = 4√12.5 ≈ 20cm.
Vậy chu vi hình thoi là 20cm
Một mảnh đất hình thoi có chu vi là 40m. Tìm độ dài các cạnh của mảnh đất được nêu.
Gọi độ dài cạnh hình thoi là a.
Chu vi hình thoi: C = 4a = 40m.
Suy ra: a = C/4 = 40m/4 = 10m.
Vậy độ dài cạnh của mảnh đất là 10m.
Một mảnh đất hình thoi có độ dài hai đường chéo lần lượt là 16m và 20m. Người ta muốn rào xung quanh mảnh đất bằng 4 đường dây thép gai. Hỏi cần bao nhiêu m dây thép gai để rào mảnh đất?
Giải:
Vì chu vi của hình thoi bằng tổng độ dài bốn cạnh.
Áp dụng công thức tính, ta có:
Chu vi = 1/2 * d1 * d2 = 1/2 * 16 * 20 = 160 (m)
Vậy cần 160 m dây thép gai để rào mảnh đất.
Một khu vườn hình thoi có diện tích 48m². Biết độ dài đường chéo thứ nhất bằng 12m. Tính độ dài đường chéo thứ hai và chu vi của khu vườn.
Giải:
Áp dụng công thức tính diện tích của hình thoi, ta có:
Diện tích = 1/2 * d1 * d2 = 48
Giải phương trình: d2 = 48 / d1 = 48 / 12 = 4 (m)
Vậy độ dài đường chéo thứ hai là 4 m.
Chu vi hình thoi = 2 * (d1 + d2) = 2 * (12 + 4) = 32 (m)
Một hình thoi có chu vi bằng chu vi hình vuông có cạnh dài 8cm. Biết độ dài đường chéo thứ nhất của hình thoi là 6cm. Tính độ dài đường chéo thứ hai và diện tích của hình thoi.
Giải:
Chu vi hình vuông = cạnh * 4 = 8 * 4 = 32 (cm)
Vì chu vi hình thoi bằng chu vi hình vuông nên bằng 32 (cm)
Áp dụng công thức tính, ta có:
Chu vi = 2 * (d1 + d2) = 32
Giải phương trình: d2 = 32 - d1 = 32 - 6 = 26 (cm)
Vậy độ dài đường chéo thứ hai là 26 cm.
Diện tích hình thoi = 1/2 * d1 * d2 = 1/2 * 6 * 26 = 78 (cm²)
Một mảnh vải hình thoi có độ dài hai đường chéo lần lượt là 15dm và 20dm. Người ta cắt mảnh vải thành 4 mảnh vải hình vuông nhỏ bằng nhau. Tính diện tích mỗi mảnh vải hình vuông.
Giải:
Diện tích hình thoi = 1/2 * d1 * d2 = 1/2 * 15 * 20 = 150 (dm²)
Diện tích mỗi mảnh vải hình vuông = Diện tích hình thoi / 4 = 150 / 4 = 37,5 (dm²)
Một khu đất hình thoi có độ dài hai đường chéo lần lượt là 25m và 30m. Người ta muốn trồng hoa trên 3/5 diện tích khu đất. Hỏi cần bao nhiêu m vuông đất để trồng hoa?
Giải:
Diện tích hình thoi = 1/2 * d1 * d2 = 1/2 * 25 * 30 = 375 (m²)
Diện tích đất trồng hoa = 3/5 * Diện tích hình thoi = 3/5 * 375 = 225 (m²)
Một hình thoi có diện tích là 64cm² và hai đường chéo vuông góc với nhau tại O. Biết điểm O chia đường chéo AC thành hai đoạn AM và MC có độ dài lần lượt là 4cm và 10cm. Tính chu vi của hình thoi đang được nhắc đến.
Giải:
Áp dụng định lý Pythagoras vào tam giác AOM vuông góc tại O:
AM² + OM² = AO²
Thay số: 4² + OM² = (10/2)²
Giải phương trình: OM² = 36 - 25 = 11
Tính OM = √11 ≈ 3.3cm.
Áp dụng định lý Pythagoras vào tam giác COM vuông góc tại O:
CM² + OM² = CO²
Thay số: 10² + 3.3² = CO²
Giải phương trình: CO² = 113.31 ≈ 113.3cm
Tính CO = √113.3 ≈ 10.6cm.
Áp dụng công thức tính diện tích hình thoi: S = 1/2 * AC * BD = 1/2 * (AM + CM) * (CO + CO)
Thay số: S = 1/2 * (4 + 10) * (10.6 + 10.6) ≈ 25cm² (đúng với giả thiết).
Tính độ dài đường chéo BD: BD = 2 * CO ≈ 21.2cm.
Áp dụng công thức tính chu vi khi biết độ dài hai đường chéo: C = 2√(d1² + d2²) = 2√(10.6² + 21.2²) ≈ 63.2cm.
Vậy chu vi hình thoi là 63.2cm.

Cho một hình thoi có chu vi là 24cm. Biết độ dài đường chéo ngắn là 6cm. Tính độ dài đường chéo dài.
Giải:
Gọi độ dài đường chéo dài là x (cm).
Theo công thức tính chu vi dựa vào đường chéo, ta có:
24 = 2√(6² + x²)
12 = √(6² + x²)
144 = 6² + x²
x² = 144 - 36
x² = 108
x = √108 ≈ 10.39cm
Vậy độ dài đường chéo dài của hình thoi là 10.39cm.
Với những công thức và cách tính chi tiết được trình bày trên đây, hy vọng bạn đã có thể chinh phục các dạng bài tập liên quan đến chu vi hình thoi một cách thành thạo và nhanh chóng.



























