Lý thuyết liên quan đến hình chóp nón
Để giải quyết các bài tập liên quan đến diện tích toàn phần hình chóp nón, bạn cần phải hiểu bản chất của dạng hình học này. Mặc dù trong toán học chưa có định nghĩa chính thức về hình nón, ta có thể dựa vào thực tế để đưa ra một số cách hiểu như sau:
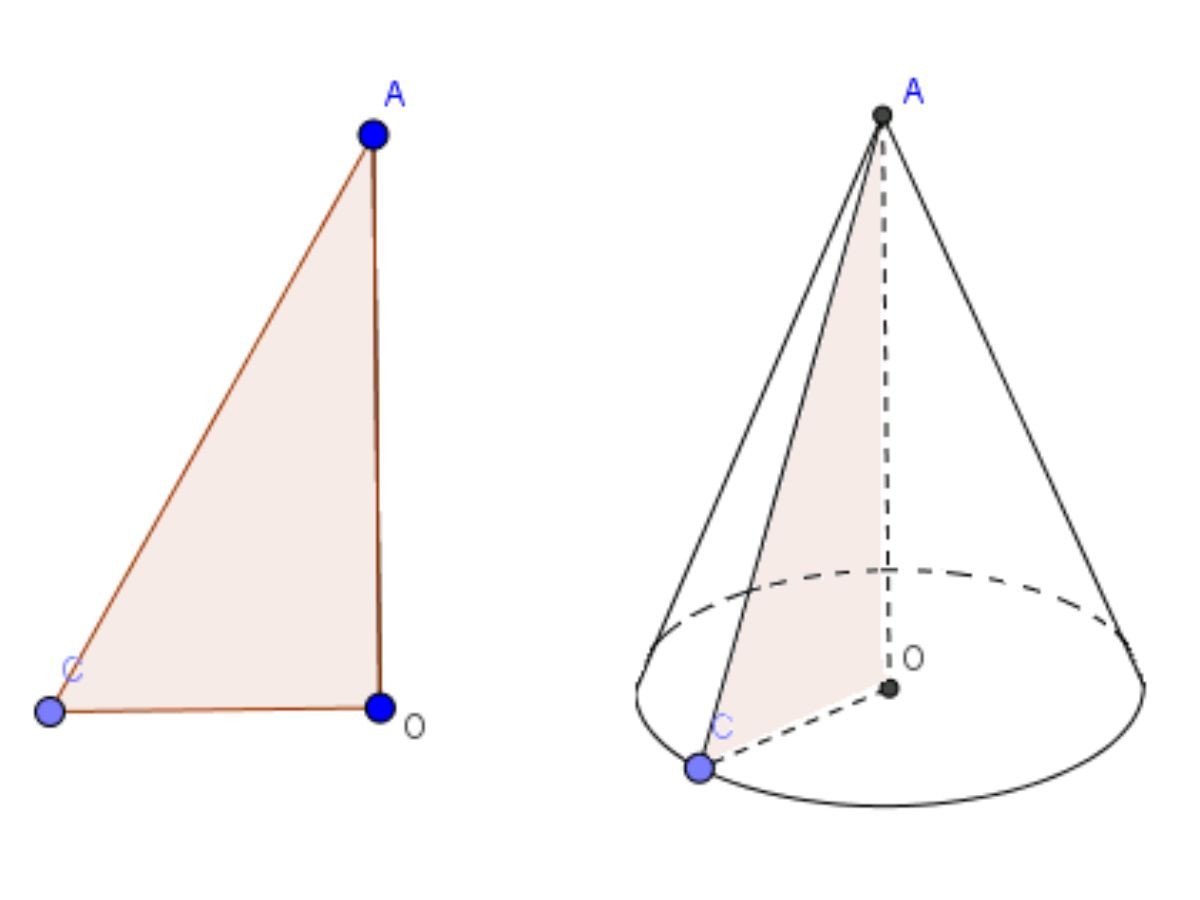
Cách 1: Hình nón được tạo ra khi quay một tam giác vuông một vòng quanh cạnh góc vuông cố định.
Cách 2: Hình nón là hình học không gian 3 chiều đặc biệt, bao gồm một bề mặt phẳng (đáy) và một bề mặt cong hướng lên trên (mặt nón). Đỉnh của hình nón là điểm nhọn nhất, nằm trên trục vuông góc với đáy.
Đặc điểm:
- Hình nón có một đỉnh là hình tam giác, đáy là hình tròn.
- Hình nón không có cạnh.
- Chiều cao của hình nón là khoảng cách từ đỉnh đến tâm đáy.
- Đường sinh của hình nón là đoạn thẳng nối đỉnh với một điểm bất kỳ trên đường tròn đáy.
- Hình nón có thể được chia thành hai phần: phần chóp (phần nhọn) và phần thân (phần từ đáy lên đến chóp).
Ví dụ về hình nón trong đời sống: Nón lá, mũ sinh nhật, phễu, lều trại, chụp đèn...
Hình nón được mô tả trong toán học bằng các yếu tố: đường sinh, đường cao và mặt đáy, giúp việc đo lường và tính toán diện tích toàn phần hình chóp nón dễ dàng hơn trong thực tế. Dưới đây là cách xác định các đơn vị đo lường và ký hiệu cho từng yếu tố:
- Bán kính đáy (ký hiệu: r) là khoảng cách từ tâm mặt đáy đến một điểm bất kỳ trên đường tròn đáy.
- Đường cao (ký hiệu: h) là khoảng cách từ đỉnh của hình nón đến tâm mặt đáy. Đường sinh (ký hiệu: l) là đoạn thẳng nối đỉnh hình nón với một điểm bất kỳ trên đường tròn đáy.
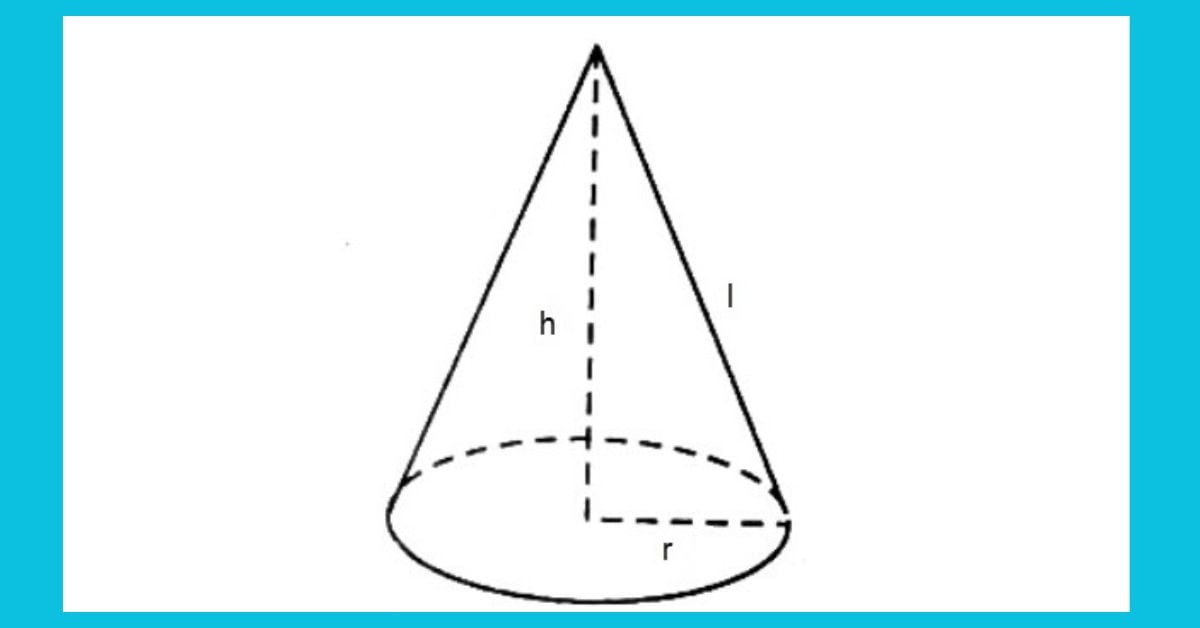
Công thức tính diện tích toàn phần hình chóp nón
Diện tích toàn phần hình chóp nón là tổng cộng diện tích của tất cả các mặt bao quanh hình nón và bao gồm cả mặt xung quanh, mặt đáy.
Công thức tính diện tích toàn phần hình chóp nón:
Stp= Diện tích xung quanh (S_xq) + Diện tích đáy (S_đáy)
Công thức bằng ký hiệu:
S_tp = S_xq + S_đáy = πr² + πrl
Trong đó:
- S_tp: Diện tích toàn phần hình chóp nón (đơn vị: m²)
- S_xq: Diện tích xung quanh của hình nón (đơn vị: m²)
- S_đáy: Diện tích đáy của hình nón (đơn vị: m²)
- r: Bán kính đáy của hình nón (đơn vị: m)
- l: Độ dài đường sinh của hình nón (đơn vị: m)
- π: Hằng số Pi, xấp xỉ bằng 3,14
Ví dụ: Cho một hình nón có bán kính đáy r = 5 cm và đường sinh l = 12 cm. Diện tích toàn phần hình chóp nón này sẽ được tính như sau:
S_tp = πr² + πrl = π5² + π *5*12 ≈ 157 cm²
Những công thức liên quan của hình nón
Ngoài hình chóp nón với đáy là hình tròn, chúng ta còn có hình chóp tam giác và hình chóp tứ giác. Công thức để tính diện tích của những hình này cũng tương đối đơn giản.
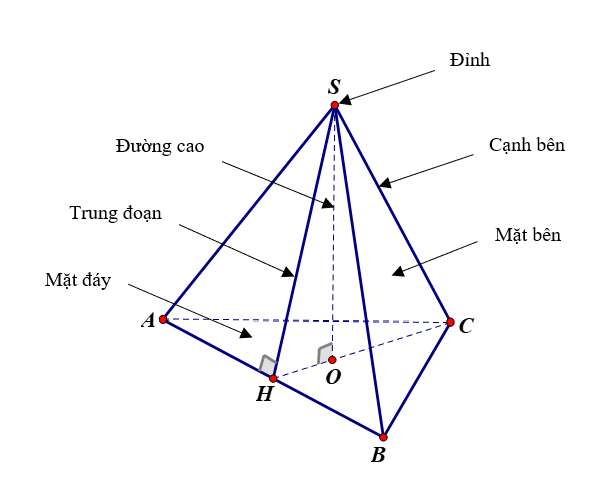
Diện tích toàn phần hình chóp tam giác đều
Diện tích xung quanh của hình chóp tam giác đều là tổng diện tích của tất cả các mặt bên của hình chóp.
Diện tích toàn phần của hình chóp có công thức là tổng diện tích xung quanh và diện tích đáy: Stp =Sxq +S đáy
Trong đó:
- Stp là diện tích toàn phần
- Sxq là diện tích các mặt xung quanh
- S đáy là diện tích mặt đáy
Diện tích toàn phần hình chóp tứ giác đều
Về bản chất, diện tích toàn phần hình chóp tam giác đều và hình chóp tứ giác đều có công thức tương tự nhau: Stp =Sxq +S đáy
Ví dụ: Cho hình chóp tứ giác đều có đáy là hình vuông cạnh 4cm và chiều cao của mỗi mặt bên tam giác là 5cm. Tính diện tích xung quanh và tính diện tích toàn phần hình chóp trên.
Lời giải:
Hình chóp tứ giác đều có 4 mặt bên là tam giác. Do đó, diện tích xung quanh của hình chóp là tổng diện tích của các mặt bên:
Sxq =4 * ½ *4 *5= 40cm2
Diện tích đáy là hình vuông cạnh 4cm:
S đáy= 4* 4 =16 (cm²)
Diện tích toàn phần của hình chóp này là tổng diện tích xung quanh và diện tích đáy:
Stp= S đáy + Sxq = 40+16=56 (cm²)
Diện tích toàn phần hình nón cụt
Diện tích toàn phần (Stp) của hình nón cụt bằng tổng diện tích xung quanh (Sxq) và diện tích của hai mặt đáy (Sđ1 và Sđ2):
Stp = Sxq + Sđ1 + Sđ2
Trong đó:
- Sđ1 và Sđ2 là diện tích của hai mặt đáy hình nón cụt.
- Sxq là diện tích xung quanh của hình nón cụt.
Công thức tính diện tích xung quanh (Sxq) của hình nón cụt:
Sxq = π * (r1 + r2) * l
Trong đó:
- r1 và r2 là bán kính của hai mặt đáy hình nón cụt.
- l là đường sinh của hình nón cụt.
Công thức tính diện tích (S) của mặt tròn:
S = π * r^2 (Trong đó: r là bán kính của mặt tròn.)
Ví dụ: Cho hình nón cụt có bán kính hai mặt đáy lần lượt là r1 = 5cm và r2 = 7cm. Đường sinh của hình nón cụt là l = 6cm. Tính diện tích toàn phần hình chóp nón cụt.
Giải:
Tính diện tích xung quanh (Sxq):
Sxq = π * (r1 + r2) * l = π * (5 + 7) * 6 = 72π (cm²)
Tính diện tích (Sđ1) của mặt đáy nhỏ:
Sđ1 = π * r1^2 = π * 5^2 = 25π (cm²)
Tính diện tích (Sđ2) của mặt đáy lớn:
Sđ2 = π * r2^2 = π * 7^2 = 49π (cm²)
Tính diện tích toàn phần (Stp) của hình nón cụt:
Stp = Sxq + Sđ1 + Sđ2 = 72π + 25π + 49π = 146π (cm²)
Kết luận: Diện tích toàn phần của hình nón cụt là 146π (cm²).
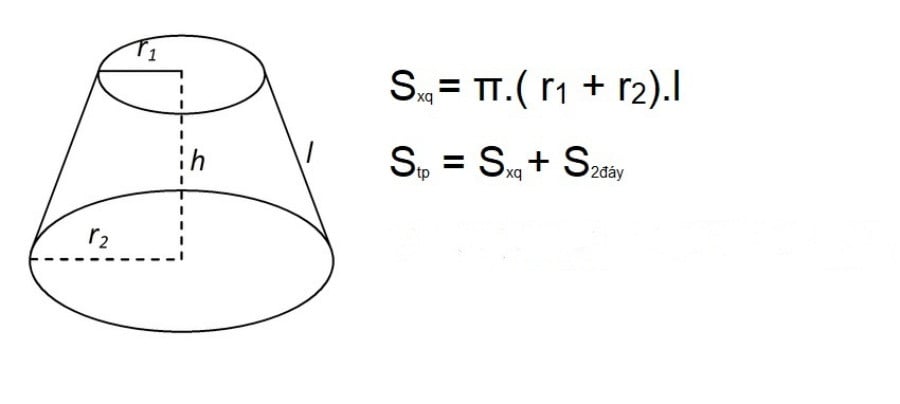
Bài tập thực hành
Bài 1: Cho hình chóp nón đều có đường sinh l = 5cm và bán kính đáy r = 3cm. Tính diện tích toàn phần hình chóp nón cộng với ứng dụng máy tính casio online.
Gợi ý giải:
- Diện tích xung quanh: Sxq = π * r * l = π * 3 * 5 = 15π (cm²)
- Diện tích đáy: Sđ = π * r² = π * 3² = 9π (cm²)
- Diện tích toàn phần: Stp = Sxq + Sđ = 15π + 9π = 24π (cm²)
Bài 2: Cho hình chóp nón cụt có bán kính hai mặt đáy lần lượt là r1 = 4cm và r2 = 6cm. Đường sinh của hình nón cụt là l = 8cm. Tính diện tích toàn phần của hình nón cụt.
Gợi ý giải:
- Diện tích xung quanh: Sxq = π * (r1 + r2) * l = π * (4 + 6) * 8 = 80π (cm²)
- Diện tích mặt đáy lớn: Sđ1 = π * r1² = π * 4² = 16π (cm²)
- Diện tích mặt đáy nhỏ: Sđ2 = π * r2² = π * 6² = 36π (cm²)
- Diện tích toàn phần: Stp = Sxq + Sđ1 + Sđ2 = 80π + 16π + 36π = 132π (cm²)
Bài 3: Một chiếc nón sinh nhật có chiều cao h = 20cm và bán kính đáy r = 15cm. Để trang trí nón, cần bao nhiêu giấy màu có diện tích tối thiểu?
Gợi ý giải:
- Đường sinh của nón: l = √(h² + r²) = √(20² + 15²) = 25cm
- Diện tích xung quanh: Sxq = π * r * l = π * 15 * 25 = 375π (cm²)
- Diện tích đáy: Sđ = π * r² = π * 15² = 225π (cm²)
- Diện tích toàn phần: Stp = Sxq + Sđ = 375π + 225π = 600π (cm²)
Bài 4: Cho hình chóp tứ giác đều có đáy là hình vuông cạnh a = 12cm và độ dài mỗi cạnh mặt bên tam giác đều là b = 10cm. Tính diện tích toàn phần hình chóp nón tứ giác đều.
Gợi ý giải:
Chiều cao của mặt bên tam giác là h =√(10^2- (12/2)^2)) = 8cm
Diện tích xung quanh: Sxq = 4 *½ *8 *12 = 152 (cm²)
Diện tích đáy: Sđ = a² = 12² = 144 (cm²)
Diện tích toàn phần: Stp = Sxq + Sđ = 152 + 144 = 296(cm²)
Bài 5: Một chiếc kem ốc quế có hình dạng như một hình nón cụt. Chiều cao của ốc quế là h = 5cm, bán kính đáy lớn là r1 = 2cm và bán kính đáy nhỏ là r2 = 1cm. Tính diện tích toàn phần của ốc quế (không tính phần diện tích bên trong).
Gợi ý giải:
Đường sinh của ốc quế: l = √(h² + (r1 - r2)²) = √(5² + (2 - 1)²) = √(26) = 5√2.6 (cm)
Diện tích xung quanh: Sxq = π * ((r1 + r2)/2) * l = π * ((2 + 1)/2) * 5√2.6 = 7.85π√2.6 (cm²)
Diện tích mặt đáy lớn: Sđ1 = π * r1² = π * 2² = 4π (cm²)
Diện tích mặt đáy nhỏ: Sđ2 = π * r2² = π * 1² = 1π (cm²)
Diện tích toàn phần: Stp = Sxq + Sđ1 + Sđ2 = 7.85π√2.6 + 4π + 1π = 12.85π√2.6 (cm²)
Một số bài toán nâng cao trong đề thi
Bài 1: Một chiếc đèn lồng hình nón có chiều cao h = 50cm và bán kính đáy r = 30cm. Để trang trí đèn lồng, cần bao nhiêu mét vuông giấy màu? (Không tính mép giấy thừa).
Đường sinh của nón: l = √(h² + r²) = √(50² + 30²) = 60 cm
Diện tích xung quanh: Sxq = π * r * l = π * 30 * 60 = 1800π (cm²)
Diện tích đáy: Sđ = π * r² = π * 30² = 900π (cm²)
Diện tích toàn phần: Stp = Sxq + Sđ = 1800π + 900π = 2700π (cm²)
Diện tích cần thiết để trang trí đèn lồng: S = 2700π (cm²) ≈ 8498.25 cm² ≈ 8.5 m
Bài 2: Một chiếc mũ sinh nhật có hình dạng như một hình nón cụt. Chiều cao của mũ là h = 15cm, bán kính đáy lớn là r1 = 20cm và bán kính đáy nhỏ là r2 = 10cm. Mũ được trang trí bằng một dải ruy băng quấn quanh thân mũ và cả đỉnh mũ theo phương ngang. Tính diện tích ruy băng cần thiết để quấn quanh mũ.
Đường sinh bên của nón cụt: l = √((r1 - r2)² + h²) = √((20 - 10)² + 15²) = 25 cm
Diện tích xung quanh: Sxq = π * ((r1 + r2)/2) * l = π * ((20 + 10)/2) * 25 = 375π (cm²)
Diện tích mặt đáy nhỏ: Sđ2 = π * r2² = π * 10² = 100π (cm²)
Diện tích toàn phần chính là diện tích ruy băng cần là Sxq + Sđ1 = 375π + 400π = 775π (cm²)

Bài tự luyện:
Bài 3: Một kim tự tháp hình chóp tứ giác đều có độ dài cạnh đáy là a = 5m và chiều cao của mỗi mặt bên tam giác đều là h = 8m. Người ta quét vôi toàn bộ mặt ngoài của kim tự tháp (bao gồm cả đáy). Biết diện tích mỗi mét vuông vôi cần 0.5kg vôi để phủ. Tính số lượng kilogam vôi cần thiết để quét vôi cho kim tự tháp.
Bài 4: Cho hình nón cụt (N) có bán kính hai mặt đáy lần lượt là r1 = 4cm và r2 = 6cm. Đường sinh của hình nón cụt là l = 8cm. Gọi O là tâm của mặt đáy lớn và H là chân đường cao hạ từ O xuống mặt đáy nhỏ. Tính diện tích tam giác OMH.
Bài 5: Cho hình chóp tứ giác đều có đáy là hình vuông cạnh a và chiều cao của mỗi mặt bên tam giác đều là h. Gọi O là tâm của đáy, I là trung điểm của một cạnh đáy và M là trung điểm của một cạnh bên. Chứng minh rằng tam giác OIM vuông cân và tính diện tích toàn phần hình chóp nón.
Nhìn chung, các bài toán liên quan đến diện tích toàn phần hình chóp nón là một chủ đề quan trọng và bổ ích trong chương trình toán học. Việc giải các bài toán này giúp học sinh nâng cao kiến thức, kỹ năng toán học, đồng thời phát triển tư duy logic và khả năng giải quyết vấn đề.



























