Hình nón là gì?
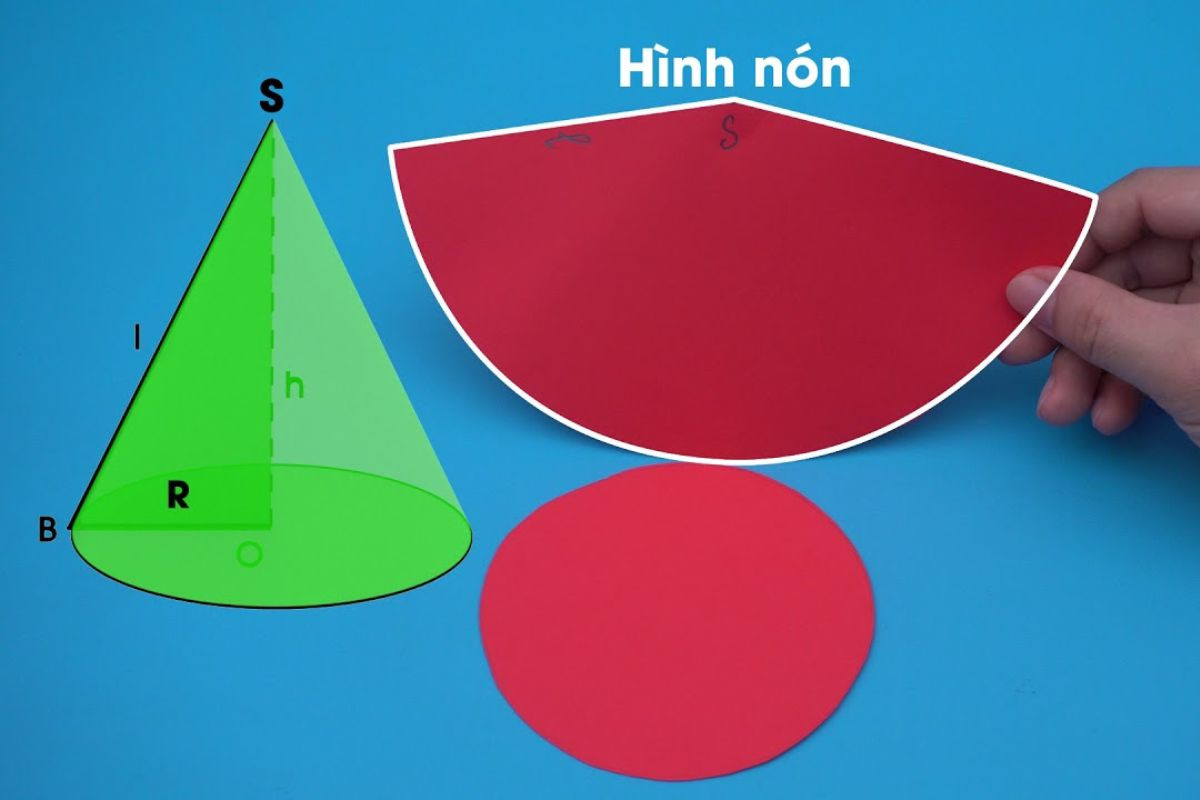
Hình nón là khối hình học không gian 3 chiều, có bề mặt cong hướng lên trên và một bề mặt phẳng. Hình nón được phân chia thành 2 phần gồm đỉnh (phần đầu nhọn) và phần đáy (phần hình tròn mặt phẳng phía dưới). Chiều cao (h) là khoảng cách từ tâm tròn đến đỉnh hình nón.
Bạn có thể bắt gặp nhiều ứng dụng của hình nón trong cuộc sống như mũ sinh nhật, kem ốc quế,... Trong đó hình nón gồm 3 thuộc tính:
- Đỉnh hình tam giác.
- Mặt đáy tròn.
- Không có bất kỳ cạnh nào.

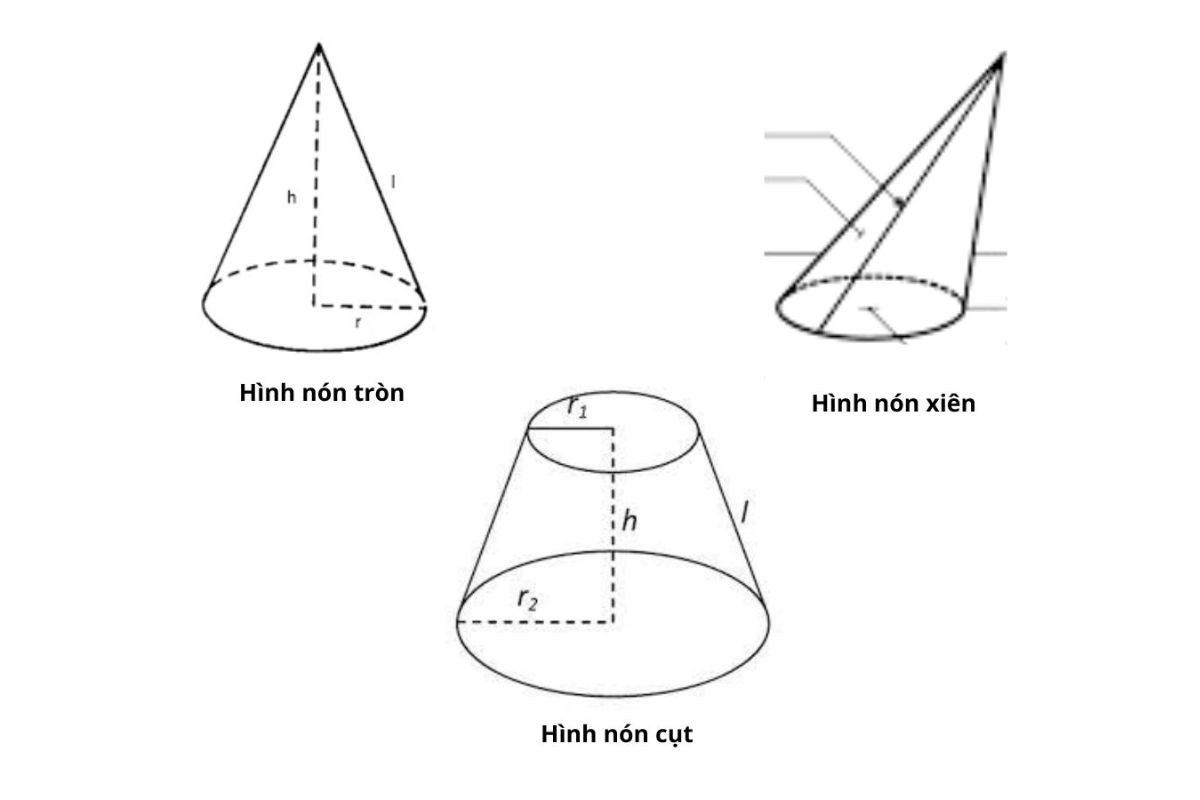
Các loại hình nón phổ biến
Các loại hình nón được phân chia dựa trên vị trí của đỉnh nằm nghiêng hay nằm thẳng, trong đó phổ biến gồm 3 loại:
- Hình nón tròn xoay: Hình nón tròn xoay có đỉnh nối vuông góc với mặt đáy tâm hình tròn.
- Hình nón cụt: Đây là hình nón có hai đáy là hai hình tròn song song với nhau.
- Hình nón xiên: Hình nón xiên có đường cao từ đỉnh không trùng với tâm hình tròn.
Một số công thức tính thể tích hình nón
Mỗi loại hình nón lại có một công thức tính thể tích khác nhau. Cụ thể:
Công thức tính thể tích hình nón tròn xoay
Thể tích hình nón tròn xoay được tính theo công thức như sau:
V = 1/3.S.h = 1/3.π.r2.h.
Trong đó:
- S: Diện tích đáy.
- r: Bán kính đáy.
- h: Chiều cao hình nón.
Công thức tính thể tích hình nón cụt
Thể tích hình nón cụt được tính bằng hiệu của thể tích hình nón lớn và hình nón nhỏ. Cụ thể:
V = 1/3π(r12+r22+ r1r2) . Trong đó:
- r1, r2: Bán kính hai đáy.
- h: Chiều cao.
Một số công thức khác về hình nón
Sau khi nắm được công thức tính thể tích hình nón, bạn cũng nên tham khảo các công thức tính khác liên quan đến hình tròn dưới đây để áp dụng linh hoạt vào bài tập.
Công thức tính diện tích xung quanh hình nón
Diện tích hình tròn được tính theo công thức sau:
Sxq = π.r.l
Trong đó:
- r: Bán kính đáy.
- l: Độ dài đường sinh.
Công thức tính diện tích toàn phần hình nón
Diện tích hình nón được hiểu là toàn bộ phần không gian nằm phía trong của hình nón, bao gồm phần diện tích xung quanh và diện tích toàn phần của hình nón. Công thức tính diện tích toàn phần hình nón được tính như sau:
Stp = Sxq + S(đáy) = π.r.l + π.r2
Trong đó:
- S (đáy): Diện tích hình nón.
- r: Bán kính đáy hình tròn.
- l: Độ dài đường sinh.
Công thức tính diện tích mặt đáy hình nón
Diện tích đáy hình nón được tính theo công thức Sđáy= π.r2, trong đó r là bán kính hình tròn.
Cách xác định đường sinh, đường cao và bán kính đáy
Hình nón được tạo thành khi quay một hình tam giác quanh trục một cạnh góc vuông. Theo đó, bán kính đáy và đường cao sẽ là 2 cạnh góc vuông của tam giác, đường sinh là cạnh huyền. Các công thức bao gồm:
- l = r2+h2: Công thức tính đường sinh khi nắm được đường cao h và bán kính đáy.
- h = l2 - r2: Công thức tính đường cao khi biết bán kính và đường sinh.
- r = l2- h2 : Công thức tính bán kính đáy khi biết chiều cao và đường sinh.
Một số phần mềm và công cụ trực tuyến giúp tính thể tích hình nón
Ngoài sử dụng công thức tính thể tích hình nón, bạn có thể sử dụng các phần mềm và công cụ trực tuyến. Một số công cụ bạn có thể tham khảo bao gồm:
- GeoGebra: Đây là công cụ học tập đa năng và nổi bật với khả năng giải toán và thực hiện các phép tính hình học, trong đó bao gồm các bài toán tính thể tích hình tròn.
- Wolfram Alpha: Wolfram Alpha là một công cụ tính toán mạnh mẽ với nhiều bài toán phổ thông khác nhau, ở nhiều cấp độ khó nhất định.
- Symbolab: Trang web giáo dục Symbolab cung cấp các công cụ giải toán, tích hợp tính năng nhập công thức và tính kết quả của nhiều dạng khác nhau.
- Calculator Soup: Đây là nền tảng trực tuyến với các công cụ tính toán tối ưu, phục vụ cho nhiều mục đích khác nhau.

Lưu ý khi tính thể tích hình nón
Trong quá trình thực hiện tính thể tích hình nón, một số lưu ý quan trọng bạn cần ghi nhớ để thu được kết quả chính xác như:
- Kiểm tra đơn vị: Bạn cần chắc chắn rằng tất cả đơn vị đều được chuyển đổi sang cùng một hệ đo lường.
- Tính toán, nhập liệu chính xác: Khi nhập số liệu vào máy tính hoặc công cụ trực tuyến, bạn cần đảm bảo đầu vào được nhập một cách chính xác, tránh nhầm lẫn giữa các thông số liên quan.
- Đánh giá kết quả: Sau khi tính toán, bạn cần xem xét kết quả cuối cùng có phù hợp với kích thước và hình dạng của hình nón không.
Tổng hợp các công thức về hình nón cần phải nhớ
Các công thức bạn cần lưu tâm khi áp dụng vào các bài toán liên quan đến thể tích hình tròn bao gồm:
|
STT |
Nội dung |
Công thức |
|
1 |
Thể tích |
V = 1/3.S.h = 1/3.π.r2.h |
|
2 |
Diện tích |
S = S (đáy) + Sxq = π.r.(r+l) |
|
3 |
Diện tích đáy |
S (đáy) = π.r2 |
|
4 |
Diện tích xung quanh |
Sxq = π.r.l |
|
5 |
Đường sinh |
l = h2+ r2 |
|
6 |
Chu vi |
P = π.r.l |
|
7 |
Đường kính |
d= 2.r |
Một số bài tập tính thể tích hình nón
Sau khi nắm được công thức tính thể tích hình nón, bạn có thể thực hành một số dạng bài tập liên quan để áp dụng các công thức trên một cách thành thạo công với công cụ tính toán là máy tính casio online. Một số dạng toán phổ biến bao gồm:
- Bài 1: Cho hình nón có bán kính đáy là 4a, chiều cao là 3a. Tính đường sinh, diện tích xung quanh, diện tích toàn phần và thể tích của hình nón trên.
- Bài 2: Cho hình nón có đường sinh l, góc giữa đường sinh và mặt phẳng đáy là 30º. Tính diện tích xung quanh của hình nón.
- Bài 3: Một khối nón có thể tích bằng 30 π, nếu giữ nguyên chiều cao và tăng bán kính khối nón đó lên 2 lần thì thể tích của khối nón mới bằng bao nhiêu?
- Bài 4: Cắt một hình nón bằng một mặt phẳng qua trục của nó ta được thiết diện là một tam giác đều cạnh 2a. Tính diện tích xung quanh của hình nón.
- Bài 5: Cắt hình nón đỉnh S bởi mặt phẳng đi qua trục ta được một tam giác vuông cân có cạnh huyền bằng a√2. Tính thể tích khối nón.
- Bài 6: Một hình nón có đường sinh bằng 3cm và góc ở đỉnh bằng 90°. Cắt hình nón bởi mặt phẳng (α) đi qua đỉnh sao cho góc giữa (α) và mặt đáy bằng 60°. Tính diện tích thiết diện.
Thể tích hình nón không chỉ là khái niệm trừu tượng trong sách giáo khoa mà còn được ứng dụng nhiều trong đời sống và kỹ thuật như kiến trúc, xây dựng, công nghiệp, thiết kế đồ hoạ,.... Để nâng cao kỹ năng tính thể tích thành thạo và chính xác, bạn cần thực hành với nhiều dạng toán khác nhau.



























