Khái niệm, tính chất của hình thoi
Hình thoi là một dạng đa giác đặc biệt trong hình học phẳng, được xác định bởi bốn cạnh bằng nhau và bốn góc. Trước khi đi sâu hơn vào tìm hiểu cách tính diện tích hình thoi, chúng ta cần hiểu rõ về định nghĩa cũng như các đặc điểm cơ bản của nó. Điều này giúp chúng ta xây dựng nền tảng vững chắc khi áp dụng các tính chất của hình thoi vào các bài toán và tình huống thực tế.
Hình thoi là gì?
Trong hình học Euclide, hình thoi là một tứ giác có bốn cạnh bằng nhau. Đặc điểm này cũng cho thấy nó là một hình bình hành với hai cạnh kề bằng nhau hoặc hai đường chéo vuông góc.
Khi một hình thoi có bốn góc vuông, nó trở thành hình vuông. Do đó, hình vuông là một trường hợp đặc biệt của hình thoi vì nó không chỉ có bốn cạnh bằng nhau mà còn có bốn góc vuông.
Từ đây, ta có thể rút ra các kết luận sau:
- Tất cả các hình vuông đều là hình thoi nhưng không phải tất cả các hình thoi đều là hình vuông.
- Tất cả các hình thoi đều có thể coi là hình bình hành nhưng không phải hình bình hành nào cũng đều là hình thoi.
Tính chất của hình thoi
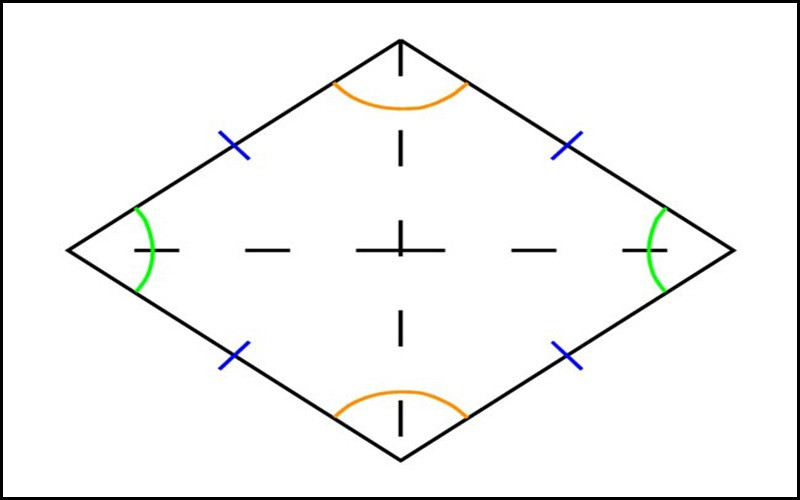
Hình thoi có các tính chất sau:
- Các góc đối diện của hình thoi bằng nhau.
- Hai đường chéo sẽ cắt nhau và vuông góc tại trung điểm của mỗi đường.
- Hai đường chéo cũng là các đường phân giác của các góc.
- Hình thoi sở hữu các tính chất của hình bình hành.
Dấu hiệu nhận biết hình thoi
Để xác định một hình có phải là hình thoi hay không, chúng ta có thể dựa vào các dấu hiệu sau:
- Một tứ giác có độ dài 4 cạnh bằng nhau thì chính là hình thoi.
- Tứ giác có hai đường chéo là đường trung trực của nhau được coi là hình thoi.
- Nếu tứ giác có hai đường chéo là đường phân giác của cả bốn góc thì đó là hình thoi.
- Hình bình hành có hai cạnh kề bằng nhau thì được xem là hình thoi.
- Hình bình hành có hai đường chéo vuông góc nhau chính là hình thoi.
- Hình bình hành có một đường chéo là đường phân giác của một góc thì được xem là hình thoi.
Công thức tính diện tích hình thoi
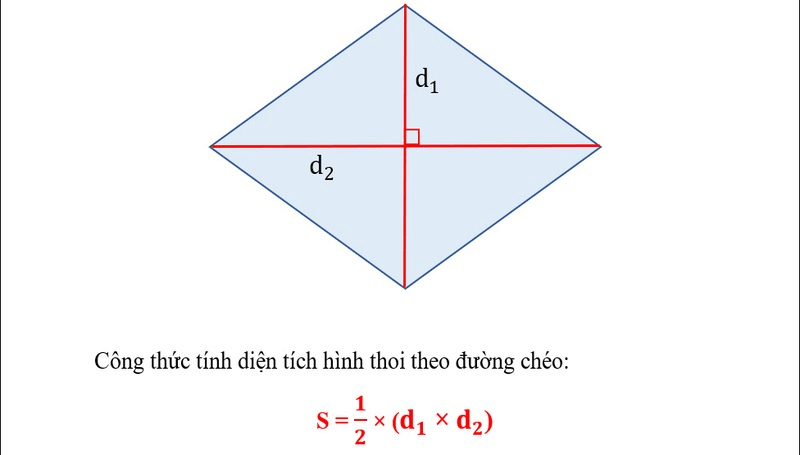
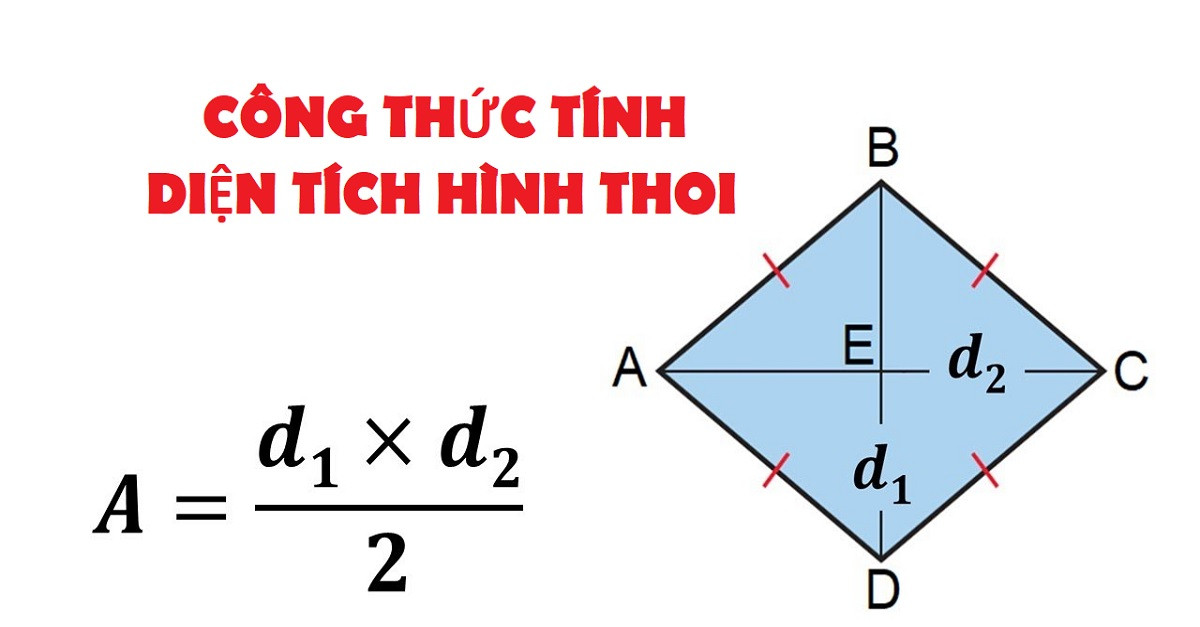
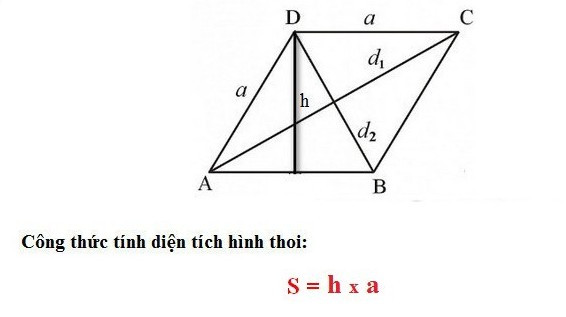
Muốn tính diện tích hình thoi, ta có thể áp dụng công thức được diễn đạt như sau: Diện tích của hình thoi bằng một phần hai tích độ dài của hai đường chéo.
S = 1/2× d1×d2
Hoặc: S = a x h
Trong đó:
- S là diện tích hình thoi
- d1 và d2 là độ dài của hai đường chéo hình thoi
- a là độ dài cạnh hình thoi
- h là chiều cao hình thoi
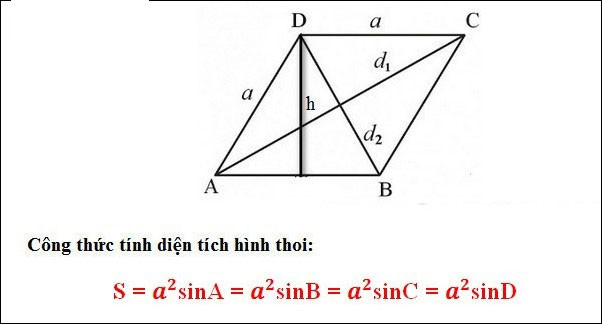
Ngoài ra, diện tích của hình thoi cũng có thể được tính bằng công thức liên quan đến góc của hình thoi (trong trường hợp biết số đo của góc):
S = a² x sin(α)
Trong đó:
- S: Diện tích hình thoi
- a: Độ dài cạnh bên
- α: Số đo số đo của một góc bất kỳ trong hình thoi
Một số dạng toán tính diện tích hình thoi thường gặp
Tính diện tích của hình thoi là một trong những kỹ năng cơ bản mà học sinh cần nắm vững trong học tập hình học. Tuy nhiên, không phải lúc nào việc tính diện tích cũng diễn ra đơn giản. Tuỳ vào các thông tin được cung cấp trong bài toán, học sinh sẽ phải vận dụng các công thức và các tính chất của hình thoi để tìm ra được diện tích chính xác.
Dạng 1: Tính diện tích hình thoi theo đường chéo
Với dạng bài tập này, ta tiến hành theo các bước sau:
- Xác định dữ kiện đề bài cho và tính độ dài của hai đường chéo.
- Nhân độ dài của hai đường chéo với nhau.
- Sau đó chia kết quả vừa tính được cho 2.
Ở dạng bài tập này, việc tính chính xác độ dài của hai đường chéo là điều quan trọng để tính diện tích hình thoi. Do đó, cần tư duy nhanh nhạy và chính xác dựa trên các dữ kiện mà đề bài cung cấp.
Bài tập ví dụ: Một hình thoi có độ dài một cạnh bằng 15cm, một trong hai đường chéo có độ dài bằng 18cm.
Giải: Do 2 đường chéo của hình thoi vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường, do đó chúng tạo thành bốn tam giác vuông.
Áp dụng định lý Pythagore để tính độ dài đường chéo d2:
d2 = 2 x √(15^2 – 9^2) = 2 x 12 = 24
Vậy diện tích của hình thoi S = 1/2 x d1 x d2 = 1/2 x 18 x 24 = 216 cm^2.
Dạng 2: Tính diện tích hình thoi theo độ dài chiều cao và cạnh đáy
Do hình thoi có đầy đủ các tính chất của tứ giác đặc biệt, với hai cạnh kề và đáy bằng nhau, chúng ta có thể sử dụng công thức sau để tính diện tích hình thoi:
S = a x h
Với: S là diện tích của hình thoi; a là độ dài cạnh đáy và h là chiều cao của hình thoi
Để giải bài tập này, ta thực hiện theo các bước sau:
- Xác định thông tin đề bài cho, tính độ dài cạnh đáy và chiều cao của hình thoi.
- Áp dụng công thức tính diện tích bằng cách lấy độ dài chiều cao nhân với cạnh đáy.
Bài tập ví dụ: Tính diện tích hình thoi có chiều cao 7cm và độ dài cạnh đáy là 90mm.
Giải:
Ta thực hiện quy đổi: 90 mm = 9 cm.
Độ dài cạnh đáy của hình thoi là 9 cm.
Áp dụng công thức: S = a x h = 7cm x 9cm = 63cm^2
Vậy diện tích của hình thoi trong bài tập ví dụ 2 là 48cm^2.
Dạng 3: Tính diện tích dựa vào công thức lượng giác
Để tính diện tích hình thoi khi biết độ dài cạnh và góc giữa hai cạnh, chúng ta sử dụng công thức:
S = a^2 × sin(α)
Trong đó:
- a là độ dài cạnh đáy của hình thoi
- α là góc giữa hai cạnh của hình thoi
Bài tập ví dụ: Cho hình thoi MNPQ có cạnh bằng 5 cm và góc A = 40 độ. Tính diện tích hình thoi MNPQ.
Giải:
Ta có: a = 6 cm; Góc A = 40 độ
Thay vào công thức:
S = a^2 × sin(α) = 5^2 × sin(40°) = 25 × 0.6428 = 16.07cm^2
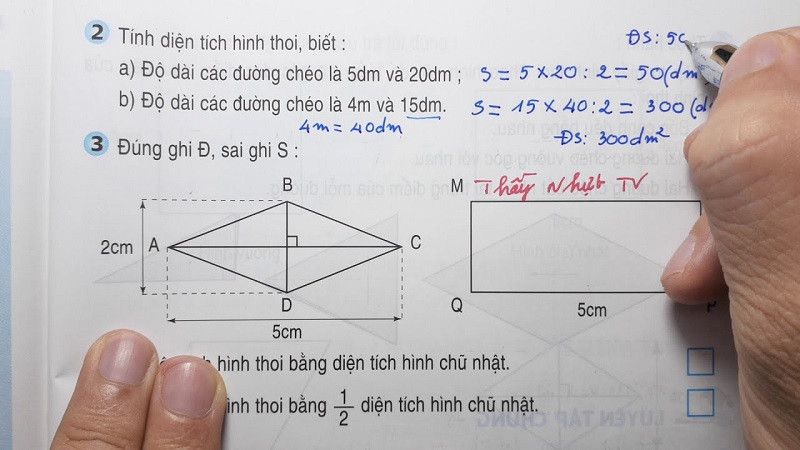
Những lưu ý khi làm bài toán tính diện tích
Trong các bài tập hoặc bài kiểm tra có nhiều bài toán tính diện tích nhằm gây nhiễu cho học sinh, cần chú ý các điểm sau để làm bài hiệu quả:
- Khi đề bài cho độ dài các cạnh với các đơn vị đo khác nhau, bước đầu tiên là quy đổi tất cả về cùng một đơn vị đo.
- Khi so sánh diện tích các hình, cũng cần chú ý đến đơn vị đo diện tích. Nếu các đơn vị khác nhau, hãy quy đổi về cùng một đơn vị đo trước khi tiến hành so sánh.
- Hãy kiểm tra kết quả ít nhất hai lần để đảm bảo tính chính xác.

Các bài toán ứng dụng liên quan đến diện tích hình thoi
Sau khi đã nắm được các cách tính diện tích hình thoi, bạn đọc cần áp dụng và thực hành ngay để củng cố kiến thức cũng như rèn luyện kỹ năng giải nhanh. Dưới đây là các bài tập diện tích hình thoi mẫu:
Bài tập 1
Cho một mảnh đất trống hình thoi với tổng độ dài hai đường chéo bằng 600 cm. Trong đó, chiều dài của đường chéo thứ nhất bằng 2/3 chiều dài của đường chéo thứ hai. Hãy tính diện tích của mảnh đất trống này.
Giải:
Trước hết, ta xác định tổng số phần được chia từ hai đường chéo. Tổng số phần là 2 + 3 = 5 phần.
Chiều dài của đường chéo thứ hai là: 600/5 x 3 = 360
Chiều dài của đường chéo thứ nhất là: 600 - 360 = 240
Diện tích của hình thoi được tính theo công thức: S = ½ x (d1xd2) = ½ x 360 x 240 = 43200 cm^2
Bài tập 2
Cho một khu vườn dạng hình thoi có đường chéo thứ nhất dài 24m và đường chéo thứ hai có độ dài bằng 3/4 chiều dài của đường chéo thứ nhất. Người nông dân trồng khoai tây trên khu vườn, với mỗi mét vuông sẽ thu được khoảng 7kg khoai lang. Hỏi người nông dân này sẽ thu được bao nhiêu kg khoai tây?
Giải:
Tính độ dài của đường chéo thứ hai: ¾ x 24 = 18
Diện tích khu vườn hình thoi:
S = ½ x 24 x 18 = 216 m^2
Vậy số kg khoai tây thu được trong khu đất là:
Số ký khoai = 216 x 7 = 1512 kg
Bài tập 3
Trong hình thoi MNPQ - ABCD , điểm O được coi là giao điểm của hai đường chéo. Diện tích của hình thoi này là 60 cm2, cạnh MP dài 10 cm. Hãy tính chiều dài cạnh của hình thoi này.
Giải:
Áp dụng công thức tính diện tích hình thoi theo máy tính online casio fx-580vn plus:
S = 1/2 × MP × NQ
Suy ra:
NQ = (2 × S)/MP
NQ = (2 × 60)/10 = 12 cm
Vì là hình thoi, nên điểm O là trung điểm của cả MP và NQ.
Như vậy:
OM = 1/2 × MP = 1/2 × 10 = 5 cm
ON = 1/2 × NQ = 1/2 × 12 = 6 cm
Áp dụng định lý Pytago cho tam giác MON:
MN^2 = OM^2 + ON^2 = 5^2 + 6^2 = 61
Suy ra: MN = √61 ≈ 7,81 cm
Vậy chiều dài các cạnh của hình thoi MNPQ là khoảng 7,81 cm.
Diện tích hình thoi không chỉ là một khái niệm toán học trừu tượng mà còn có vô số ứng dụng thiết thực trong cuộc sống hàng ngày. Nắm vững các công thức và kỹ thuật tính diện tích hình thoi không chỉ giúp giải quyết các vấn đề toán học mà còn hỗ trợ chúng ta trong nhiều lĩnh vực ứng dụng khác. Vì vậy, việc nghiên cứu và thành thạo các bài toán liên quan đến diện tích hình thoi là một kỹ năng vô cùng cần thiết.



























