Định nghĩa hình cầu là gì?
Trước khi tìm hiểu công thức tính thể tích hình cầu, bạn cần nắm được các định nghĩa về loại hình học không gian này. Hình cầu được tạo bởi toàn bộ không gian tính từ mặt cầu đến tâm của nó. Thể tích khối cầu được hiểu là tất cả phần không gian của khối cầu hoặc phần không gian ở phía bên trong của mặt cầu.
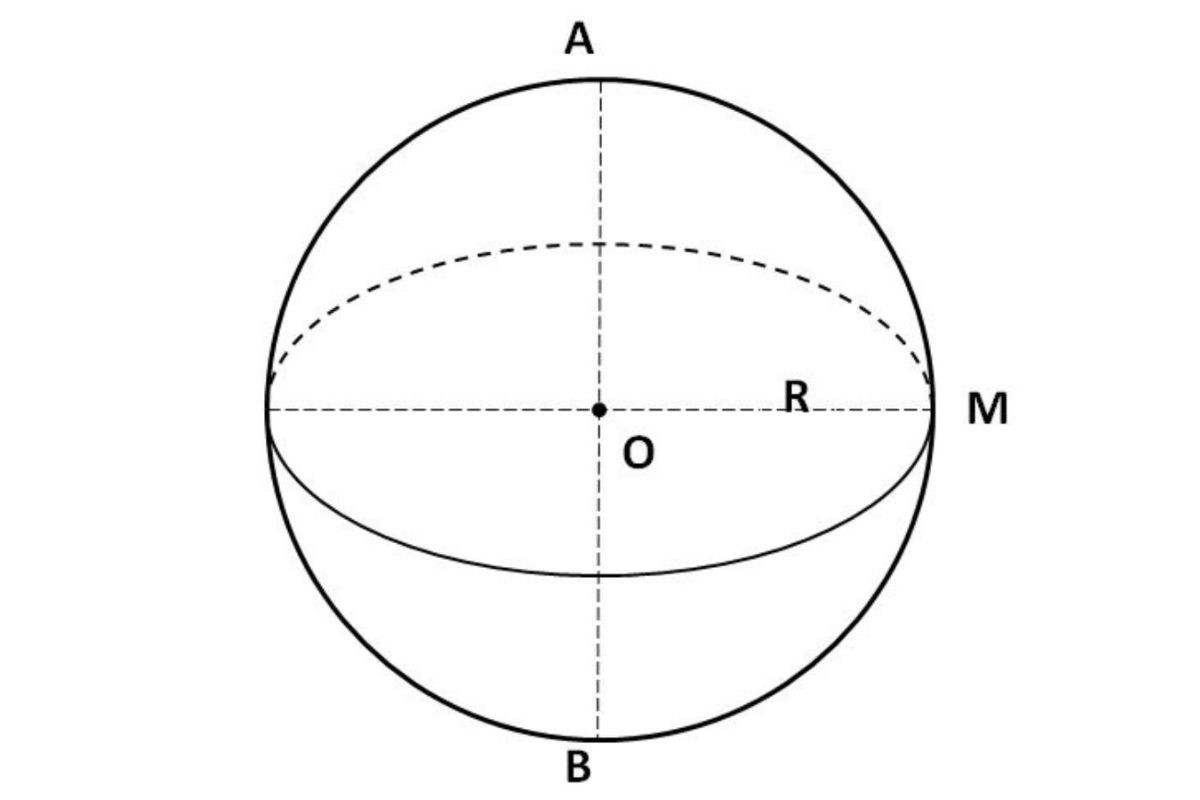
Công thức tính thể tích hình cầu
Bạn có thể tính thể tích hình cầu theo công thức:
V = 4.π.r3/3.
Trong đó:
- V: Thể tích khối cầu.
- Π: số pi, tính theo giá trị 3,14.
- r: Bán kính hình cầu.
Một số công thức khác liên quan đến hình cầu
Để làm tốt các bài tập về hình học không gian, đặc biệt là hình cầu, bạn có thể tham khảo thêm một số công thức dưới đây:
Công thức dùng để tính diện tích của mặt cầu
Công thức tính diện tích mặt cầu hay diện tích xung quanh hình cầu là:
S = 4π.r2.
Trong đó:
- S là diện tích mặt cầu.
- r là bán kính hình cầu.
- π là hằng số toán học, xấp xỉ bằng 3,14.
Thể tích khối cầu nội tiếp hình lập phương
Công thức tính thể tích khối cầu nội tiếp hình lập phương là V = π.a3/6. Trong đó:
- V là thể tích hình cầu.
- a là chiều dài cạnh của hình lập phương.
Thể tích khối cầu ngoại tiếp hình lập phương
Công thức tính thể tích khối cầu ngoại tiếp hình lập phương là V = π.a33/2. Trong đó:
- V là thể tích hình cầu.
- a là chiều dài cạnh của hình lập phương.
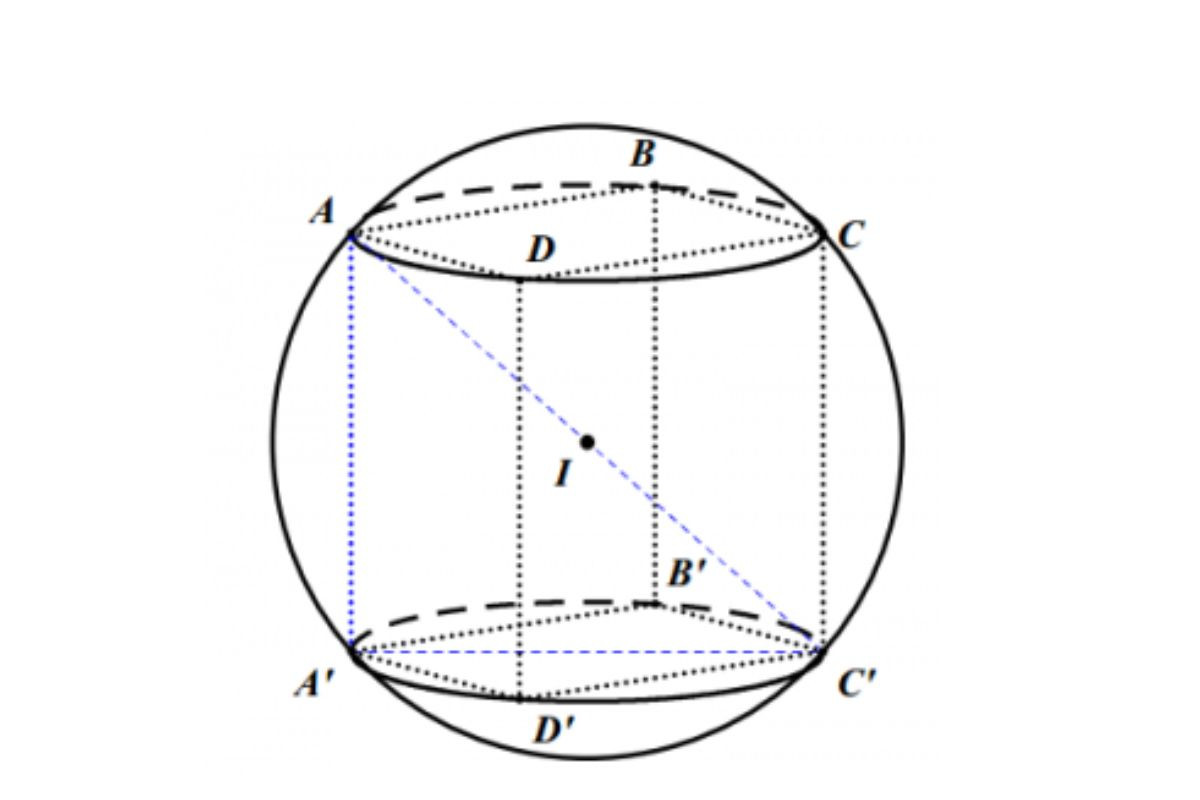
Thể tích khối cầu ngoại tiếp hình chóp
Thể tích khối cầu ngoại tiếp hình chóp được tính theo công thức V = 4.π.r3/3. Trong đó, bán kính r có thể được tính dựa trên đặc điểm cụ thể của từng hình chóp.
Cách tìm bán kính của khối cầu khi biết thể tích
Công thức chung để tính bán kính của khối cầu khi biết thể tích là r3 = 3V/4π. Trong đó:
- V là thể tích hình cầu.
- r là bán kính hình cầu.
Hướng dẫn chi tiết các bước tính thể tích khối cầu
Để thực hiện các bài toán tính thể tích hình cầu, bạn có thể áp dụng các bước sau:
- Bước 1: Viết công thức cần sử dụng ra giấy.
- Bước 2: Đọc kỹ đề bài và chọn lọc các thông tin.
- Bước 3: Tính luỹ thừa của bán kính.
- Bước 4: Thay thế các giá trị đã có vào công thức để tính thể tích hình cầu.
Vì sao diện tích của mặt cầu bằng 4 lần diện tích của hình tròn lớn?
Lý giải vì sao diện tích mặt cầu bằng 4 lần diện tích hình tròn lớn, bạn cần dựa trên các công thức để đưa ra suy luận tương ứng. Cụ thể:
- Diện tích mặt cầu được tính theo công thức: S = 4πr2, trong đó r là bán kính của mặt cầu.
- Diện tích hình tròn được tính theo công thức S = πr2, r là bán kính hình tròn.
So sánh công thức trên, bạn có thể thấy diện tích của mặt cầu bằng 4 lần diện tích của hình tròn trên cùng bán kính r.
Vì sao diện tích của mặt cầu bằng 4 lần hằng số π nhân bình phương bán kính r?
Xét trên phương diện hình học, diện tích bề mặt hình cầu là tổng diện tích các vòng tròn bán kính thay đổi từ 0 đến bán kính r. Khi đó, ta có thể thấy, mỗi vòng tròn có bán kính phụ thuộc vào vị trí của chúng trên mặt cầu khi di chuyển lần lượt từ 0 đến chiều dài bán kính r.
Mối quan hệ giữa bán kính r và thể tích hình cầu
Thể tích hình cầu có thể hiểu là lượng vật chất mà khối cầu chiếm giữ. Trong đó, bán kính hình cầu là khoảng cách từ tâm đến một điểm trên bề mặt khối cầu. Công thức tính thể tích hình cầu là V = 4.π.r3/3, trong đó V là thể tích hình cầu, r là bán kính khối cầu và π là chỉ số bất định. Từ đây, ta có thể suy luận nếu bán kính hình cầu tăng gấp đôi thì thể tích khối cầu sẽ tăng gấp 8 lần.
Ứng dụng công thức để xác định thể tích hình cầu trong thực tế
Bằng cách tính thể tích hình cầu trên, con người đã áp dụng công thức này vào nhiều lĩnh vực thực tế như:
- Toán học: Công thức này được sử dụng trong các bài toán về hình học không gian, thể tích của các vật có hình cầu như quả bóng, trái đất.
- Kiến trúc: Kiến trúc sư có thể áp dụng việc tính thể tích vào thiết kế và xây dựng các công trình có hình cầu như hồ nước, bể nước, bể chứa, vòi phun nước,...
- Công nghệ xây dựng: Bên xây dựng sẽ tính toán lượng vật liệu cho các công trình dạng hình cầu như hầm chui, đường ống ngầm,...
- Vật lý: Công thức tính thể tích được sử dụng trong tính toán khối lượng của các vật thể có hình cầu như chất khí, chất lỏng,..
- Cơ học: Nhà khoa học có thể tính toán lực tác động cơ học lên các vật thể có hình cầu như quả bóng bay nảy lên khỏi mặt đất,...

Một số bài tập tính thể tích hình cầu thường gặp
Các dạng bài tập về thể tích hình cầu học sinh có thể tham khảo để ôn tập và ứng dụng thành thạo trong dạng đề hình học không gian:
- Bài 1: Một hình cầu có bán kính r = 4 cm. Tính thể tích của hình cầu này.
- Bài 2: Cho mặt cầu có số đo thể tích bằng số đo diện tích. Tìm bán kính mặt cầu đó.
- Bài 3: Một hình cầu có R = 3cm và một hình nón cũng có r đáy = 3cm, diện tích toàn phần bằng diện tích mặt cầu. Tìm chiều cao của hình nón đó.
- Bài 4: Một hình cầu có S mặt cầu = 64π (cm2). Tìm thể tích khối cầu đó?
- Bài 5: Một hình trụ có r đường tròn đáy = 3cm và h = 4cm. Một hình cầu có diện tích bằng diện tích xung quanh của hình trụ. Tìm bán kính của hình cầu đó?
- Bài 6: Một hình cầu nội tiếp bên trong hình trụ. Biết rằng chiều cao của hình trụ bằng ba lần bán kính đáy và bán kính đáy hình trụ bằng bán kính của hình cầu. Tìm tỉ số giữa thể tích hình cầu và thể tích hình trụ?
- Bài 7: Cho một hình lập phương ngoại tiếp với một hình cầu. Nếu diện tích toàn phần hình lập phương bằng 24cm2 thì diện tích mặt cầu là bao nhiêu?
- Bài 8: Cho tam giác ABC vuông cân tại A với cạnh góc vuông là a. Tính diện tích mặt cầu được tạo thành khi ta quay nửa đường tròn ngoại tiếp tam giác ABC một vòng xung quanh cạnh BC.
Thể tích hình cầu là một công thức quan trọng trong toán học. Ngoài ra, công thức này được ứng dụng trên nhiều lĩnh vực như định lượng không gian, xử lý số liệu trong xây dựng và thiết kế đa ngành nghề, đặc biệt là kiến trúc kết hợp với máy tính online casio fx-580vn plus.



























