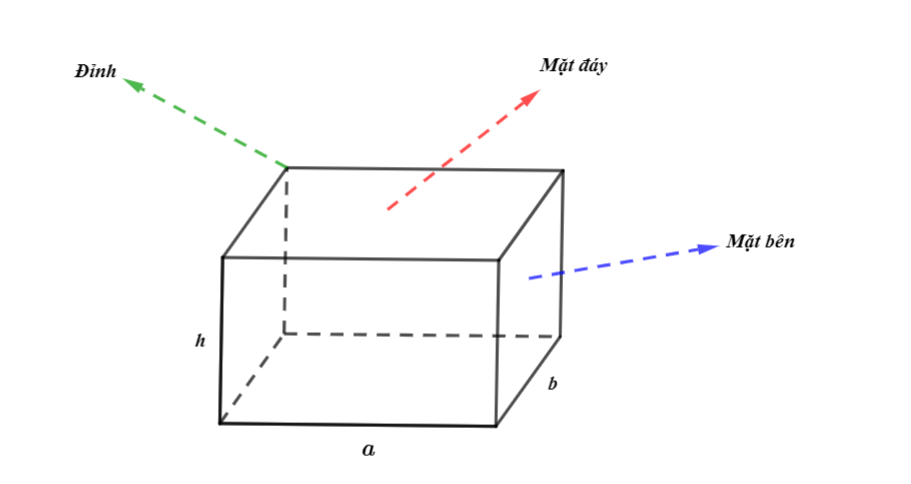
Hình hộp chữ nhật là gì?
Hình hộp chữ nhật là một hình không gian với 6 mặt đều là hình chữ nhật. Hai mặt của hình hộp chữ nhật không chứa cạnh chung được gọi là mặt đối diện và có thể xem chúng là hai mặt đáy, các mặt còn lại sẽ được xem là các mặt bên.
Đặc điểm của hình hộp chữ nhật:
- Có 8 đỉnh, có 12 cạnh và 6 mặt.
- Các cạnh đối diện của hình hộp chữ nhật có độ dài bằng nhau và song song với nhau.
- Các mặt của hình hộp chữ nhật là các hình chữ nhật vuông góc với nhau.
- Hình hộp chữ nhật có 4 đường chéo, mỗi đường chéo nối giữa 2 đỉnh không kề nhau của hình hộp chữ nhật.
Hình hộp chữ nhật được ứng dụng rộng rãi trong đời sống, ví dụ như: Gạch, đá xây dựng, hộp đựng thực phẩm, bàn ghế, tủ, container,... thường có hình dạng hình hộp chữ nhật.

Công thức tính thể tích hình hộp chữ nhật
Thể tích của một vật thể là số đo lượng không gian mà vật thể đó chiếm giữ. Thể tích của hình hộp chữ nhật được tính bằng tích của chiều dài, chiều rộng và chiều cao của nó.
Công thức thể tích hình hộp chữ nhật: V = a x b x h
Giải thích:
- V: Thể tích của hình hộp chữ nhật (đơn vị: mét khối, cm khối,...)
- a: Chiều dài của hình hộp chữ nhật (đơn vị: mét, cm,...)
- b: Chiều rộng của hình hộp chữ nhật (đơn vị: mét, cm,...)
- h: Chiều cao của hình hộp chữ nhật (đơn vị: mét, cm,...)
Ví dụ: Giả sử ta có một hình hộp chữ nhật có chiều dài 5 cm, chiều rộng 4 cm và chiều cao 3 cm. Thể tích hình hộp chữ nhật này được tính như sau:
V = 5 cm x 4 cm x 3 cm = 60 cm3
Bài tập tính thể tích của hình hộp chữ nhật
Để thành thạo các bài toán từ cơ bản đến nâng cao liên quan đến tính toán thể tích hình hộp chữ nhật, hãy theo dõi những dạng bài kèm ví dụ minh họa sau:
Tính thể tích của một hộp chữ nhật biết độ dài các cạnh
Bước 1: Phân tích đề bài để xác định các giá trị đã biết: chiều dài (a), chiều rộng (b) và chiều cao (h) của hình hộp chữ nhật.
Bước 2: Áp dụng công thức tính thể tích: V = a x b x h.
Bước 3: Thay số và tính toán kết quả.
Bước 4: Kiểm tra lại kết quả và ghi chú đáp số.
Ví dụ 1: Tính thể tích của một hộp chữ nhật có chiều dài 5 cm, chiều rộng 4 cm và chiều cao 3 cm áp dụng công cụ máy tính online casio fx-580vn.
Giải:
Thể tích của hình hộp chữ nhật là: V = a x b x h = 5 cm x 4 cm x 3 cm = 60 cm3
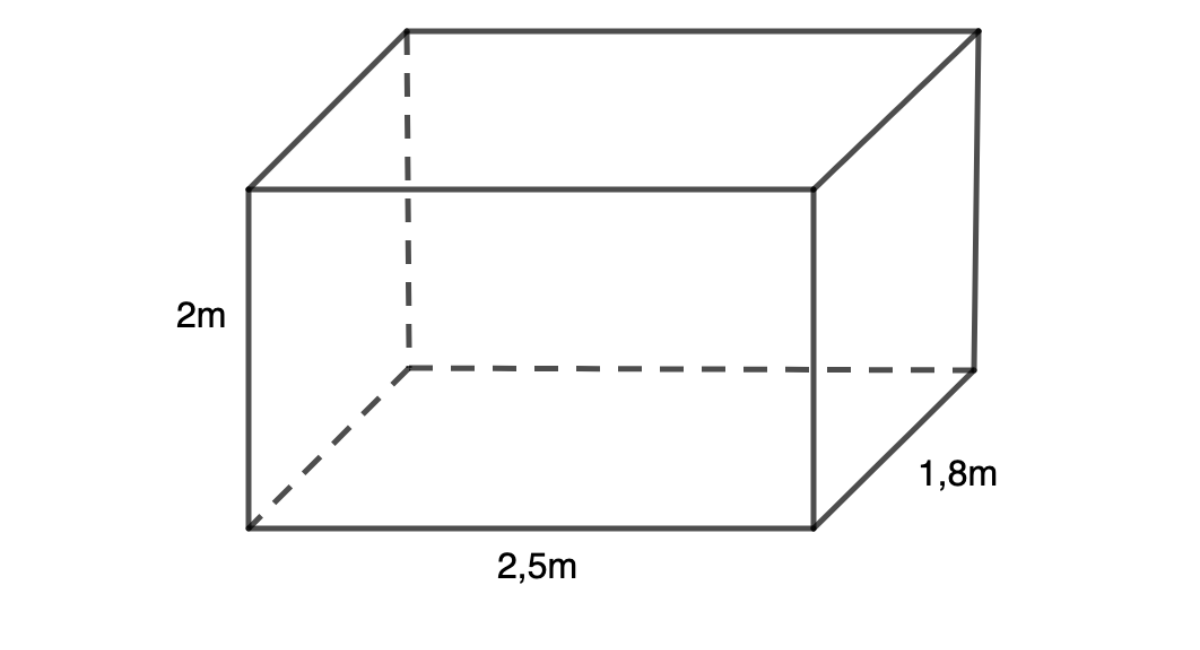
Ví dụ 2: Một bể cá hình hộp chữ nhật có chiều dài 80 cm, chiều rộng 50 cm và chiều cao 40 cm. Tính thể tích của bể cá.
Giải:
Thể tích của bể cá là:
V = a x b x h = 80 cm x 50 cm x 40 cm = 160.000 cm3
Tính cạnh của hộp chữ nhật khi đã biết thể tích
Từ công thức V = a x b x h, ta có thể suy ra các công thức tính từng kích thước khi biết hai kích thước còn lại:
Chiều dài (a): a = V / (b x h)
Chiều rộng (b): b = V / (a x h)
Chiều cao (h): h = V / (a x b)
Ví dụ 1: Tính chiều rộng của một hộp chữ nhật có thể tích 240cm^3, chiều dài 4cm và chiều cao 5cm.
Giải:
Áp dụng công thức tính chiều rộng: b = V / (a x h) = 240 / (4x 5) = 12cm.
Vậy chiều rộng của hộp chữ nhật là 12cm.
Ví dụ 2: Một bể cá hình hộp chữ nhật có chiều dài 60cm, chiều rộng 30cm và thể tích là 108000cm^3. Tính chiều cao của bể cá.
Giải:
Áp dụng công thức tính chiều cao: h = V / (a x b) = 108000 / (60 x 30) = 60cm.
Vậy chiều cao của bể cá là 60cm.

Tính thể tích hình hộp chữ nhật bị cắt bỏ một phần
Thể tích của một vật thể là số đo lượng không gian mà vật thể đó chiếm giữ. Để tính thể tích hộp chữ nhật bị cắt bỏ một phần, ta cần thực hiện các bước sau:
Bước 1: Tính thể tích của phần hộp chữ nhật ban đầu bằng cách sử dụng công thức V = a x b x h.
Bước 2: Tính thể tích của phần bị cắt bỏ tùy theo hình dạng của hình đó.
Bước 3: Tính thể tích hộp chữ nhật còn lại bằng cách lấy thể tích phần hộp chữ nhật ban đầu trừ đi thể tích phần bị cắt bỏ.
Bài 1: Tính thể tích của một hộp chữ nhật có chiều dài 12cm, chiều rộng 6cm và chiều cao 3cm nếu một phần của hộp bị cắt bỏ có dạng hình hộp chữ nhật có chiều dài 4cm, chiều rộng 3cm và chiều cao 3cm.
Giải:
Thể tích phần hộp chữ nhật ban đầu: V1 = 12cm x 6cm x 3cm = 216cm^3.
Thể tích phần bị cắt bỏ: V2 = 4cm x 3cm x 3cm = 36cm^3.
Thể tích hộp chữ nhật còn lại: V = V1 - V2 = 216cm^3 - 36cm^3 = 180cm^3.
Vậy thể tích hộp chữ nhật còn lại là 180cm^3.
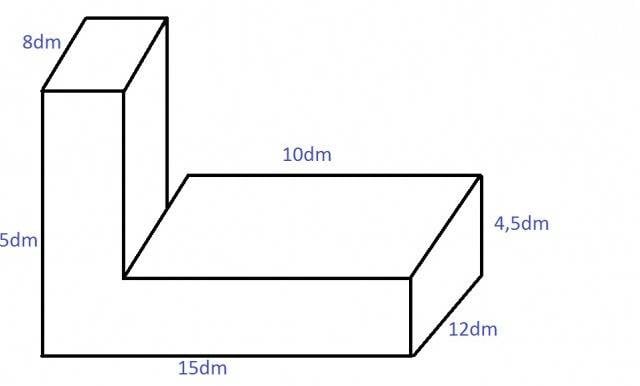
Bài 2: Một khối gỗ hình hộp chữ nhật có kích thước 8cm x 5cm x 3cm. Người ta cắt đi một phần khối gỗ có dạng hình lập phương cạnh 2cm. Tính thể tích phần còn lại.
Giải:
Thể tích phần hộp chữ nhật ban đầu: V1 = 8cm x 5cm x 3cm = 120cm^3.
Tính thể tích phần bị cắt bỏ: V2 = 2cm x 2cm x 2cm = 8cm^3.
Tính thể tích phần gỗ còn lại: V = V1 - V2 = 120cm^3 - 8cm^3 = 112cm^3.
Vậy thể tích phần gỗ còn lại là 112cm^3.
Tính thể tích hình hộp chữ nhật có một lỗ hình tròn
Tương tự như cách giải trên, tuy nhiên, phần V2 có công thức rõ ràng hơn.
Thể tích hộp chữ nhật ban đầu: V1 = a x b x h.
Thể tích phần hình trụ: V2 = πr^2h.
Muốn tính thể tích hình hộp chữ nhật còn lại: V = V1 - V2.
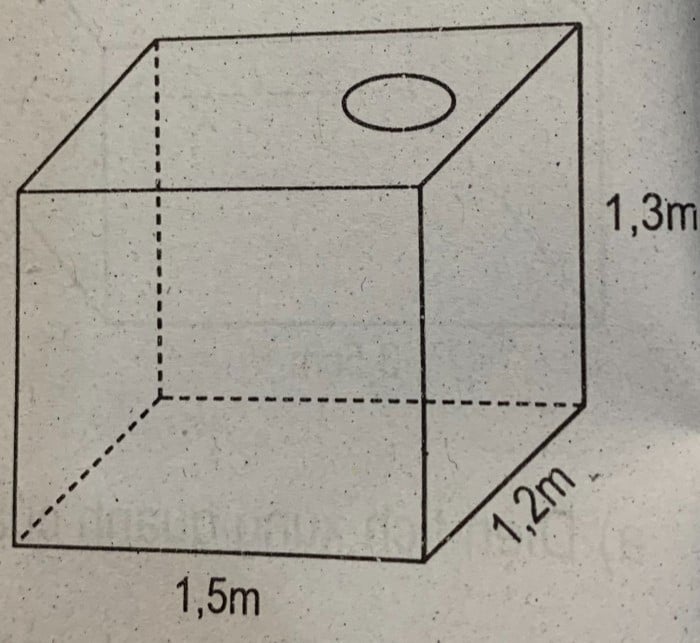
Ví dụ minh họa: Tính thể tích của một hộp chữ nhật có chiều dài 10cm, chiều rộng 8cm và chiều cao 6cm nếu một lỗ hình tròn bán kính 2cm bị đục ra khỏi nó.
Giải:
Thể tích khối hình hộp chữ nhật ban đầu: V1 = 10cm x 8cm x 6cm = 480cm^3.
Tính thể tích phần hình trụ: V2 = π x 2^2 x 6 = 24π cm^3 ≈ 75.4 cm^3 (lấy giá trị π ≈ 3.14).
Thể tích hộp chữ nhật còn lại: V = V1 - V2 = 480cm^3 - 75.4 cm^3 ≈ 404.6 cm^3.
Vậy thể tích hộp chữ nhật còn lại là 404.6 cm^3.
Các bài tập thể tích hình hộp chữ nhật lớp 5
Dạng 1: Tính thể tích hình hộp chữ nhật khi biết các kích thước.
Bài 1: Một viên gạch xây dựng có kích thước 20cm x 10cm x 5cm. Tính thể tích của viên gạch đó.
Bài 2: Một căn phòng có chiều dài 5m, chiều rộng 4m và chiều cao 3m. Tính thể tích của căn phòng đó.
Bài 3: Một bể cá hình hộp chữ nhật có chiều dài 60cm, chiều rộng 30cm và chiều cao 40cm. Bể cá đang chứa 1/2 thể tích nước. Tính lượng nước trong bể (bằng lít).
Bài 4: Một khối gỗ hình hộp chữ nhật có kích thước 25cm x 15cm x 10cm. Người ta cắt khối gỗ thành các khối lập phương nhỏ có cạnh 5cm. Hỏi có thể cắt được bao nhiêu khối lập phương từ khối gỗ đó?
Bài 5: Một thùng hàng hình hộp chữ nhật có thể chứa được tối đa 360 hộp sữa có kích thước 6cm x 4cm x 3cm. Kích thước tối đa của thùng hàng này là bao nhiêu cm (giả sử chiều dài, chiều rộng và chiều cao của thùng hàng là các số nguyên dương)?
Dạng 2: Tính một trong ba kích thước của hình hộp chữ nhật khi biết thể tích hình hộp chữ nhật và hai kích thước còn lại.
Bài 6: Tính chiều rộng của một hộp chữ nhật có thể tích 240cm^3, chiều dài 4cm và chiều cao 5cm.
Bài 7: Một bể cá hình hộp chữ nhật có chiều dài 60cm, chiều rộng 30cm và thể tích là 108000cm^3. Tính chiều cao của bể cá.
Bài 8: Một viên gạch xây dựng có kích thước 20cm x 10cm x h. Thể tích của viên gạch là 800cm^3. Tính chiều cao của viên gạch.
Bài 9: Một căn phòng có chiều dài 5m, chiều rộng 4m và thể tích là 80m^3. Tính chiều cao của căn phòng.
Bài 10: Một bể bơi hình hộp chữ nhật có chiều dài 25m, chiều rộng 15m và chiều cao là 3m. Người ta bơm thêm nước vào bể để lượng nước trong bể chiếm 80% thể tích bể. Tính lượng nước bơm thêm vào bể (bằng mét khối).
Dạng 3: Tính thể tích hình hộp chữ nhật bị cắt bỏ một phần.
Bài 11: Tính thể tích của một hộp chữ nhật có chiều dài 12cm, chiều rộng 6cm và chiều cao 3cm nếu một phần của hộp bị cắt bỏ có dạng hình hộp chữ nhật có chiều dài 4cm, chiều rộng 3cm và chiều cao 3cm.
Bài 12: Một khối gỗ hình hộp chữ nhật có kích thước 8cm x 5cm x 3cm. Người ta cắt đi một phần khối gỗ có dạng hình lập phương cạnh 2cm. Tính thể tích phần gỗ còn lại.
Bài 13: Một chiếc hộp sữa hình hộp chữ nhật có chiều dài 10cm, chiều rộng 7cm và chiều cao 5cm. Hộp sữa này bị móp méo một phần, phần móp méo có dạng hình hộp chữ nhật có chiều dài 3cm, chiều rộng 2cm và chiều cao 1cm. Tính thể tích phần sữa còn lại trong hộp.
Bài 14: Một khối bê tông hình hộp chữ nhật có kích thước 20cm x 15cm x 10cm. Người ta khoét một lỗ hình trụ có bán kính đáy 5cm và chiều cao 10cm vào khối bê tông. Tính thể tích phần bê tông còn lại.
Bài 15: Một bể nước hình hộp chữ nhật có chiều dài 2.5m, chiều rộng 1.5m và chiều cao 1m. Bể có một lỗ thoát nước hình trụ ở đáy bể có bán kính đáy 5cm. Tính thể tích nước trong bể khi mực nước đạt 80% chiều cao của bể.
Bài 16: Một khối xốp hình hộp chữ nhật có chiều dài 20cm, chiều rộng 10cm và chiều cao 8cm. Người ta cắt khối xốp thành hai phần bằng một mặt phẳng vuông góc với đáy, sao phần cắt bằng 1/3 khối xốp ban đầu. Hãy tính thể tích phần còn lại.

Đường chéo của hình hộp chữ nhật có tính chất như thế nào?
Hai đường chéo của mỗi mặt hình chữ nhật vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường chéo. Trong trường hợp đặc biệt khi hình hộp chữ nhật là hình lập phương, tất cả các cạnh đều bằng nhau và các đường chéo cũng bằng nhau.
Khi cắt hình hộp chữ nhật theo đường chéo, ta sẽ chia hình hộp thành bốn tam giác cân. Bốn tam giác này có hai cạnh bằng nhau (là một nửa cạnh đáy của hình hộp chữ nhật) và một cạnh khác bằng đường chéo của hình hộp chữ nhật.
Dạng tính thể tích hình hộp chữ nhật là một dạng toán học cơ bản nhưng có vai trò quan trọng trong nhiều lĩnh vực. Việc nắm vững công thức và phương pháp tính toán thể tích hình hộp chữ nhật giúp bạn có thể giải quyết các bài toán liên quan một cách hiệu quả và chính xác.



























