Công thức tính thể tích hình trụ và bài tập vận dụng

Công thức tính thể tích hình trụ và các dạng bài tập thường gặp kèm lời giải chi tiết

Tính thể tích hình trụ là dạng bài tập đơn giản nhưng xuất hiện rất nhiều trong các đề thi và đề kiểm tra. Thể tích hình trụ được tính bằng công thức: V = Sđáy.h. Trong đó, Sđáy là diện tích mặt đáy, h là chiều cao của hình lăng trụ đó. Ứng dụng của hình trụ dễ thấy ở lĩnh vực xây dựng hay thiết kế sản phẩm.

Các công thức tính thể tích hình trụ

Thể tích hình trụ là công thức có cùng bản chất với hình lăng trụ nói chung.

Tính thể tích hình trụ cơ bản

Thể tích hình trụ được tính bằng cách nhân diện tích đáy của hình trụ với chiều cao của nó. Công thức tổng quát để tính thể tích của một hình trụ là:

V = Sđáy.h

Xem thêm:

Công thức tính thể tích hình nón áp dụng với mọi dạng bài tập

Trong đó:

V là thể tích của lăng trụ.
Sđáy là diện tích đáy.
h là chiều cao của lăng trụ.

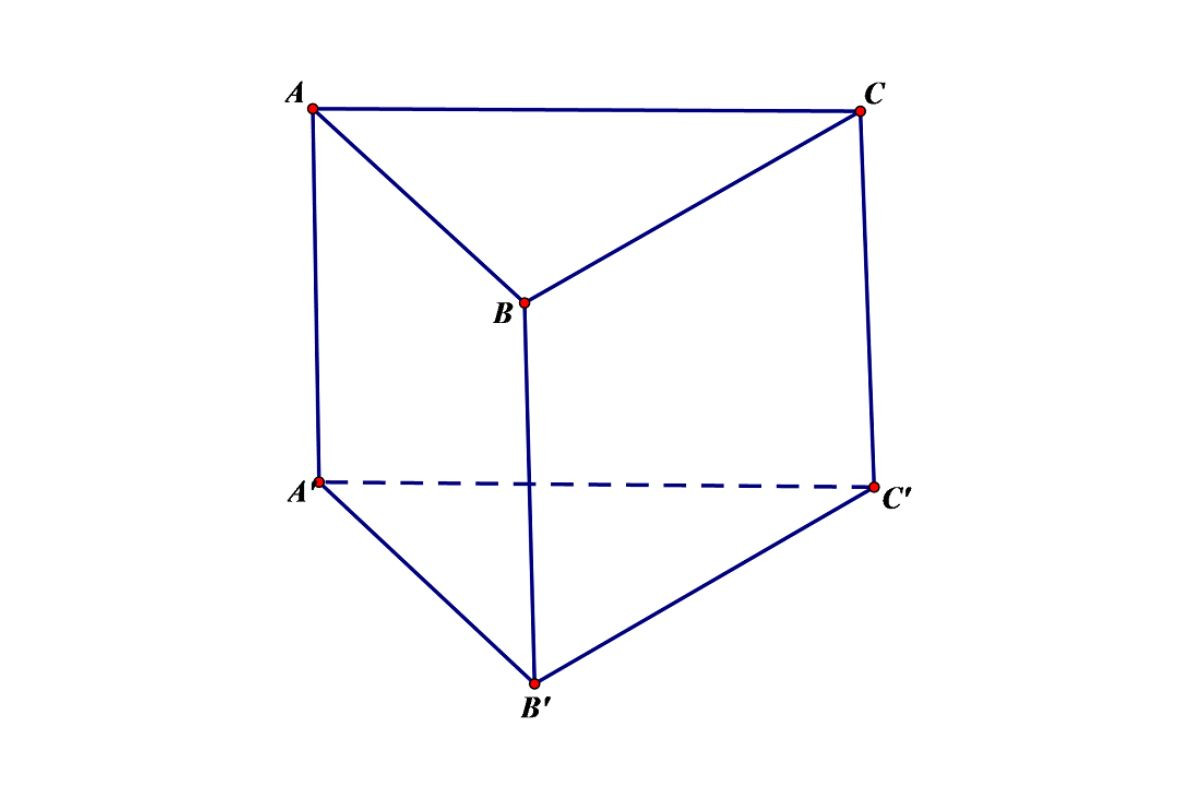
Thể tích hình lăng trụ đứng tam giác

Để tính thể tích của một hình lăng trụ đứng có đáy tam giác, bạn cần biết diện tích của tam giác đáy và chiều cao của lăng trụ.

Công thức tính thể tích của một hình lăng trụ đứng có đáy là một tam giác là:

V= Stam giác đáy.h

Trong đó:

V là thể tích của lăng trụ.
Stam giác đáy là diện tích đáy, được tính bằng công thức Stam giác đáy = 1/2.độ dài đáy.htam giác
h là chiều cao của lăng trụ.

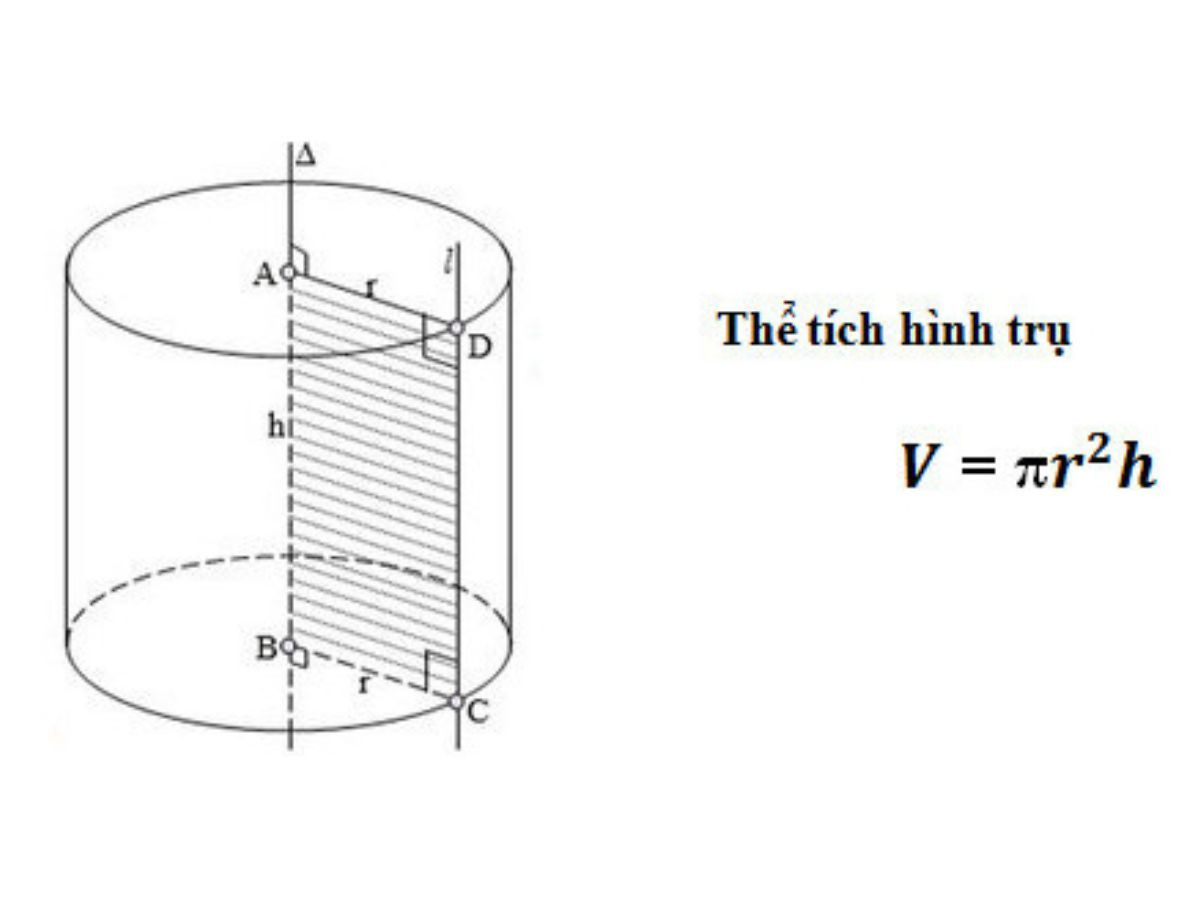
Tính thể tích hình trụ tròn

Để tính thể tích hình trụ tròn, bạn cần biết diện tích mặt đáy của hình trụ đó. Ta có công thức tổng quát tính thể tích hình trụ tròn như sau:

V=π.r².h

Trong đó:

V là thể tích của hình trụ.
π là một hằng số xấp xỉ bằng 3.14.
r là bán kính đáy hình trụ.
h là chiều cao của hình trụ.

Các công thức khác liên quan đến hình trụ

Một số đề bài cho sẵn về thể tích hình trụ, khi đó, bạn sẽ phải thực hành tính các chỉ số liên quan như bán kính đáy, diện tích đáy, chiều cao. Dưới đây là một số công thức hữu ích bạn có thể tham khảo để áp dụng vào bài tập:

Tính bán kính đáy của hình trụ

Để tính bán kính đáy của hình trụ khi đã biết thể tích và chiều cao, bạn có thể sử dụng lại công thức thể tích của hình trụ và giải phương trình để tìm r.

Công thức thể tích của hình trụ tròn là: V = π.r².h.

Suy ra, để tìm bán kính r, ta thực hiện phép tính:

r = √V/π.h

Tính diện tích hình tròn đáy

Để tính diện tích hình tròn đáy của lăng trụ tròn, bạn có thể tích của lăng trụ tính bằng công thức: V = π.r².h.

Từ đó, ta có công thức tính diện tích hình tròn đáy là:

Sđáy=π .r² =V/h

Tính chiều cao của hình trụ

Khi có thể tích hình trụ và diện tích đáy, bạn có thể suy ra công thức tính chiều cao hình trụ như sau:

h= V/Sđáy

*Chiều cao hình lăng trụ được tính bằng thể tích chia diện tích đáy*

Các dạng bài tập về thể tích của khối trụ tròn xoay

Thể tích khối trụ tròn xoay là phần kiến thức dễ học và áp dụng. Dưới đây là những dạng bài tập thường gặp trong quá trình học các công thức tính thể tích khối trụ:

Dạng 1: Tính bán kính đáy của khối trụ tròn xoay

Cụ thể về phương pháp giải dạng toán tính bán kính đáy khối trụ tròn:

Khi có diện tích hình tròn đáy, ta có công thức: r=√Sđáy.π
Khi đề cho thể tích và chiều cao khối trụ tròn, có công thức r=√V/π.h

Dạng 2: Tính diện tích đáy hình trụ tròn

Đối với bài toán tính diện tích đáy của khối trụ tròn, một số trường hợp có thể xảy ra như:

Khi có thể tích và chiều cao, diện tích đáy có thể tính bằng: Sđáy=V/h.
Khi đề bài cho sẵn bán kính đáy, ta có thể tính diện tích đáy bằng công thức tính hình tròn: Sđáy=π.r².

Dạng 3: Tính chiều cao hình trụ

Chiều cao của hình trụ có thể tính được khi biết thể tích khối trụ và bán kính đáy/diện tích đáy bằng công thức:

h= V/Sđáy= V/π.r²

Tổng hợp bài tập tính thể tích hình trụ có lời giải

Sau khi nắm rõ công thức tính thể tích hình trụ và các chỉ số liên quan, bạn có thể củng cố kiến thức bằng cách làm các bài tập sau đây:

Câu 1: Công thức nào dưới đây dùng để tính thể tích hình lăng trụ đứng?

A. 2.Cđáy.h

B. Cđáy.h

C. 2.Sđáy.h

D. Sđáy.h

Đáp án đúng là: D

Công thức đúng dùng để tính thể tích của hình lăng trụ đứng là: Sđáy.h.

Câu 2: Chiều cao hình lăng trụ đứng tứ giác ABCD.A’B’C’D’ có thể tích là 160 cm3, đáy hình vuông có cạnh cạnh 5 cm là (gợi ý tính bằng công cụ máy tính casio 580 online):

A. 6,4 cm.

B. 8 cm.

C. 10 cm.

D. 32 cm.

Đáp án đúng là: A

Diện tích đáy của lăng trụ đứng tứ giác ABCD.A’B’C’D’ là:

5 x 5 = 25 (cm2)

Chiều cao của lăng trụ đứng tứ giác ABCD.A’B’C’D’ là:

160 : 25 = 6,4 (cm)

Các ứng dụng trong thực tế

Thể tích hình trụ không chỉ là một khái niệm toán học mà còn có ứng dụng rộng rãi trong nhiều lĩnh vực của đời sống và kỹ thuật. Dưới đây là một số ứng dụng tiêu biểu:

Xây dựng: Tính toán kích thước của cột trụ, ống dẫn nước và các thành phần cấu trúc khác trong công trình.
Công nghiệp: Thiết kế và sản xuất các bộ phận máy móc như xi lanh, trục quay, bình chứa dầu khí.
Kỹ thuật môi trường: Tính toán dung tích của các bể chứa xử lý nước thải và chất thải rắn.
Khoa học vật liệu: Xác định kích thước và dung tích của các vật liệu dạng trụ để nghiên cứu tính chất vật lý.
Thiết kế sản phẩm: Tính toán thể tích và kích thước cho các sản phẩm dạng trụ như chai lọ, lon đồ uống.

*Hình trụ được ứng dụng nhiều trong quy trình sản xuất ống nhôm*

Có rất nhiều cách tính thể tích hình trụ, tuỳ thuộc vào dữ liệu đề bài cho. Công thức cơ bản nhất để tìm thể tích là: V = Sđáy.h. Công thức tính thể tích hình trụ được áp dụng rất nhiều trong thực tế cuộc sống trong kỹ thuật, công nghiệp, xây dựng. Để thành thạo các dạng bài tập về hình trụ, bạn cần ghi nhớ kỹ công thức và luyện tập tìm nhiều biến số khác nhau.