Hình Trụ là gì?
Trước khi đến với công thức tính diện tích toàn phần hình trụ, cùng tìm hiểu hình trụ là gì. Hình trụ là một hình học không gian được định nghĩa như sau:
- Hai mặt đáy: Là hai hình tròn bằng nhau và song song với nhau.
- Mặt xung quanh: Là một mặt cong được tạo thành bởi việc quay một hình chữ nhật quanh một cạnh cố định của nó. Cạnh cố định này được gọi là trục hình trụ.
- Chiều cao: Là khoảng cách giữa hai mặt đáy của hình trụ.
- Đường sinh: Là các đường thẳng nằm trên mặt xung quanh và vuông góc với hai mặt đáy.
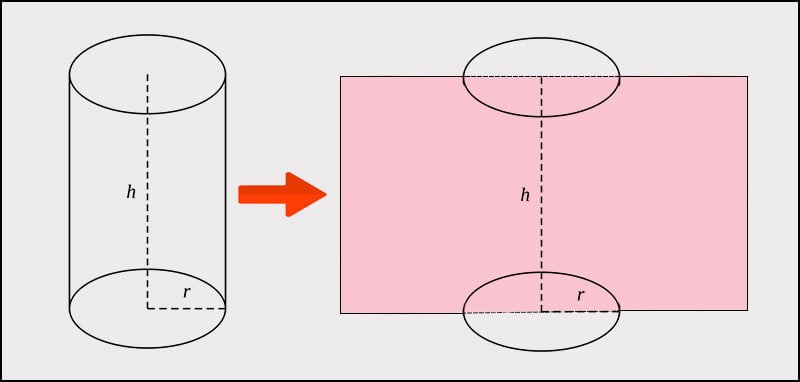
Công thức tính diện tích xung quanh hình trụ
Diện tích xung quanh (Sxq) của hình trụ được tính bằng công thức sau: Sxq = 2πrh
Trong đó:
- π (pi) là hằng số xấp xỉ bằng 3,14159.
- r là bán kính mặt đáy hình trụ (tính bằng đơn vị mét, cm, inch, v.v.).
- h là chiều cao hình trụ (tính bằng đơn vị mét, cm, inch, v.v.).
Giải thích công thức:
- Mặt xung quanh của hình trụ có thể được xem như là một hình chữ nhật được cuộn tròn lại.
- Chiều dài của hình chữ nhật bằng chu vi của đường tròn đáy, được tính bằng 2πr.
- Chiều rộng của hình chữ nhật bằng chiều cao của hình trụ, được tính bằng h.
- Diện tích của hình chữ nhật bằng tích của chiều dài và chiều rộng, được tính bằng 2πrh.
Ví dụ:
- Một hình trụ có bán kính đáy r = 5 cm và chiều cao h = 10 cm. Diện tích xung quanh của hình trụ này là:
Sxq = 2πrh = 2π(5 cm)(10 cm) = 100π cm²
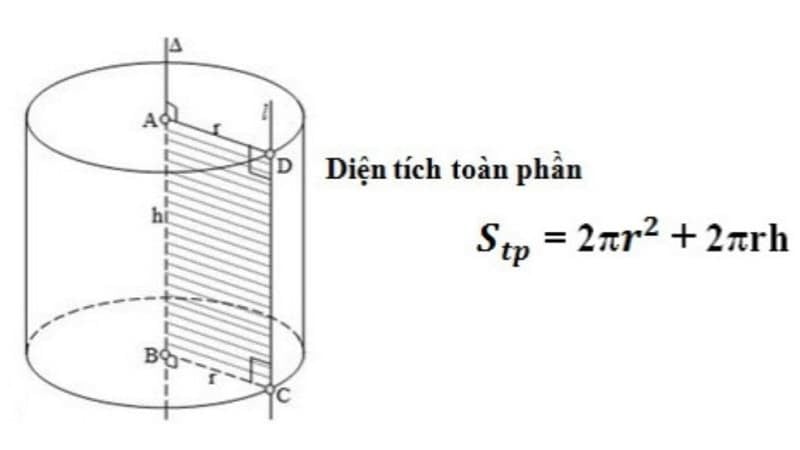
Công thức tính diện tích toàn phần hình trụ
Diện tích toàn phần hình trụ được tính bằng công thức sau: Stp = 2πrh + 2πr²
Trong đó:
- π (pi) là hằng số xấp xỉ bằng 3,14159.
- r là bán kính mặt đáy hình trụ (tính bằng đơn vị mét, centimet, inch, v.v.).
- h là chiều cao hình trụ (tính bằng đơn vị mét, centimet, inch, v.v.).
Giải thích công thức:
- Diện tích toàn phần của hình trụ bao gồm diện tích xung quanh (Sxq) và diện tích hai mặt đáy (Sđáy).
- Diện tích xung quanh được tính bằng công thức Sxq = 2πrh, như đã giải thích ở trên.
- Diện tích mỗi mặt đáy bằng diện tích hình tròn, công thức Sđáy = πr².
- Diện tích toàn phần được tính bằng tổng diện tích xung quanh và diện tích hai mặt đáy, công thức Stp = Sxq + 2Sđáy = 2πrh + 2πr².
Ví dụ: Một hình trụ có bán kính đáy r = 5 cm và chiều cao h = 10 cm. Diện tích toàn phần của hình trụ này là: Stp = 2πrh + 2πr² = 2π(5 cm)(10 cm) + 2π(5 cm)² = 100π cm² + 50π cm².
Các dạng bài tập liên quan đến tính diện tích hình trụ
Các dạng bài tập liên quan đến tính diện tích hình trụ hay diện tích toàn phần hình trụ thường gặp bao gồm:
Bài 1: Một hình trụ có diện tích xung quanh Sxq = 314 cm² và bán kính đáy r = 5 cm. Tính chiều cao h của hình trụ.
Bài 2: Một hình trụ có diện tích toàn phần Stp = 628 cm² và bán kính đáy r = 7 cm. Tính chiều cao h của hình trụ.
Bài 3: Một hình trụ có thể tích V = 1570 cm³ và bán kính đáy r = 6 cm. Tính chiều cao h của hình trụ.
Hướng dẫn giải bài toán 1:
Áp dụng công thức tính diện tích xung quanh của hình trụ: Sxq = 2πrh và công cụ máy tính casio online
Ta có: 314 cm² = 2π(5 cm)h
Giải phương trình ta được: h = 314 cm² / (2π x 5 cm) ≈ 10 cm
Vậy chiều cao h của hình trụ là 10 cm.
Tính bán kính đáy của hình trụ
Bài 1: Một hình trụ có diện tích xung quanh Sxq = 314 cm² và chiều cao h = 10 cm. Tính bán kính đáy r của hình trụ.
Bài 2: Một hình trụ có diện tích toàn phần Stp = 628 cm² và chiều cao h = 4 cm. Tính bán kính đáy r của hình trụ.
Bài 3: Một hình trụ có thể tích V = 1570 cm³ và chiều cao h = 14 cm. Tính bán kính đáy r của hình trụ.
Hướng dẫn giải bài toán 1:
Áp dụng công thức tính diện tích xung quanh của hình trụ: Sxq = 2πrh
Ta có: 314 cm² = 2π(10cm)r
Giải phương trình ta được: r ≈ 5 cm
Vậy bán kính đáy r của hình trụ là 5 cm.
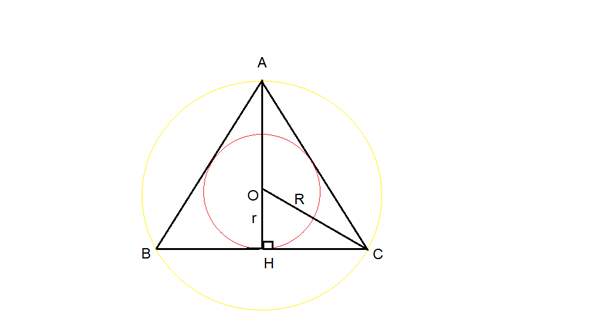
Đáy là đường tròn ngoại tiếp tam giác, tính diện tích hình trụ
Cho một hình trụ có đáy là đường tròn ngoại tiếp tam giác ABC. Biết độ dài các cạnh của tam giác ABC lần lượt là a, b,c. Hãy tính diện tích toàn phần (Stp) và diện tích xung quanh (Sxq) của hình trụ đó.
Đáy là đường tròn nội tiếp tam giác, tính diện tích hình trụ
Cho một hình trụ có đáy là đường tròn nội tiếp tam giác ABC. Biết độ dài các cạnh của tam giác ABC lần lượt là a, b, c. Hãy tính diện tích toàn phần (Stp) và diện tích xung quanh (Sxq) của hình trụ đó.
Bài toán ứng dụng công thức tính diện tích toàn phần hình trụ trong thực tế
Bài toán: Một công ty sản xuất thùng nước bằng tôn dạng hình trụ có chiều cao h = 80 cm và bán kính đáy r = 30 cm. Hỏi công ty đó cần bao nhiêu mét vuông tôn để sản xuất 1000 thùng nước như vậy?
Giải:
Diện tích toàn phần của mỗi thùng nước là: Stp = 2πrh + 2πr² = 2π(30 cm)(80 cm) + 2π(30 cm)² = 1508 cm²
Diện tích tôn cần thiết để sản xuất 1000 thùng nước là: S = 1508 cm² x 1000 = 1 508 000 cm²
Đổi diện tích sang mét vuông: S = 1 508 000 cm² / (100 cm/m)² = 150,8 m²
Vậy, công ty đó cần 150,8 mét vuông tôn để sản xuất 1000 thùng nước như vậy.
Tính diện tích sơn cần thiết để sơn toàn bộ mặt ngoài của một cái bể nước dạng hình trụ:
Bài toán: Một bể nước dạng hình trụ có bán kính đáy r = 1,5 m và chiều cao h = 2 m. Hỏi cần bao nhiêu lít sơn để sơn toàn bộ mặt ngoài của bể nước đó (không tính đáy)?
Giải: Diện tích cần sơn là diện tích xung quanh của hình trụ, được tính bằng: Sxq = 2πrh = 2π(1,5 m)(2 m) = 9,42 m²
Lượng sơn cần thiết được tính bằng: V = Sxq x n
Trong đó: n là số lớp sơn. Giả sử ta sơn 2 lớp sơn. Vậy, lượng sơn cần thiết là: V = 9,42 m² x 2 = 18,84 m³
Đổi thể tích sang lít: V = 18,84 m³ x 1000 lít/m³ = 18 840 lít
Vậy, cần 18 840 lít sơn để sơn toàn bộ mặt ngoài của bể nước đó (không tính đáy).
Tính diện tích vải cần thiết để may một cái lều hình trụ:
Bài toán: Một đội du lịch muốn may một cái lều hình trụ có chiều cao h = 2,5 m và đường kính đáy d = 4 m. Hỏi cần bao nhiêu mét vuông vải để may cái lều đó (không tính phần đáy)?
Giải: Bán kính đáy của lều là r = d/2 = 4 m/2 = 2 m.
Diện tích cần thiết để may cái lều là diện tích xung quanh của hình trụ, cộng với diện tích hai mặt đáy hình tròn.Tuy nhiên, trong bài toán này ta không cần tính diện tích đáy.
Diện tích xung quanh của hình trụ được tính bằng:
Sxq = 2πrh = 2π(2 m)(2,5 m) = 31,42 m²
Vậy, cần 31,42 mét vuông vải để may cái lều đó (không tính phần đáy).

Những ứng dụng của hình trụ trong đời sống
Hình trụ có rất nhiều ứng dụng trong đời sống, bao gồm:
- Kiến trúc và xây dựng: Hình trụ thường được các kỹ sư công trường dùng để thiết kế các cột trụ, ống khói cũng như các cấu trúc tròn khác trong rất nhiều những công trình kiến trúc. Sự mạnh mẽ cùng với khả năng chịu lực đặc trưng của hình trụ khiến nó luôn trở thành sự lựa chọn hàng đầu trong rất nhiều dự án. Ví như như thiết kế cầu thang xoắn ốc giúp tiết kiệm diện tích và tạo điểm nhấn cho các công trình nhà ở, mặt bằng kinh doanh,...
- Công nghiệp: Trong ngành công nghiệp nói riêng, khối trụ được dùng trong sản xuất các bộ phận, máy móc như các trục, ống dẫn, các bình chứa áp lực cao, nhờ vào hình dáng đặc trưng giúp chịu được sức ép lớn.
- Giao thông vận tải: Các bộ phận trụ tròn được sử dụng rộng rãi trong ngành công nghiệp ô tô và hàng không, từ khung xe đến thân máy bay, nhờ vào khả năng phân bố lực tốt và giảm sức cản của không khí. Nhiều bộ phận của xe máy, ô tô như piston, trục truyền động,... có dạng hình trụ.

- Đồ gia dụng: Nhiều đồ gia dụng dạng hình trụ như bình nóng lạnh, thân cái đèn, các loại chai lọ mỹ phẩm có thiết kế hình trụ nhìn vừa thẩm mỹ vừa tiện lợi trong cách bảo quản và sử dụng.
- Đồ chơi: Hình trụ được sử dụng để làm đồ chơi cho trẻ em như: xếp hình khối, lồng quay. Nó có hình dạng đẹp mắt và kích thích trí tưởng tượng của trẻ. Ví dụ như: bộ xếp hình khối trụ, lồng quay hình trụ,...
- Trang trí: Hình trụ được sử dụng để trang trí nhà cửa, văn phòng, cửa hàng... vì nó có hình dạng sang trọng và hiện đại. Ví dụ như: đèn LED hình trụ, lọ hoa hình trụ, trụ trang trí,...

Ngoài ra, hình trụ còn được sử dụng trong nhiều lĩnh vực khác như:
- Y học: Hình trụ được dùng làm ống nghiệm, ống tiêm, máy chụp X-quang, v.v.
- Khoa học: Vệ tinh nhân tạo thường có dạng hình trụ để tối ưu hóa hiệu quả thu thập tín hiệu và truyền thông. Tàu ngầm cũng có dạng hình trụ giúp giảm sức cản của nước, di chuyển dễ dàng dưới nước. Ngoài ra trong lĩnh vực này hình trụ còn được ứng dụng để tạo ra kính hiển vi, máy ly tâm, máy gia tốc,...
- Nghệ thuật: tượng điêu khắc, tranh vẽ, đồ gốm sứ,...
Có thể thấy, hình trụ là một hình học có nhiều ứng dụng quan trọng trong đời sống. Nhờ có những ưu điểm về độ bền, khả năng chịu lực cao và tính thẩm mỹ, hình trụ được sử dụng trong nhiều lĩnh vực khác nhau. Biết về cách tính diện tích toàn phần hình trụ giúp ích cho chúng ta rất nhiều trong đời sống hằng ngày.



























