Q là tập hợp số gì? Ví dụ?
Khi tìm hiểu về các tập số trong toán học, nhiều người thắc mắc Q là tập hợp số gì và có những tính chất gì. Theo quy ước toán học, Q là ký hiệu của tập hợp các số hữu tỉ. Số hữu tỉ có thể được biểu diễn dưới dạng phân số với tử và mẫu là các số nguyên và mẫu số khác 0.
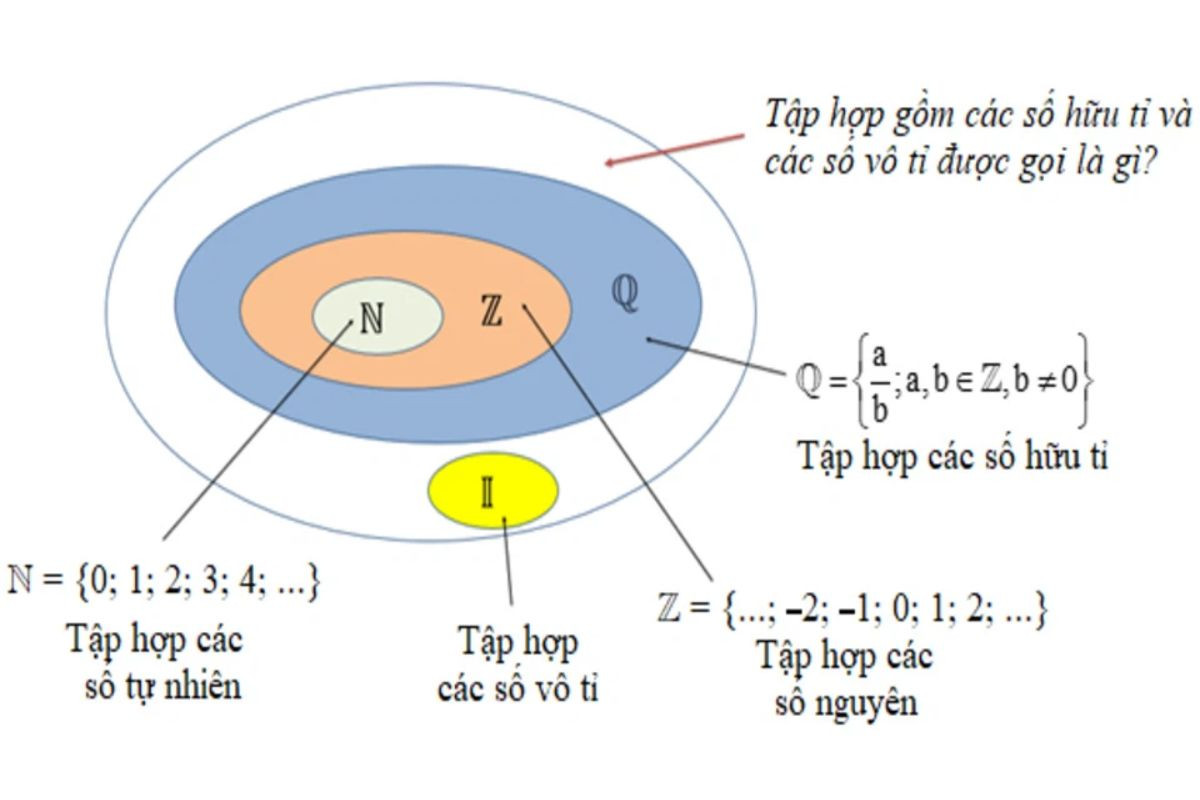
Tập hợp số hữu tỉ bao gồm cả các số nguyên (vì mọi số nguyên đều có thể viết dưới dạng phân số), các số thập phân hữu hạn và các số thập phân vô hạn tuần hoàn. Các số hữu tỉ xuất hiện rất nhiều trong toán học và trong các ứng dụng thực tế như đo lường và tính toán các tỷ lệ.
Tập hợp Q có vai trò quan trọng trong số học và lý thuyết số, đồng thời cũng là nền tảng để xây dựng các khái niệm phức tạp hơn trong toán học như các số thực và số phức. Do đó, việc tìm hiểu Q là tập hợp số gì và nắm rõ các tính chất của tập hợp Q là rất quan trọng.
Ví dụ về tập hợp Q:
- Các số nguyên: -3, 0, 5
- Các phân số: ½, ⅚
- Các số thập phân hữu hạn: 0.75, -2.5, 1.2
- Các số thập phân vô hạn tuần hoàn: 0.3333…, -1.6666…, 2.14657696….
Q là tập hợp những số gì?
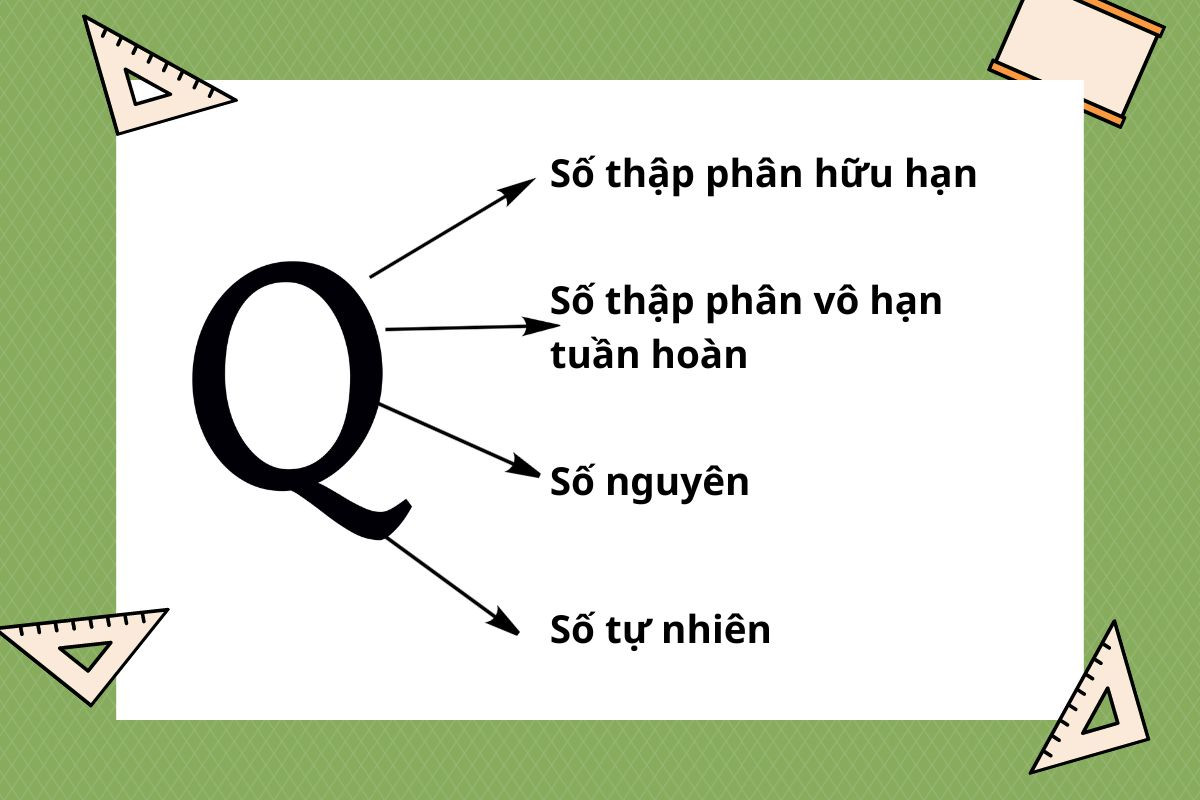
Sau khi biết được Q là tập hợp số gì, dưới đây là những số thuộc tập hợp Q mà bạn có thể tham khảo:
Số thập phân hữu hạn
Các số thập phân hữu hạn thuộc tập hợp Q. Số thập phân hữu hạn là số có thể được viết dưới dạng một phân số, trong đó tử số và mẫu số đều là các số nguyên. Do đó số thập phân hữu hạn cũng là số hữu tỉ.
Ví dụ:
- Số thập phân 0.75 có thể viết dưới dạng phân số là ¾
- Số thập phân -2.5 có thể được viết dưới dạng phân số là -5/2
- Số thập phân 1.2 có thể viết dưới dạng phân số là 6/5
Số thập phân vô hạn tuần hoàn
Khi tìm hiểu Q là tập hợp số gì, bạn sẽ biết số thập phân vô hạn tuần hoàn cũng thuộc tập hợp Q. Số thập phân vô hạn tuần hoàn là số có phần thập phân lặp lại một chu kỳ nhất định và có thể được biểu diễn dưới dạng một phân số với tử số và mẫu số là các số nguyên.
Ví dụ:
- Số thập phân 0.3333… được viết dưới dạng phân số là ⅓
- Số thập phân 0.6666… được viết dưới dạng phân số là ⅔
- Số thập phân 1.142857142857… được viết dưới dạng phân số 8/7
Tập hợp số nguyên
Các số nguyên cũng thuộc tập hợp số hữu tỉ Q. Số nguyên là số không có phần thập phân và có thể được biểu diễn dưới dạng phân số với mẫu số là 1. Đây là trường hợp đặc biệt của số hữu tỉ.
Ví dụ:
- Số nguyên 5 được viết dưới dạng phân số là 5/1
- Số nguyên -3 được viết dưới dạng phân số là -3/1
- Số nguyên 0 được viết dưới dạng phân số là 0/1
Tập hợp số tự nhiên
Các số tự nhiên được ký hiệu là tập N, sau khi biết Q là tập hợp số gì, bạn sẽ biết số tự nhiên cũng thuộc tập hợp Q. Số tự nhiên là các số nguyên không âm bắt đầu từ 0, 1, 2, 3, và tiếp tục như vậy. Các số này cũng có thể được biểu diễn dưới dạng phân số với mẫu số là 1, do đó chúng thỏa mãn định nghĩa của số hữu tỉ.
Ví dụ:
- Số tự nhiên 0 được viết dưới dạng phân số là 0/1
- Số tự nhiên 2 được viết dưới dạng phân số là 2/1
- Số tự nhiên 5 được viết dưới dạng phân số là 5/1
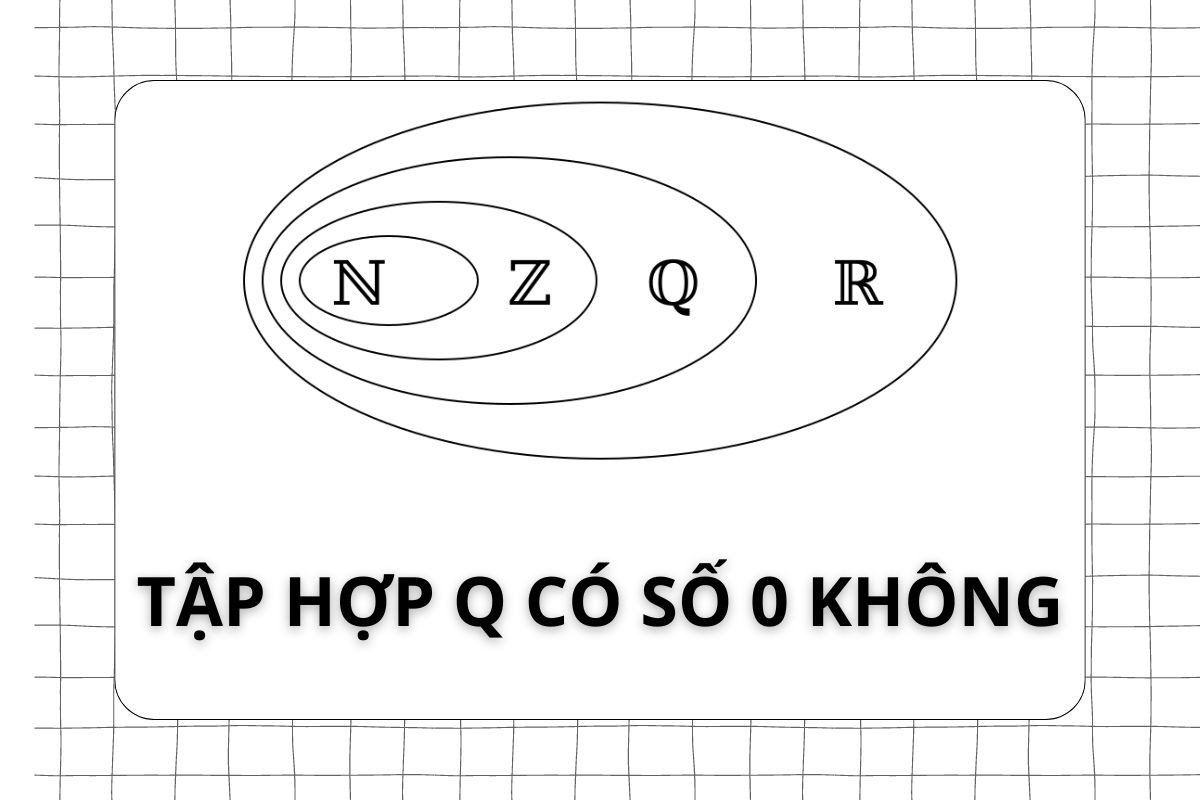
Tập hợp Q có bao gồm số 0 không?
Khi tìm hiểu Q là tập hợp số gì, nhiều người thắc mắc không biết tập hợp Q có bao gồm số 0 không. Thực tế, tập hợp Q bao gồm cả số 0. Số 0 là số hữu tỉ vì nó có thể được biểu diễn dưới dạng phân số là 0/1.
Tính chất của tập hợp số Q trong toán học
Tìm hiểu Q là tập hợp số gì và nắm rõ các tính chất của tập hợp Q sẽ giúp bạn dễ dàng vận dụng tính chất của số hữu tỉ để thực hiện các phép toán và giải quyết các dạng toán có liên quan. Dưới đây là những tính chất cơ bản của tập hợp Q trong toán học:

- Nếu a và b là hai số hữu tỉ thì tổng a+b hay hiệu a- b cũng là số hữu tỉ.
- Nếu a và b là hai số hữu tỉ thì a.b và a:b(với b # 0) cũng cho ra kết quả là một số hữu tỉ.
- Tập hợp Q chứa rất nhiều loại số khác nhau, từ các số nguyên đến các số thập phân hữu hạn và các số thập phân vô hạn tuần hoàn.
- Mọi số nguyên đều là một số hữu tỉ. Nói cách khác, mọi số nguyên có thể được biểu diễn dưới dạng một phân số với mẫu số là 1.
- Q là tập hợp con của tập hợp R vì mọi số hữu tỉ đều là số thực.
- Tập hợp Q chứa số vô hạn số hữu tỉ. Điều này bao gồm cả các số nguyên, các số thập phân hữu hạn, và các số thập phân vô hạn tuần hoàn.
Nắm vững các tính chất trên giúp bạn vận dụng vào việc tính toán, so sánh số hữu tỉ một cách nhanh chóng và chính xác.
Cách so sánh hai số hữu tỉ trong toán học
Trong toán học, để so sánh hai số hữu tỉ, bạn sẽ sử dụng các phép so sánh thông thường như <, >, =. Để so sánh hai số hữu tỉ, bạn cần biết Q là tập hợp số gì, các tập hợp con của Q và tính chất của tập hợp Q.
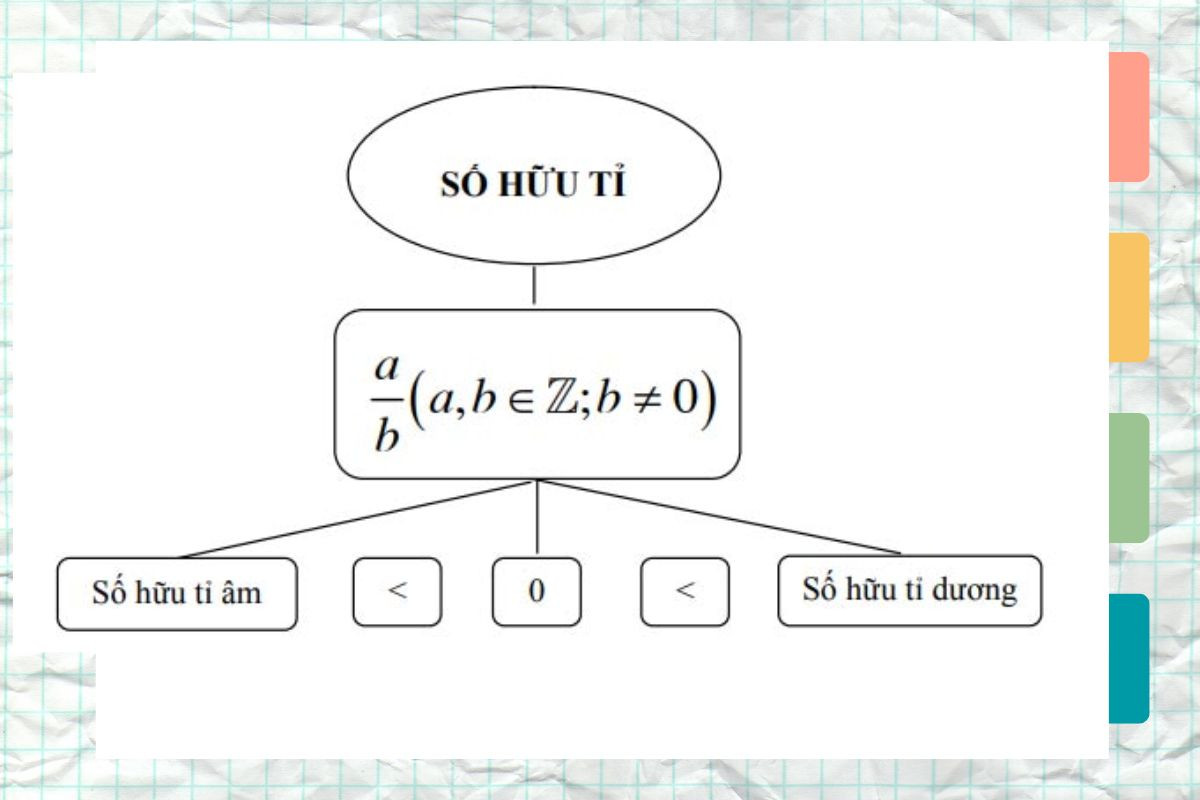
Trước khi so sánh hai số hữu tỉ, bạn cần quy đồng mẫu số để chuyển chúng về dạng 2 phân số có cùng mẫu số. Từ đó giúp cho việc so sánh 2 số hữu tỉ được thực hiện dễ dàng hơn. Để quy đồng mẫu số của hai phân số, ta nhân tử và mẫu của mỗi số với mẫu số của số kia.
Sau khi có cùng mẫu số, ta chỉ cần so sánh tử số của hai số. Số nào có tử số lớn hơn thì số đó lớn hơn. Nếu tử số bằng nhau, chúng ta sẽ tiếp tục so sánh dựa trên mẫu số. Nếu tử số bằng nhau, chúng ta sẽ so sánh mẫu số. Số nào có mẫu số nhỏ hơn thì số đó lớn hơn. Nếu cả tử số và mẫu số đều bằng nhau, hai số đó là bằng nhau.
Ví dụ: So sánh hai phân số ⅓ và ⅖
- Bước 1: Quy đồng mẫu số hai phân số trên với mẫu số chung là 15. Ta có ⅓ = 5/15, ⅖ = 6/15.
- Bước 2: So sánh tử số của hai phân số sau khi quy đồng mẫu số: Vì 5 < 6 nên 5/15 < 6/15 hay nói cách khác ⅓ < ⅖
Một số dạng toán về tập hợp số Q trong toán học
Có nhiều loại bài toán trong toán học liên quan đến tập hợp các số hữu tỉ Q. Để giải được các dạng toán này, bạn cần biết Q là tập hợp số gì và các tính chất của tập hợp Q trong toán học. Dưới đây là một số dạng toán liên quan đến số hữu tỉ:

Dạng 1: Bài toán phân số:
- Tìm phân số tối giản của một phân số.
- Tính tổng, hiệu, tích và thương của các phân số.
- So sánh hai phân số.
- Chuyển phân số thành số thập phân
Ví dụ: Tìm phân số tối giản của 24/36
Cách giải:
- Bước 1: Tìm ước chung lớn nhất (UCLN) của tử số và mẫu số: UCLN(24, 36) = 12.
- Bước 2: Chia cả tử số và mẫu số cho UCLN: 24/26 = 2/13
Dạng 2: Bài toán số học:
- Tìm ước số chung lớn nhất (UCLN) và bội số chung nhỏ nhất (BCNN) của hai hoặc nhiều số hữu tỉ.
- Phân tích một số thành các thừa số nguyên tố.
- Tìm số lượng các số hữu tỉ nằm trong một khoảng cho trước.
Ví dụ: Tìm UCLN và BCNN của 18 và 24.
Cách giải:
- Bước 1: Phân tích số thành các thừa số nguyên tố: 18 = 2 x 3^2, 24 = 2^3 x 3
- Bước 2: ƯCLN là tích các thừa số nguyên tố chung với bội số nhỏ nhất của mỗi thừa số. Do đó ƯCLN (18, 24) = 2 x 3 = 6
- Bước 3: BCNN là tích các thừa số nguyên tố trong hai số, mỗi thừa số chỉ lấy số mũ lớn nhất. Do đó, BCNN (18, 24) = 2^3 x 3^2 = 72
Dạng 3: Bài toán giải tích:
- Xác định giới hạn của một dãy số hữu tỉ.
- Tính tích phân của một hàm số hữu tỉ trên một đoạn cho trước.
Dạng 4: Bài toán đại số:
- Giải phương trình hoặc hệ phương trình có ẩn số là số hữu tỉ.
- Tìm các số hữu tỉ thỏa mãn điều kiện cụ thể.
- Tìm điều kiện để một phương trình hoặc bất phương trình có nghiệm hữu tỉ.
Ví dụ: Giải phương trình 2x - 3 = 7
Cách giải:
2x - 3 = 7
=> 2x = 7 +3 = 10
=> x = 10 : 2
=> x = 5
Vậy nghiệm của phương trình 2x - 3 = 7 là x = 5
Dạng 5: Bài toán xác suất và thống kê:
- Tính xác suất của sự kiện liên quan đến các số hữu tỉ.
- Tính trung bình, phương sai của các biến ngẫu nhiên có giá trị là số hữu tỉ.
Ví dụ: Xác suất để một con xúc xắc 6 mặt được tung và ra số chia hết cho 3 là bao nhiêu?
Cách giải:
- Số lượng số chia hết cho 3 trên một xúc xắc 6 mặt là 2, 4 và 6.
- Tổng số kết quả có thể có là 6 (vì có 6 mặt xúc xắc).
- Xác suất được tính bằng số kết quả thuận lợi chia cho tổng số kết quả có thể có là 3/6 = ½
Việc nắm rõ Q là tập hợp số gì và các tính chất của tập hợp Q giúp bạn dễ dàng giải quyết các dạng toán liên quan đến phân số, phép tính với phân số. Bên cạnh đó, tập hợp Q không chỉ có ý nghĩa trong toán học mà còn có ứng dụng rộng rãi trong nhiều lĩnh vực như kỹ thuật, khoa học máy tính,... Vì vậy hiểu rõ Q là tập hợp các số gì là điều rất cần thiết.



























