Hình vuông là gì?
Hình vuông là một loại hình học phổ biến, xuất hiện không chỉ trong các bài toán học mà còn trong nhiều ứng dụng thực tế. Trước khi tìm hiểu về công thức tính diện tích hình vuông, hãy cùng khám phá khái niệm và những đặc điểm nổi bật của hình này.
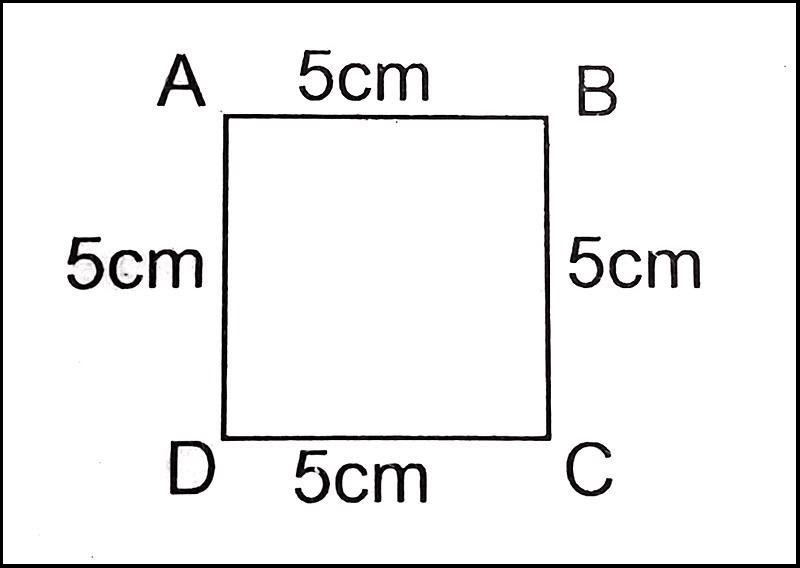
Hình vuông là một loại tứ giác đặc biệt với 4 cạnh bằng nhau. Điểm khác biệt chính giữa hình vuông và các hình tứ giác khác là:
- Hình vuông có 4 cạnh đều nhau.
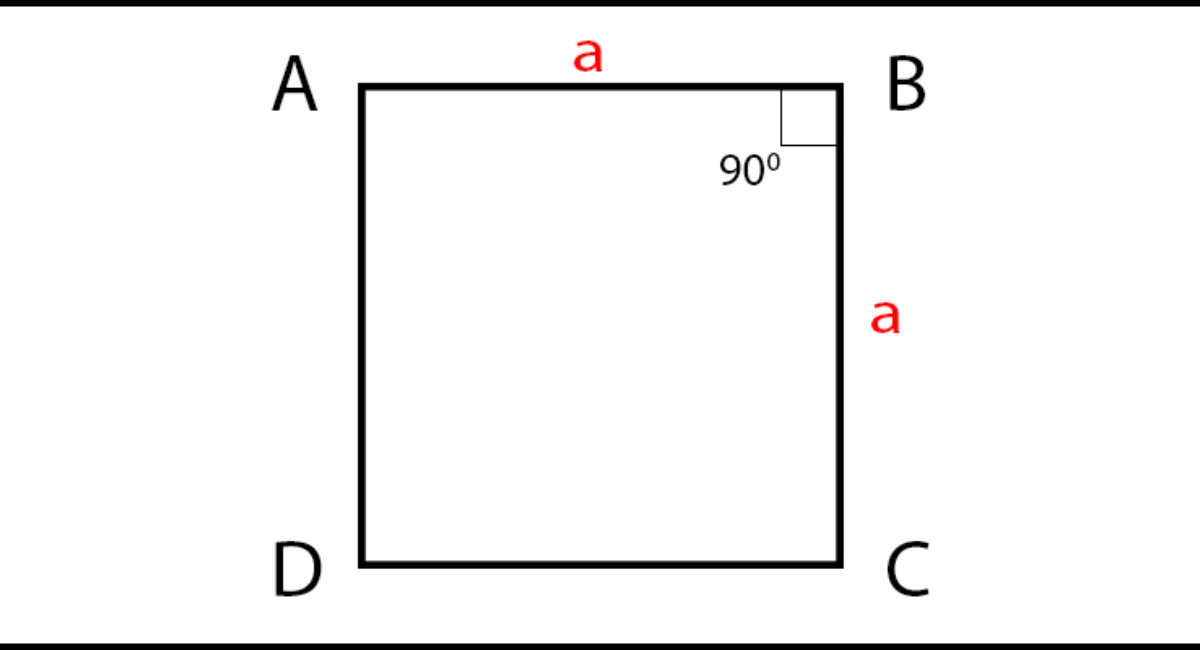
- Tất cả các góc của hình vuông đều là góc vuông, tức là mỗi góc đều có 90 độ.
- Hai cặp cạnh đối diện của hình vuông vừa bằng nhau vừa song song với nhau.
Khi một tứ giác thỏa mãn các điều kiện này, ta có thể gọi nó là hình vuông.
Tính chất của hình vuông
Mỗi hình vuông đều có các tính chất sau:
- Hai đường chéo của hình vuông có độ dài bằng nhau và cắt nhau tại trung điểm của chúng. Đồng thời, chúng cắt nhau tại một góc vuông.
- Đường tròn nội tiếp và đường tròn ngoại tiếp của hình vuông có cùng tâm, trùng với điểm giao của hai đường chéo.
- Mỗi đường chéo sẽ chia hình vuông thành hai tam giác bằng nhau.
- Hình vuông có các tính chất chung của các hình tứ giác đặc biệt khác như hình bình hành, hình thoi và hình chữ nhật.
Dấu hiệu nhận biết hình vuông
Dựa vào các dấu hiệu sau, bạn có thể nhận biết được hình tứ giác có phải là hình vuông hay không:
- Nếu là một hình chữ nhật có hai cạnh kề bằng nhau, thì đó là hình vuông.
- Nếu là hình chữ nhật mà hai đường chéo của nó vuông góc với nhau, thì đó cũng là hình vuông.
- Nếu là hình thoi mà có một góc vuông hoặc hai đường chéo của nó có độ dài bằng nhau thì cũng có thể xác định đó là hình vuông.
Công thức diện tích hình vuông
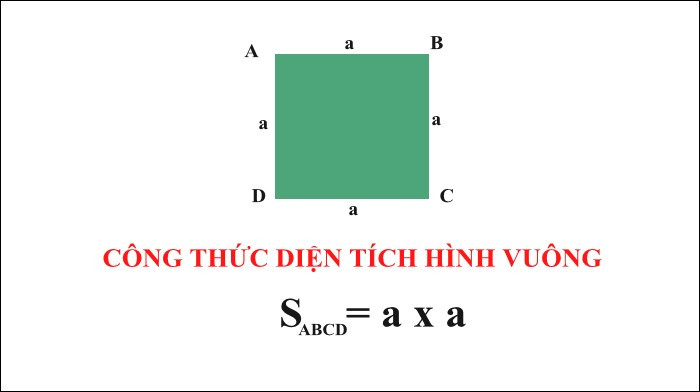
Diện tích hình vuông được xác định bằng cách nhân chiều dài của các cạnh với nhau. Do các cạnh hình vuông bằng nhau, nên chỉ cần biết độ dài của một cạnh là có thể tính được diện tích toàn bộ hình vuông.
Công thức
Gọi a là độ dài cạnh của hình vuông và S là diện tích của hình vuông, ta có công thức sau: S=a×a
Ví dụ
Sau khi đã hiểu rõ cách tính diện tích hình vuông, hãy thực hành một số bài tập sau để ghi nhớ công thức:
Ví dụ 1: Tính diện tích của tứ giác ABCD có dạng hình vuông, biết độ dài 1 cạnh là 40cm.
Lời giải:
Để tính diện tích của hình vuông ABCD, ta áp dụng công thức:
Diện tích (S) = cạnh x cạnh = a x a
Với cạnh a = 40cm, ta có:
S = a x a = 40cm x 40cm = 1600cm²
Vậy diện tích của tứ giác ABCD là 400cm².
Ví dụ 2: Chu vi của một lớp học bằng 200m, hãy tính diện tích của lớp học này biết lớp có dạng hình vuông.
Lời giải:
Áp dụng công thức tính chu vi của hình vuông: Chu vi = 4 x Độ dài cạnh
Với chu vi = 200m, ta có:
200 = 4 x a => a = 50m
Vậy một cạnh của lớp học có độ dài là 45m. Lúc này, ta áp dụng công thức để tính diện tích: S = a x a => S = 45m x 45m = 2.025m²
Vậy diện tích của lớp học có hình dạng hình vuông là 2.025m². (tính theo công cụ máy tính online casio fx-580vn plus)
Một số phương pháp tính diện tích hình vuông
Hình vuông - một trong những hình học cơ bản và phổ biến nhất, có lẽ chính vì tính đơn giản và dễ hình dung của nó mà chúng ta thường ngỡ rằng tính toán diện tích của hình vuông là một công việc vô cùng đơn giản. Tuy nhiên, khi đi sâu vào nghiên cứu, chúng ta sẽ nhận thấy rằng tính diện tích của hình vuông có rất nhiều phương pháp và kỹ thuật khác nhau, mỗi cách tiếp cận đều có những ưu điểm và nhược điểm riêng.
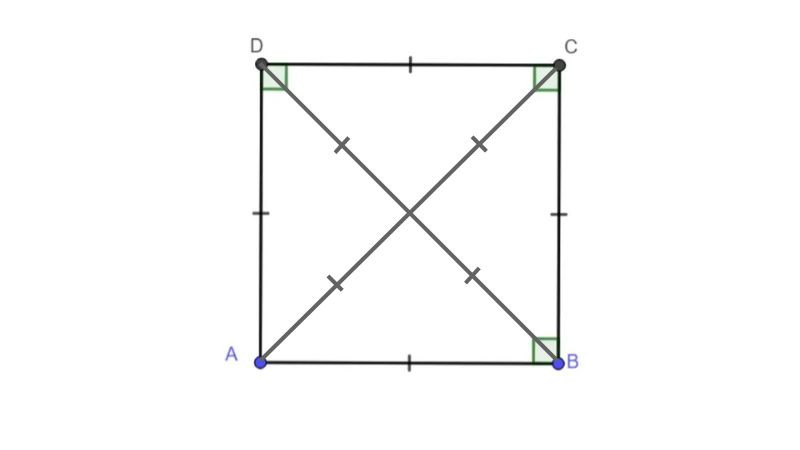
Tính diện tích hình vuông bằng tổng diện tích của 2 tam giác đường chéo
Ngoài việc sử dụng công thức S = a x a (với a là độ dài cạnh), chúng ta còn có thể tính diện tích hiện vuông bằng tổng diện tích của 2 tam giác được tạo ra khi kẻ một đường chéo trên hình vuông.
Trong hình vuông, tất cả các cạnh đều có độ dài bằng nhau và tất cả các góc đều có độ lớn là 90 độ. Khi kéo một đường chéo, nó sẽ chia hình vuông thành hai tam giác vuông có diện tích bằng nhau. Điều này có nghĩa là, nếu chúng ta vẽ một đường chéo trong hình vuông, sẽ có được hai diện tích hình tam giác vuông bằng nhau.
Gọi a là độ dài mỗi cạnh của hình vuông. Theo định lý Pytago-rơ, độ dài mỗi đường chéo sẽ bằng a * √2.
Diện tích của mỗi tam giác vuông là:
S_tam giác = (a * a * √2) / 2 = a^2 / 2
Vì có 2 tam giác vuông như vậy, nên tổng diện tích của chúng sẽ là:
Tổng diện tích của 2 tam giác = 2 * (a^2 / 2) = a^2
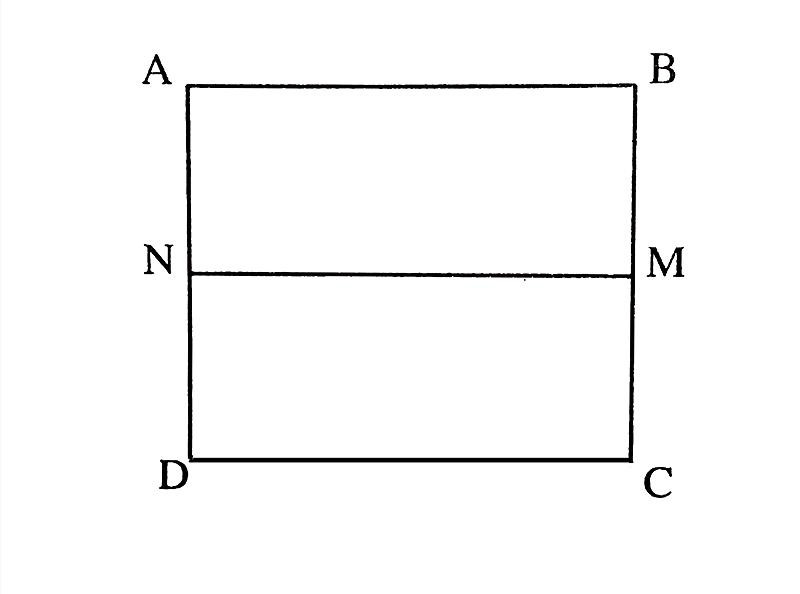
Tính diện tích hình vuông bằng tổng diện tích hai hình chữ nhật
Một hình vuông có thể được coi là tổng hợp của hai hình chữ nhật có cùng độ dài và chiều rộng. Điều này có nghĩa, nếu chia hình vuông thành hai phần theo một đường ngang, ta sẽ thu được hai hình chữ nhật có kích thước giống nhau.
Vậy, muốn tính diện tích hình vuông, chúng ta có thể tính tổng diện tích của hai hình chữ nhật đó. Mỗi hình chữ nhật có diện tích là tích của một cạnh nhân với cạnh còn lại. Do hình vuông có các cạnh bằng nhau nên diện tích của một hình chữ nhật sẽ bằng a x a/2, trong đó a là độ dài của cạnh của hình vuông.
Khi tính tổng diện tích của hai hình chữ nhật này, ta sẽ thu được diện tích của hình vuông. Do cả hai hình chữ nhật này có diện tích bằng nhau nên diện tích của hình vuông sẽ là gấp đôi diện tích của một trong số chúng.
Tóm lại, để tính diện tích của một hình vuông bằng tổng diện tích của hai hình chữ nhật, ta chỉ cần tính diện tích của một trong số chúng và nhân kết quả đó với 2.
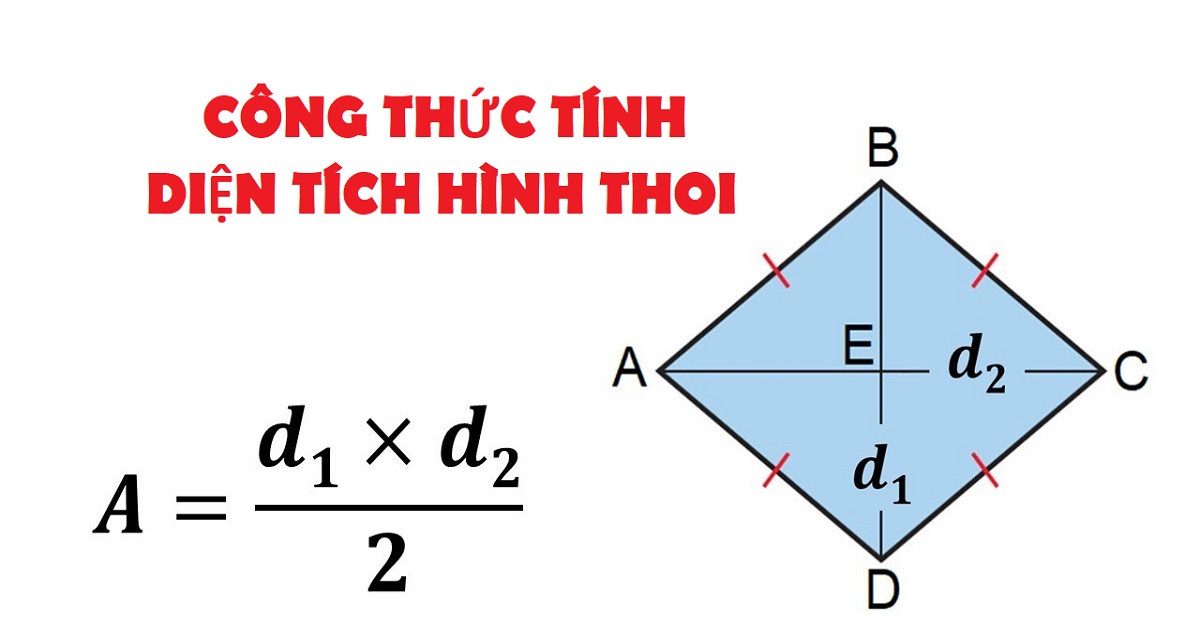
Tính diện tích của hình vuông bằng công thức tính diện tích hình thoi
Một hình vuông là một loại hình thoi có tất cả các cạnh bằng nhau và các góc trong đều là góc vuông. Vì vậy, ta hoàn toàn có thể tính diện tích của hình vuông bằng công thức tính diện tích hình thoi.
Công thức tính diện tích của một hình thoi là: S = (d1 x d2) / 2. Trong đó d1, d2 là độ dài hai đường chéo của hình thoi. Do đó, áp dụng công thức tính diện tích hình thoi cho hình vuông, ta có thể viết lại công thức đơn giản hơn như sau: S = (a * √2 * a * √2) / 2 = 2a^2 / 2 = a^2
Trong đó:
- Các cạnh của hình vuông đều bằng nhau, gọi là a
- Hai đường chéo giao nhau tạo thành hình thoi
- Độ dài mỗi đường chéo là a * √2
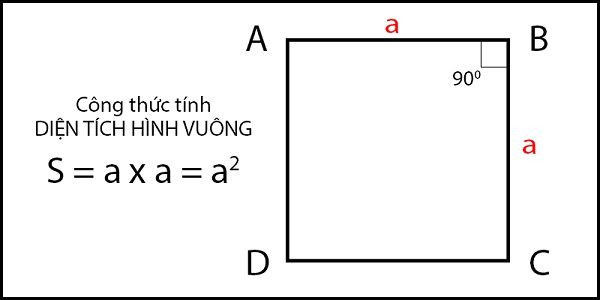
Tính diện tích hình vuông khi biết trước chu vi của nó
Trước hết, ta cần biết rằng một hình vuông có bốn cạnh bằng nhau. Vì vậy, để tính diện tích của nó khi biết chu vi, ta cần tìm độ dài của một cạnh trước.
Công thức tính chu vi của hình vuông là: Chu vi = 4 x Độ dài một cạnh. Từ đó, ta có thể suy ra độ dài của mỗi cạnh bằng cách chia chu vi cho 4.
Sau khi đã biết độ dài của một cạnh, ta có thể sử dụng công thức tính diện tích của hình vuông là Diện tích = Độ dài cạnh x Độ dài cạnh, hoặc đơn giản hơn là S = a^2, với a là độ dài của một cạnh hình vuông.
Một số lưu ý khi tính diện tích hình vuông
Khi tính toán diện tích của hình vuông, mặc dù công thức rất đơn giản nhưng vẫn cần lưu ý một số điều quan trọng để đảm bảo kết quả chính xác. Hiểu rõ những điểm cần lưu ý này sẽ giúp bạn tránh được những sai sót không đáng có khi giải các bài toán liên quan đến hình vuông.
- Đơn vị đo phải cùng một đơn vị: Khi tính toán, các cạnh của hình vuông phải được đo bằng cùng một đơn vị (ví dụ: cm, m). Nếu các đơn vị không đồng nhất, cần chuyển về một đơn vị chung như cm², m² trước khi thực hiện các phép tính.
- Sử dụng đơn vị đo diện tích: Khi tính diện tích của hình vuông, ta sử dụng đơn vị đo diện tích như cm² hoặc m². Không sử dụng đơn vị đo chiều dài như m, cm cho diện tích.
- Phân biệt công thức tính diện tích và chu vi: Cần phân biệt rõ ràng giữa công thức tính diện tích và chu vi của hình vuông. Hai công thức này thường bị nhầm lẫn, dẫn đến kết quả sai.
- Vận dụng tính chất của các hình tứ giác khác: Bạn có thể vận dụng công thức và tính chất của các hình tứ giác khác như hình chữ nhật, hình thang, hình thoi để tính ra diện tích của hình vuông nếu không có số liệu chiều dài cạnh được cung cấp trong đề bài.
Ứng dụng tính diện tích hình vuông trong thực tế
Hình vuông là một trong những hình học cơ bản và phổ biến nhất, với nhiều ứng dụng thực tế trong đời sống hàng ngày. Khả năng tính toán diện tích của hình vuông không chỉ là một kiến thức lý thuyết mà còn là một kỹ năng vô cùng hữu ích khi áp dụng vào các lĩnh vực khác nhau. Từ việc thiết kế nội thất đến xây dựng cơ sở hạ tầng, tính diện tích hình vuông đóng vai trò quan trọng trong nhiều hoạt động thực tiễn.
Một trong những ứng dụng phổ biến nhất của tính diện tích hình vuông là trong thiết kế và xây dựng. Khi xây nhà, tính toán diện tích sàn nhà, diện tích phòng, diện tích mặt bằng là rất quan trọng để đảm bảo sử dụng không gian hiệu quả và phù hợp với nhu cầu. Các kiến trúc sư thường sử dụng công thức tính diện tích hình vuông để ước tính chi phí xây dựng, thiết kế bố trí nội thất và đảm bảo tuân thủ các quy định về diện tích tối thiểu.
Ngoài ra, tính diện tích hình vuông cũng được ứng dụng rộng rãi trong lĩnh vực thiết kế đồ đạc và trang trí nội thất. Khi lựa chọn kích thước bàn, tủ, giường, sofa,... việc tính toán diện tích phòng và tỉ lệ hình vuông giúp đảm bảo sự hài hòa và thẩm mỹ.
Trong lĩnh vực quy hoạch đô thị, tính diện tích hình vuông cũng là một yếu tố quan trọng. Các quy hoạch về đường xá, công viên, khu dân cư thường sử dụng hình vuông như một đơn vị cơ bản để tính toán diện tích và bố trí hợp lý các công trình, tiện ích.
Ngoài những ứng dụng trên, tính diện tích hình vuông còn được áp dụng trong nhiều lĩnh vực khác như quản lý kho bãi, tính toán năng suất sản xuất, đo lường diện tích đất đai... Có thể nói, tính toán diện tích hình vuông là một kỹ năng vô cùng hữu ích trong cuộc sống hàng ngày.

Từ những ứng dụng cụ thể mà chúng ta vừa tìm hiểu, có thể thấy rõ tầm quan trọng của khả năng tính diện tích hình vuông trong thực tiễn. Nắm vững các công thức và kỹ năng tính toán diện tích hình vuông không chỉ là một yêu cầu về mặt học thuật mà còn là một công cụ vô cùng hữu dụng giúp bạn có thể dễ dàng áp dụng trong cuộc sống.
