Khái niệm và các tính chất của hình bình hành
Để giải quyết các bài toán liên quan đến chu vi hình bình hành thì việc nắm vững khái niệm và tính chất hình này là rất quan trọng. Đây là một tứ giác đặc biệt có các cặp cạnh đối song song với nhau. Nói cách khác, hai cặp cạnh đối của hình bình hành nằm trên cùng một mặt phẳng và không bao giờ giao nhau.
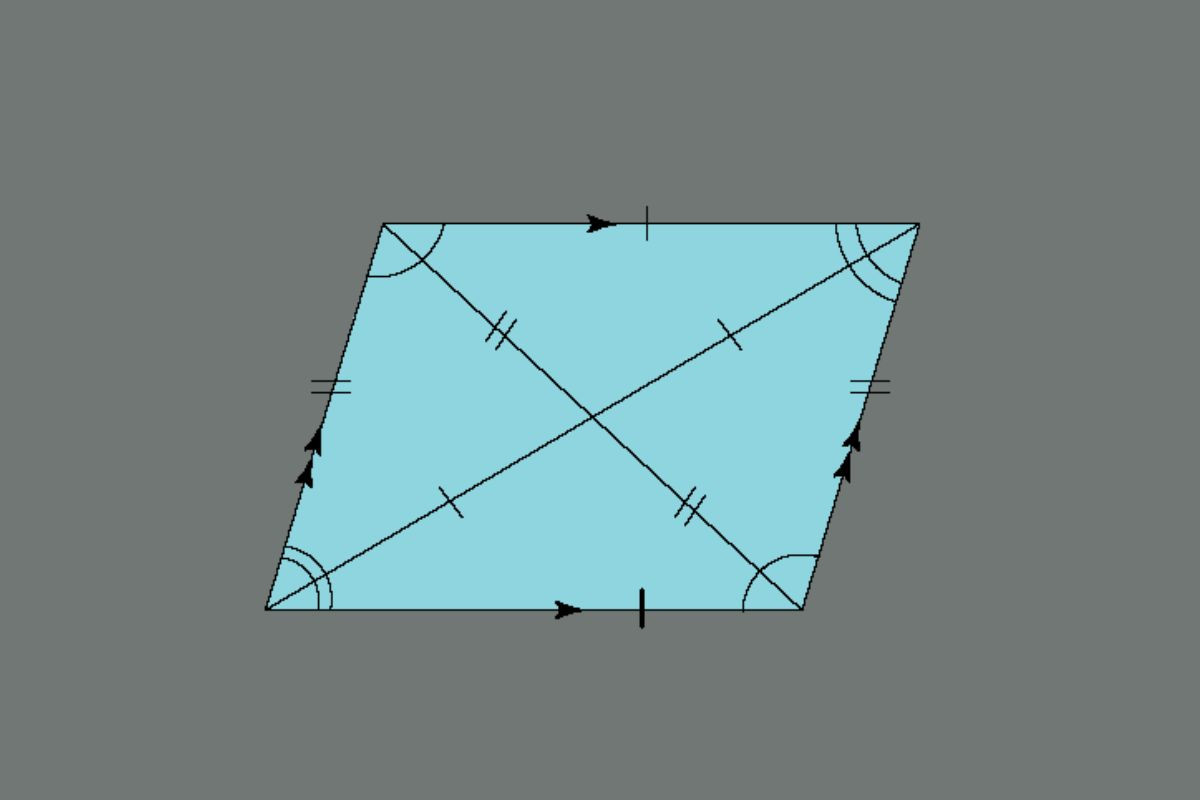
Chúng ta có thể xác định hình bình hành là tứ giác thỏa mãn một trong các điều kiện sau:
- Hai cặp cạnh đối song song và bằng nhau.
- Hai cặp cạnh đối bằng nhau.
- Hai đường chéo của một hình bình hành sẽ cắt nhau tại trung điểm của mỗi đường.
- Có hai góc đối bằng nhau.
- Tổng hai góc kề của một cạnh bằng 180°.
Giả sử, hình bình hành thường được ký hiệu là ABCD, trong đó AB || CD và AD || BC.
Ví dụ: Hình chữ nhật, hình thoi, hình vuông đều là những ví dụ về hình bình hành.
Ngoài ra, hình bình hành còn mang một số tính chất khác:
- Hai đường chéo vuông góc với nhau: ∠AIE = ∠BII = ∠CIE = ∠DII = 90° (chỉ đúng trong trường hợp hình bình hành là hình thoi).
- Hai đường chéo chia đôi hình bình hành thành hai tam giác bằng nhau.
- Đường trung tuyến của hình bình hành chia hình bình hành thành hai hình bình hành bằng nhau.
Công thức tìm chu vi hình bình hành
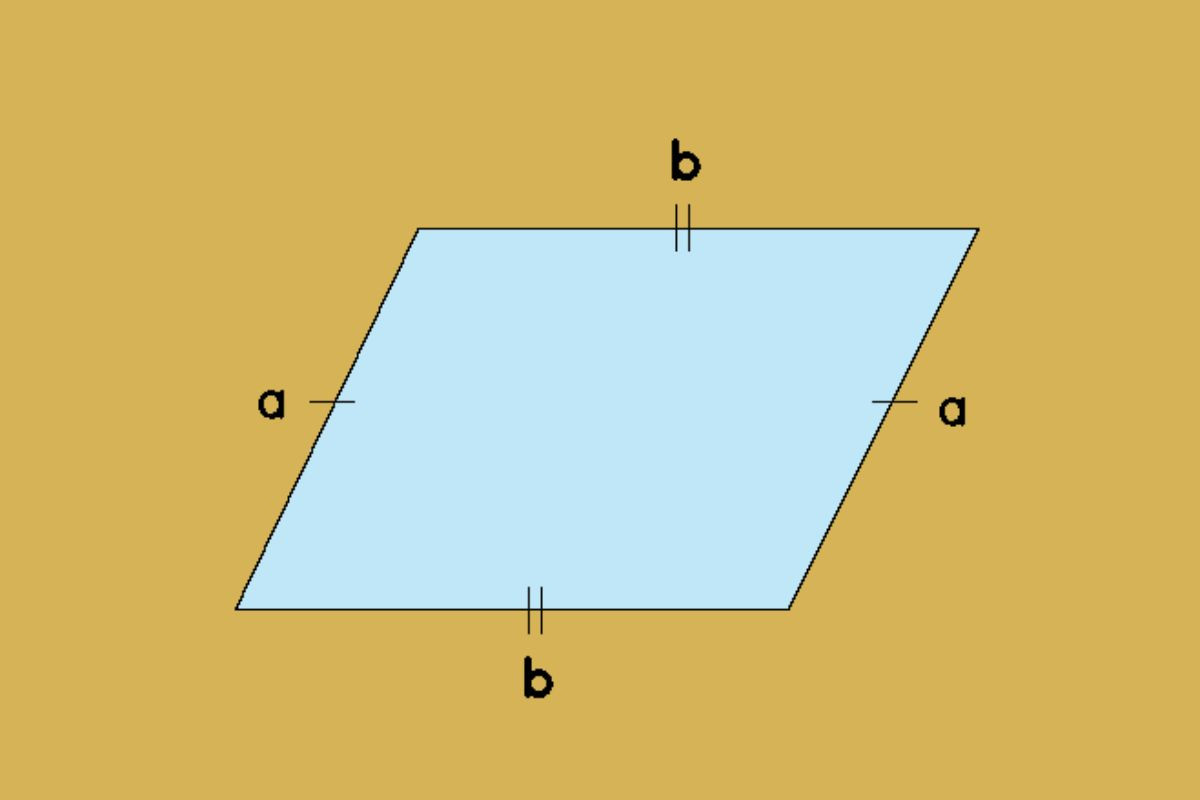
Chu vi của một hình bình hành có thể tính bằng cách cộng độ dài các cạnh của nó. Vì hình bình hành có hai cặp cạnh bằng nhau nên chu vi có thể được tính bằng công thức:
C = 2(a + b)
Trong đó:
C là chu vi hình bình hành (đơn vị: cm, m, km,...)
a và b là độ dài của hai cạnh kề nhau bất kỳ của hình bình hành (đơn vị: cm, m, km,...)
Ví dụ:
Cho một hình bình hành ABCD có hai cạnh AB và AD lần lượt dài 5 cm và 7 cm. Áp dụng công thức trên, ta có thể tính chu vi của hình bình hành ABCD như sau theo công cụ máy tính casio online 580:
C = 2(5 + 7) = 24 cm
Lưu ý:
- Công thức trên áp dụng cho tất cả các hình bình hành, bất kể kích thước hay hình dạng của chúng.
- Khi đo độ dài các cạnh của hình bình hành, cần sử dụng cùng một đơn vị đo (cm, m, km,...).
Các dạng bài tập tính chu vi hình bình hành thường gặp khác
Ngoài trường hợp phổ biến khi chúng ta có chiều dài của hai cạnh liền kề của hình bình hành đã nêu bên trên, học sinh có thể bắt gặp các dạng bài tập yêu cầu tính chu vi hình bình hành khi biết các điều kiện khác như dưới đây.
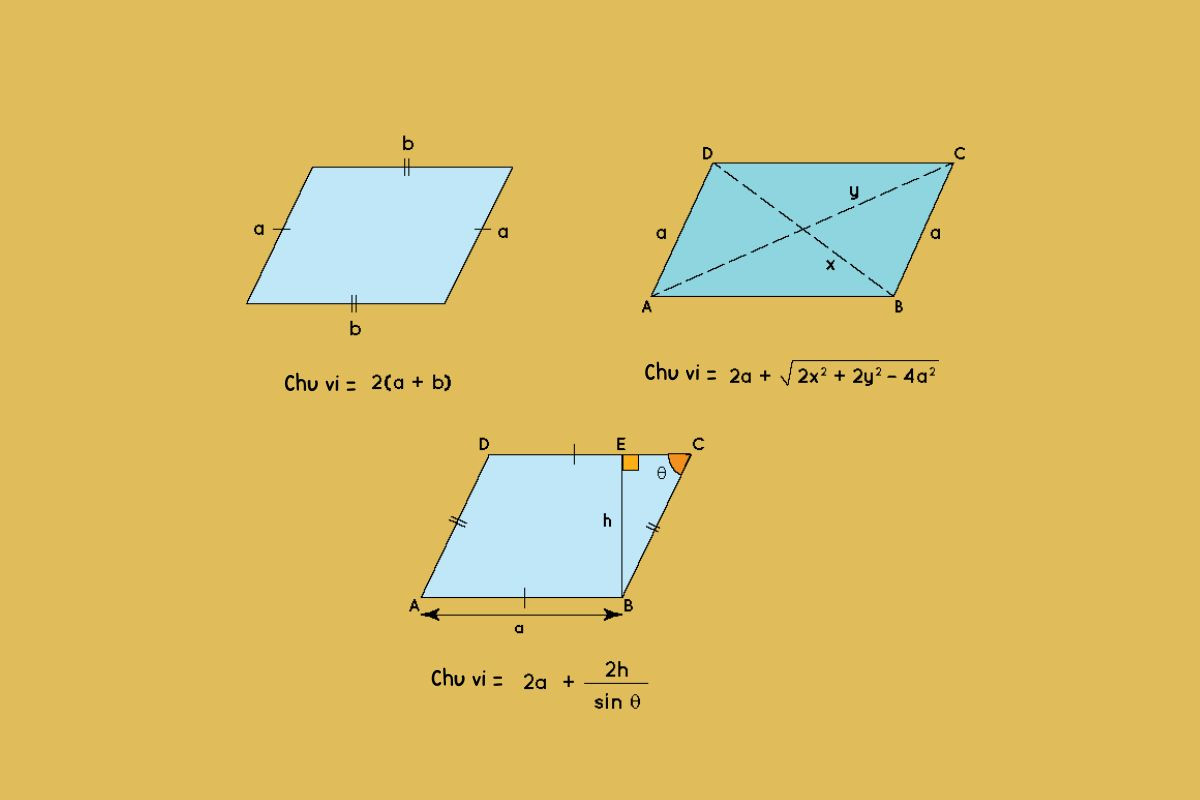
Tính chu vi hình bình hành biết một cạnh và các đường chéo
Công thức:
P = 2a + √(2x 2 + 2y 2 - 4a 2 )
Trong đó a là cạnh a của hình bình hành và x, y là các đường chéo của nó.
Giải thích công thức:
Một hình bình hành có các cạnh a và b và các đường chéo x và y. Giả sử rằng các giá trị của cạnh a và các đường chéo x và y đã cho nhưng giá trị của b không được cho và bài toán yêu cầu tìm chu vi của hình bình hành.
Áp dụng định lý cosin vào tam giác ABD:
x 2 = a 2 + b 2 - 2ab cosBAD
Áp dụng quy tắc cosin cho tam giác ADC:
y 2 = a 2 + b 2 - 2ab cos ADC
Cộng hai phương trình trên:
x 2 + y 2 = 2a 2 + 2b 2 - 2ab (cos BAD + cos ADC) .... (1)
Chúng ta biết rằng hai góc kề bù của một hình bình hành (đó là tính chất của hình bình hành) đều bổ sung cho nhau. Vì thế:
∠BAD + ∠ADC = 180°
∠BAD = 180° - ADC
Áp dụng cos cho cả hai vế:
cos BAD = cos (180° - ADC) = - cos ADC
Thay thế điều này vào (1):
x 2 + y 2 = 2a 2 + 2b 2 - 2ab ( - cos ADC + cos ADC)
x 2 + y 2 = 2a 2 + 2b 2 - 2ab (0)
x 2 + y 2 = 2a 2 + 2b 2
Ta đã có mối liên hệ giữa các cạnh và đường chéo của hình bình hành. Bây giờ, chúng ta sẽ giải nó cho b vì chúng ta không biết độ dài của b.
2b 2 = x 2 + y 2 - 2a 2
b 2 = (x 2 + y 2 - 2a 2 ) / 2
b = √ [(x 2 + y 2 - 2a 2 ) / 2]
Khi đã biết các cạnh của hình bình hành (a và b), chúng ta có thể sử dụng công thức ở phần trước nếu muốn tính chu vi hình bình hành (P).
P = 2a + 2b
P = 2a + 2 √ [(x 2 + y 2 - 2a 2 ) / 2]
P = 2a + √[2(x 2 + y 2 - 2a 2 )
P = 2a + √(2x 2 + 2y 2 - 4a 2 )
Tính chu vi hình bình hành có đáy, chiều cao và góc
Công thức:
P = 2a + 2h / sinθ
Trong đó a là cạnh của hình bình hành, h là chiều cao và θ là góc của hình bình hành.
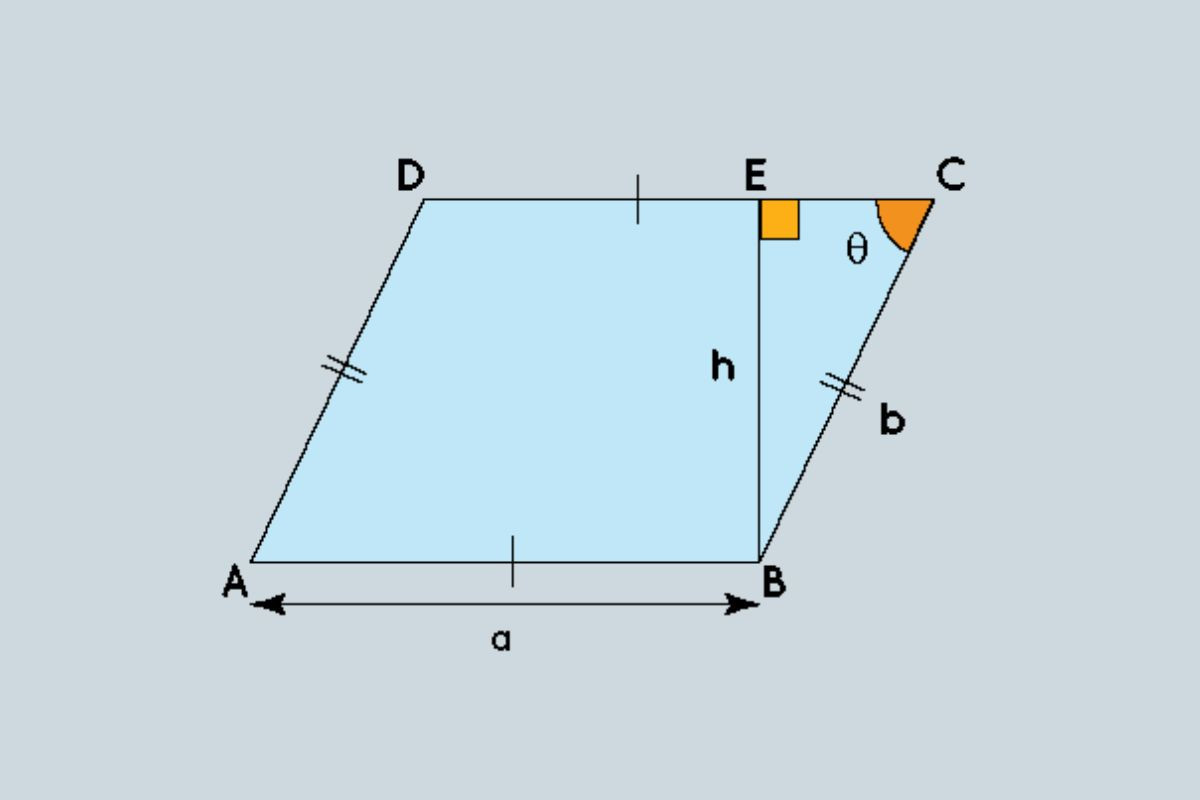
Giải thích công thức:
Chúng ta hãy xem xét một hình bình hành có một cạnh là a, chiều cao tương ứng của nó là h và một trong các góc ở đỉnh là θ. Giả sử cạnh chưa biết của hình bình hành là b. Đầu tiên chúng ta cần tìm b và sau đó tính chu vi.
Áp dụng sin cho tam giác BEC:
Sin θ = h/b
b = h / sin θ
Do đó, chu vi (P) của hình bình hành là:
P = 2a + 2b
P = 2a + 2h / sinθ
Ở đây θ không cần phải là một góc cụ thể của hình bình hành. Nó có thể là góc ở đỉnh bất kỳ vì hai góc liền kề bất kỳ của hình bình hành đều phụ nhau và sin θ = sin (180° - θ), với mọi θ.
Mối liên hệ giữa diện tích và chu vi của hình bình hành
Chúng ta biết rằng diện tích của hình bình hành bằng tích của đáy và chiều cao.
S = b*h (1)
Mối quan hệ giữa diện tích và chu vi của hình bình hành là:
P = 2 (a+b) (2)
Do đó, giá trị của b theo P là:
P/2 = a + b
b=(P/2) – a
Bây giờ, thay thế giá trị của b vào (1):
S = ((P/2) – a)h
Bài tập ứng dụng
Tính chu vi hình bình hành có độ dài đáy và cạnh lần lượt là 10cm và 5cm.
Giải:
Được cho:
Độ dài đáy của hình bình hành = 10 cm
Độ dài cạnh của hình bình hành = 5 cm
Chúng ta biết rằng chu vi của hình bình hành, P = 2(a+b) đơn vị.
Thay thế các giá trị
P = 2(10+5)
P = 2(15)
P = 30cm
Do đó, chu vi của hình bình hành là 30 cm.
Tìm chu vi hình bình hành có cạnh = 14m, đáy = 10m.
Giải:
Chu vi của bình hành động được lựa chọn bởi:
2(a + b)
Trong đó a và b là hai bờ viền nhau
Chu vi = 2 (14 + 10)
Chu vi = 2 (24)
Chu vi = 48m
Tính chu vi của hình bình hành có đáy là 5cm, cạnh dài là 6cm.
Giải:
Chu vi của bình hành động được lựa chọn bởi:
2(a + b)
Trong đó a là đáy và b viền của nó
Chu vi = 2 (5 + 6)
Chu vi = 2 (11)
Chu vi = 22cm
Chu vi của hình bình hành là bao nhiêu khi một cạnh của nó là 15 cm, chiều cao tương ứng là 20 cm và một trong các góc ở đỉnh là 30 độ?
Giải:
Một cạnh của hình bình hành đã cho là a = 15 cm.
Chiều cao của nó là h = 20 cm.
Một góc ở đỉnh là θ = 30°.
Chu vi của nó (P) là
P = 2a + 2h / sinθ
P = 2(15) + (2 × 20) / (sin 30°) = 110 cm
Trả lời: Chu vi hình bình hành đã cho là 110m.
Chu vi của hình bình hành có cạnh dài 8 cm và đường chéo 10 cm và 12 cm là bao nhiêu? Làm tròn câu trả lời của bạn đến hai số thập phân.
Giải:
Một cạnh của hình bình hành đã cho là a = 8 dm.
Đặt cạnh bên kia là b cm.
Đường chéo của nó là x = 10 cm và y = 12 cm.
Sử dụng chu vi của công thức hình bình hành sử dụng một cạnh và các đường chéo, chu vi (P) là
P = 2a + √(2x 2 + 2y 2 - 4a 2 )
P = 2(8) + √(2(10) 2 + 2(12) 2 - 4(8) 2 ) ≈ 31,23 cm
Trả lời: Chu vi của hình bình hành đã cho = 31,23 cm.

Chu vi của hình bình hành là bao nhiêu khi chiều cao là 20cm, góc ở đỉnh là 45° và một cạnh là 12cm?
Giải:
Chu vi của bình hành động được lựa chọn bởi:
P = 2a + 2h/sinθ
P = 2 × 12 + 2 × 20/sin45
P = 24 + 40 × 2
P = 24 + 80
P = 104 cm
Chu vi hình bình hành là 100cm, một cạnh của hình bình hành là 32cm. Tìm độ dài cạnh bên.
Giải thích :
Chu vi của bình hành động được lựa chọn bởi:
P = 2(a + b)
Với a và b là hai bờ viền của nó.
Cho: P = 100cm, a = 32cm
100 = 2 (32 + b)
50 = 32 + b
b = 18cm
Độ dài cạnh của hình bình hành là 18cm.
Chu vi của hình bình hành là 48 cm và một cạnh của nó là 16 cm. Tìm độ dài cạnh bên kia.
Giải:
Cho: Chu vi (P) = 48 cm, và cạnh a = 16 cm. Để tìm độ dài cạnh b còn lại của hình bình hành, chúng ta sẽ sử dụng công thức tính chu vi hình bình hành P = 2(a + b).
P = 2(a + b)
⇒ 48 = 2 (16 + b)
⇒ 16 + b = 48/2
⇒ b = 24 - 16
⇒ b = 8 cm
Trả lời: Cạnh kia của hình bình hành là 8 cm.
Câu hỏi liên quan
Tại sao hai đường chéo của hình bình hành lại cắt nhau tại trung điểm của mỗi đường?
Đây là một trong những tính chất đặc biệt của hình bình hành. Hai đường chéo của hình bình hành chia đôi hình bình hành thành hai tam giác đối xứng nhau qua một đường thẳng.
Hình bình hành nào có chu vi nhỏ nhất?
Hình bình hành có chu vi nhỏ nhất là hình vuông. Lý do là vì hình vuông có tất cả các cạnh bằng nhau và chu vi của hình bình hành được tính bằng tổng độ dài các cạnh. Do đó, hình vuông có chu vi nhỏ nhất so với các hình bình hành khác có cùng diện tích.
Trong thực tế, hình bình hành được ứng dụng như thế nào?
Hình bình hành được ứng dụng trong nhiều lĩnh vực của đời sống, ví dụ như:
- Kiến trúc: Hình bình hành được sử dụng để tạo ra các mái nhà, cửa sổ, sàn nhà và các chi tiết trang trí khác.
- Kỹ thuật: Hình bình hành được sử dụng trong các cấu trúc kim loại như khung xe, cầu và tòa nhà.
- Nghệ thuật: Hình bình hành được sử dụng trong các tác phẩm nghệ thuật như tranh vẽ, thêu thùa và đồ thủ công mỹ nghệ.
- Thời trang: Hình bình hành được sử dụng trong các thiết kế quần áo, giày dép và phụ kiện.
Trên đây là tổng hợp các cách tính chu vi hình bình hành đầy đủ và chi tiết. Bên cạnh việc học thuộc các công thức, tính chất, người học cần kết hợp với làm bài tập thực hành, vận dụng linh hoạt cho từng trường hợp để tìm ra đáp án nhanh nhất.



























