Hình lập phương là gì?
Hình lập phương - một khối đa diện đều ba chiều với 6 mặt đều là hình vuông, 12 cạnh bằng nhau, 8 đỉnh và cứ 3 cạnh gặp nhau tại 1 đỉnh, có 4 đường chéo cắt nhau tại một điểm. Để làm được bài tập thể tích hình lập phương và các dạng nâng cao hơn bạn cần nắm được lý thuyết về hình này.
Công thức tính thể tích hình lập phương
Thể tích hình lập phương là số đo cho không gian chứa bên trong khối lập phương ấy. Nó thể hiện cho lượng chất liệu, vật liệu có thể nhồi vào khối lập phương đó mà không làm thay đổi hình dạng của nó.
Công thức tính thể tích hình lập phương V = a^3
Trong đó:
- V là thể tích hình lập phương (đơn vị: mét khối, cm khối,...)
- a là độ dài cạnh của hình lập phương (đơn vị: mét, cm,...)
Ví dụ 1: Một khối lập phương có cạnh dài 5 cm. Thể tích của khối lập phương đó là: V = 5^3 = 125 cm3.
Ví dụ 2: Một bể nước hình lập phương có cạnh dài 1 mét. Thể tích của bể nước đó là: V = 1^3 = 1 m3.
Bài tập ứng dụng tính thể tích hình lập phương
Để thành thạo công thức và tư duy giải các bài toán liên quan đến thể tích hình lập phương, hãy tham khảo các dạng bài sau:
Tính thể tích hình lập phương khi đã biết độ dài
Cách giải:
- Phân tích đề bài: Xác định độ dài cạnh (a) của hình lập phương được cho trong đề bài.
- Thay giá trị vào công thức: Thay giá trị a đã tìm được vào công thức V = a x a x a để tính thể tích (V).
Ví dụ: Cho hình lập phương, chiều dài các cạnh có số đo là 5 m. Hãy tính thể tích của hình lập phương này.
Lời giải:
Thay số liệu vào công thức V = a x a x a = 5 x 5 x 5 = 75 m³
Vậy thể tích của hình lập phương là 75 cm³
Tính thể tích hình lập phương khi biết Sxq hoặc Stp
Nếu đề bài cho biết diện tích xung quanh Sxq hoặc Stp, ta sẽ tính độ dài cạnh (a) trước, sau đó tính thể tích (V).
Ta có: Sxq = 4 x a x a => Suy ra: a = √(Sxq / 4) và Stq = 6 x a x a => a = √(Stq / 6)
Ví dụ: Cho một hình lập phương có diện tích xung quanh = 16 m2. Hãy tính thể tích của hình lập phương này.
Lời giải: Diện tích xung quanh là 16 m2 => Sxq = 16 = 4 x a x a => 4 = a x a => a = 2 m. Độ dài các cạnh hình lập phương này = 2 m.
Vậy thể tích của hình lập phương là: V = a x a x a = 8 m³
Tính cạnh khi biết thể tích hình lập phương
Tương tự như dạng 2, bạn cần xuất phát từ công thức gốc tính thể tính sau đó tính ra độ dài cạnh.
Ví dụ: Cho hình lập phương có thể tích V = 64 cm³. Hãy tính độ dài cạnh hình lập phương này.
Lời giải: Độ dài cạnh của hình lập phương là: V = a x a x a = 64 => a = 4 cm (theo máy tính online casio fx-580vn)
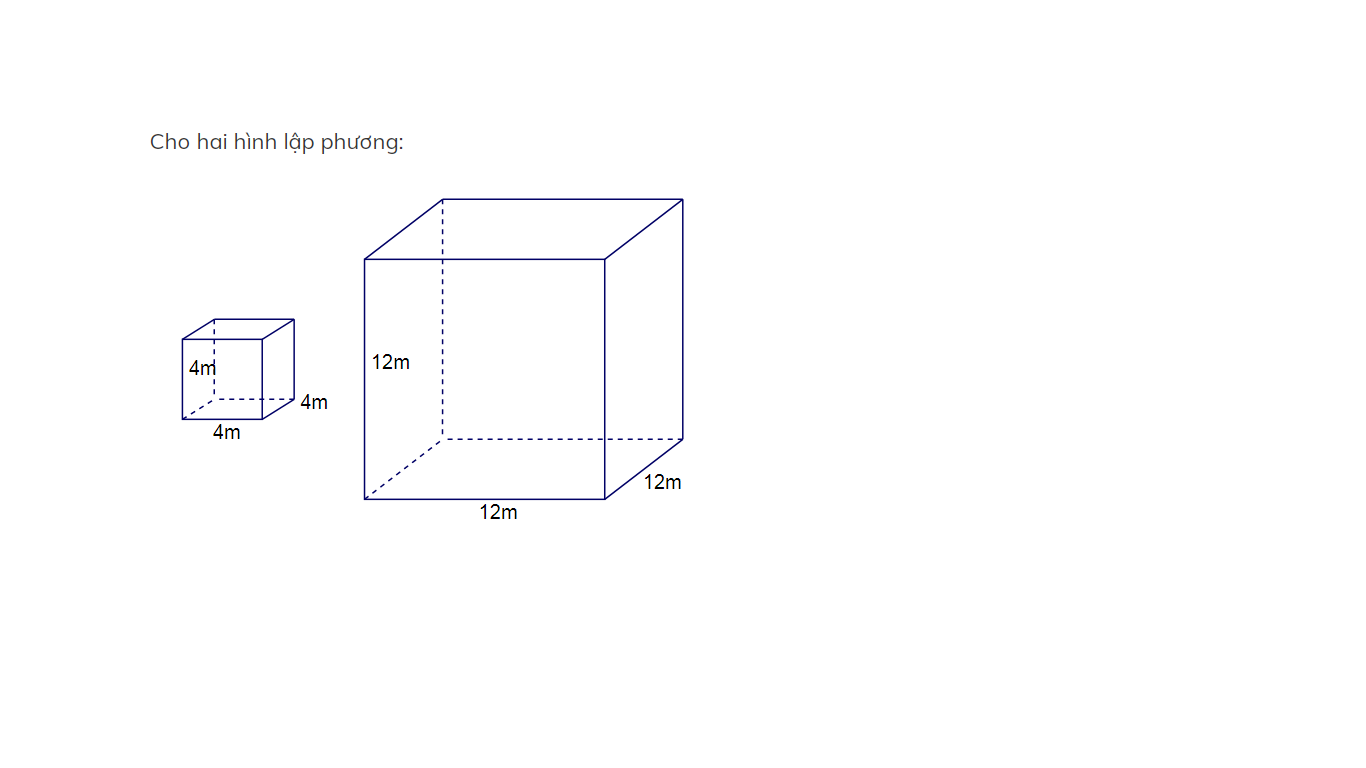
So sánh thể tích của 2 hình lập phương
Ở dạng bài này có 2 cách để chúng ta giải toán:
Cách 1: Áp dụng công thức thông thường tính ra V từng bình rồi so sánh.
Cách 2: Do cùng công thức với nhau và trong công thức chỉ cần so sánh độ dài cạnh của hình lập phương.
- Trường hợp 1: Nếu a1 > a2, thì V1 > V2.
- Trường hợp 2: Nếu a1 < a2, thì V1 < V2.
- Trường hợp 3: Nếu a1 = a2, thì V1 = V2.
Tính thể tích khối cầu nội tiếp hình lập phương
Khối cầu nội tiếp hình lập phương có tâm là tâm của hình lập phương và bán kính bằng 1/2 cạnh của hình lập phương. Để tính thể tích khối cầu, ta cần biết bán kính của nó.
Thể tích khối cầu: V_c = (4/3)πr^3
Trong đó: r là bán kính khối cầu và r bằng 1 nửa cạnh của hình lập phương.
Bài toán về thể tích hình lập phương từ cơ bản đến nâng cao
Bài 1: Một khối lập phương có cạnh dài 4 cm. Tìm thể tích hình lập phương đó.
Lời giải:
Thể tích của khối lập phương đó là: V = a^3 = 4 ^ 3 = 64 cm3
Bài 2: Một bể nước hình lập phương có cạnh dài 1,5 mét. Bể chứa đầy nước. Người ta lấy ra 1/4 lượng nước trong bể. Hỏi lượng nước còn lại trong bể là bao nhiêu mét khối?
Lời giải:
Thể tích của bể nước là:
V = a^3 = 1,5 ^ 3 = 3,375 m3
Lượng nước lấy ra là:
V1 = 1/4 * V = 1/4 * 3,375 m^3 = 0,84375 m3
Lượng nước còn lại trong bể là:
V2 = V - V1 = 3,375 m^3 - 0,84375 m^3 = 2,53125 m3
Bài 3: Một khối rubik có dạng hình lập phương với cạnh dài 3 cm. Mỗi ô nhỏ trên rubik có thể tích là 1 cm³. Hỏi cả khối rubik có bao nhiêu ô nhỏ?
Lời giải:
Thể tích của một khối rubik là: V = a^3 = 3 cm ^ 3 = 27 cm3
Số ô nhỏ trên rubik là:
N = V / V_o = 27/ 1 = 27 ô

Bài 4: Một bể cá hình lập phương có cạnh dài 60 cm. Mực nước trong bể cao 40 cm. Người ta thả một hòn đá vào bể, mực nước dâng lên 50 cm. Hỏi thể tích của hòn đá nói trên là bao nhiêu?
Lời giải:
Thể tích nước trong bể trước khi thả hòn đá là:
V_nước1 = a1^3 = 40 ^ 3 = 64000 cm3
Thể tích nước trong bể sau khi thả hòn đá là:
V_nước2 = a2^3 = 50 cm ^ 3 = 125000 cm^3
Thể tích của hòn đá là:
V_đá = V_nước2 - V_nước1 = 125000 - 64000 = 61000 cm3
Bài 5: Một khối kim loại hình lập phương có cạnh dài 5 cm. Khối kim loại đó nặng 1 kg. Mỗi đề-xi-mét khối kim loại nặng 15 kg. Hỏi khối kim loại đó rỗng hay đặc?
Lời giải:
Dựa vào công thức thể tích hình lập phương, thể tích của khối kim loại là:
V = a^3 = 5 cm ^ 3 = 125 cm^3 = 0,00125 m3
Khối lượng của 1 mét khối kim loại là:
M = 15 * 1000 = 15000 kg/m3
Khối lượng lý tưởng của khối kim loại là:
M1 = V * M = 0,00125 m^3 * 15000 kg/m^3 = 18,75 kg
Vì khối lượng thực tế của khối kim loại (1 kg) nhỏ hơn khối lượng lý tưởng (18,75 kg), nên khối kim loại đó rỗng.
Bài 6: Một khối gỗ hình lập phương có cạnh dài a cm. Người ta cắt đi 8 đỉnh của khối gỗ theo các đường thẳng vuông góc với nhau, tạo thành một khối lập phương mới có cạnh ngắn hơn a - 2 cm. Vậy tính thể tích của khối gỗ mới bằng bao nhiêu?
Lời giải:
Cạnh của khối gỗ mới là: a - 2 cm
Thể tích của khối gỗ mới là:
V' = (a - 2 cm)^3 = a^3 - 6a^2 + 12a - 8
Thể tích của khối gỗ đã mất đi là: V - V' = a^3 - (a^3 - 6a^2 + 12a - 8) = 6a^2 - 12a + 8

Một số bài tự luyện thêm về thể tích hình lập phương:
Bài 1: Một khối kim loại hình lập phương có cạnh dài 2 cm. Khối kim loại đó nặng 16 gam. Mỗi xăng-ti-mét khối kim loại có khối lượng 2 gam. Hỏi khối kim loại đó rỗng hay đặc?
Bài 2: Một bể cá hình lập phương có cạnh dài 30 cm. Người ta đổ nước vào bể sao cho mực nước trong bể cao 2/3 chiều cao của bể. Hỏi trong bể còn chỗ trống để chứa thêm bao nhiêu lít nước? (1 lít = 1 dm³)
Bài 3: Một khối gỗ hình lập phương có cạnh dài 5 cm. Người ta sơn kín tất cả các mặt của khối gỗ này. Tính diện tích toàn phần cần sơn.
Bài 4: Một hình hộp chữ nhật có chiều dài = 8 cm, chiều rộng = 6 cm, chiều cao = 5 cm. Thể tích hình lập phương bằng thể tích của hình hộp chữ nhật đó. Cạnh của hình lập phương đó là bao nhiêu?
Bài 5: Một khối sắt hình lập phương có cạnh dài a cm. Người ta cắt đi 8 đỉnh của khối này theo các đường thẳng vuông góc với nhau, tạo thành một khối lập phương mới có cạnh ngắn hơn a - 2 cm. Tính tỉ số thể tích giữa khối sắt mới và khối ban đầu.
Bài 6: Trong một căn phòng hình lập phương, người ta treo 8 bức tranh hình vuông có cạnh dài 20 cm lên các mặt tường. Tổng diện tích của các bức tranh là bao nhiêu?
Bài 7: Một khối rubik hình lập phương có cạnh dài 3 cm. Mỗi ô vuông nhỏ trên mỗi mặt của rubik có diện tích 1 cm². Khi xáo trộn rubik, có bao nhiêu ô vuông nhỏ đổi vị trí?
Bài 8: Một bể nước hình lập phương có cạnh dài 1,2 mét. Bể chứa đầy nước. Người ta thả một khối gỗ hình lập phương có cạnh dài 0,5 mét vào bể. Mực nước trong bể dâng thêm bao nhiêu?
Bài 9: Một khối bê tông hình lập phương có cạnh dài 4 dm. Khối bê tông đó nặng 1024 kg. Mỗi mét khối bê tông có khối lượng 2500 kg. Hỏi khối bê tông đó rỗng hay đặc?
Bài 10: Một ngôi nhà hình lập phương có cạnh dài 10 mét. Người ta muốn sơn tất cả các mặt ngoài của ngôi nhà, trừ cửa sổ và cửa ra vào. Biết rằng diện tích cửa sổ và cửa ra vào chiếm 20% diện tích một mặt của ngôi nhà. Tính diện tích cần sơn.
Điều gì sẽ xảy ra nếu Trái Đất là một khối lập phương?
Nếu Trái Đất là một khối lập phương thay vì hình cầu, nhiều khía cạnh của hành tinh chúng ta sẽ thay đổi hoàn toàn, dẫn đến những hậu quả to lớn cho mọi dạng sống trên Trái Đất. Lực hấp dẫn sẽ không đồng đều trên toàn bộ bề mặt. Nó sẽ mạnh nhất ở các góc của khối lập phương và yếu nhất ở tâm. Điều này sẽ khiến cho việc di chuyển trên Trái Đất trở nên khó khăn, đặc biệt là leo dốc. Nước sẽ tập trung ở các vùng thấp hơn, tạo thành những đại dương khổng lồ ở tâm mỗi mặt của khối lập phương. Các lục địa sẽ hình thành như những dải đất cao chót vót dọc theo các cạnh của khối lập phương.
Bên cạnh đó, do sự phân bố lực hấp dẫn không đều, khí quyển sẽ mỏng hơn ở các góc và dày hơn ở tâm. Điều này sẽ dẫn đến sự chênh lệch nhiệt độ lớn giữa các khu vực, với các góc lạnh hơn nhiều so với tâm. Ánh sáng mặt trời cũng sẽ phân bố không đều, với các khu vực gần tâm nhận được nhiều ánh sáng hơn các khu vực xa tâm.
Cũng có nhiều chuyên gia sinh vật học cho rằng, sự phân bố sinh vật cũng sẽ không đồng đều, với các khu vực gần tâm có thể hỗ trợ nhiều dạng sống hơn các khu vực xa tâm.

Như vậy, việc học sinh linh hoạt trong cách giải các bài toán về thể tích hình lập phương lớp 5 là vô cùng quan trọng. Nó giúp các bạn phát triển tư duy logic, sáng tạo và khả năng giải quyết vấn đề một cách hiệu quả.
