Số thực là gì?
Trong toán học có rất nhiều loại số khác nhau, trong đó nhiều người thắc mắc không biết số thực là gì. Số thực là một khái niệm cơ bản trong toán học, bao gồm cả số hữu tỉ và số vô tỉ. Số hữu tỉ là những số có thể biểu diễn dưới dạng phân số, trong đó tử số và mẫu số đều là các số nguyên, ví dụ như 1/2, -3/4, hay 5. Số vô tỉ là những số không thể biểu diễn dưới dạng phân số, ví dụ như số pi (π), số e hay căn bậc hai của 2.

Số thực bao gồm tất cả các số nguyên, số thập phân hữu hạn, số thập phân vô hạn tuần hoàn và số thập phân vô hạn không tuần hoàn. Tập hợp các số thực được biểu diễn trên trục số thực, bao phủ toàn bộ các điểm từ âm vô cùng đến dương vô cùng.
Số thực có vai trò quan trọng trong toán học và các lĩnh vực khoa học khác vì chúng cho phép biểu diễn và xử lý một phạm vi rộng lớn các giá trị số học và đo lường liên tục.
Kiểu số thực là gì?
Ngoài tìm hiểu số thực là gì, kiểu số thực là gì cũng là thông tin được nhiều người quan tâm. Kiểu số thực là khái niệm trong lập trình và khoa học máy tính dùng để biểu diễn các số có phần thập phân. Kiểu số thực cho phép lưu trữ và thao tác với các số mà không phải là số nguyên, bao gồm cả các số có phần thập phân và các số vô tỉ.
Tham số thực là gì?
Tham số thực cũng là khái niệm liên quan khi tìm hiểu số thực là gì. Theo quy ước toán học, tham số thực là khái niệm thường được dùng trong giải tích và các phương trình toán học, đề cập đến các giá trị thực có thể được gán cho biến số trong một hàm hoặc phương trình. Các giá trị này là số thực, bao gồm tất cả các số hữu tỉ và vô tỉ trên trục số thực.
Trục số thực là gì?
Trục số thực là một đường thẳng vô hạn được sử dụng để biểu diễn tất cả các số thực. Mỗi điểm trên trục số thực tương ứng với một số thực duy nhất. Ngược lại, mỗi số thực được biểu diễn bởi một điểm duy nhất trên trục này. Trục số thực là công cụ cơ bản trong toán học để trực quan hóa và làm việc với các số thực.
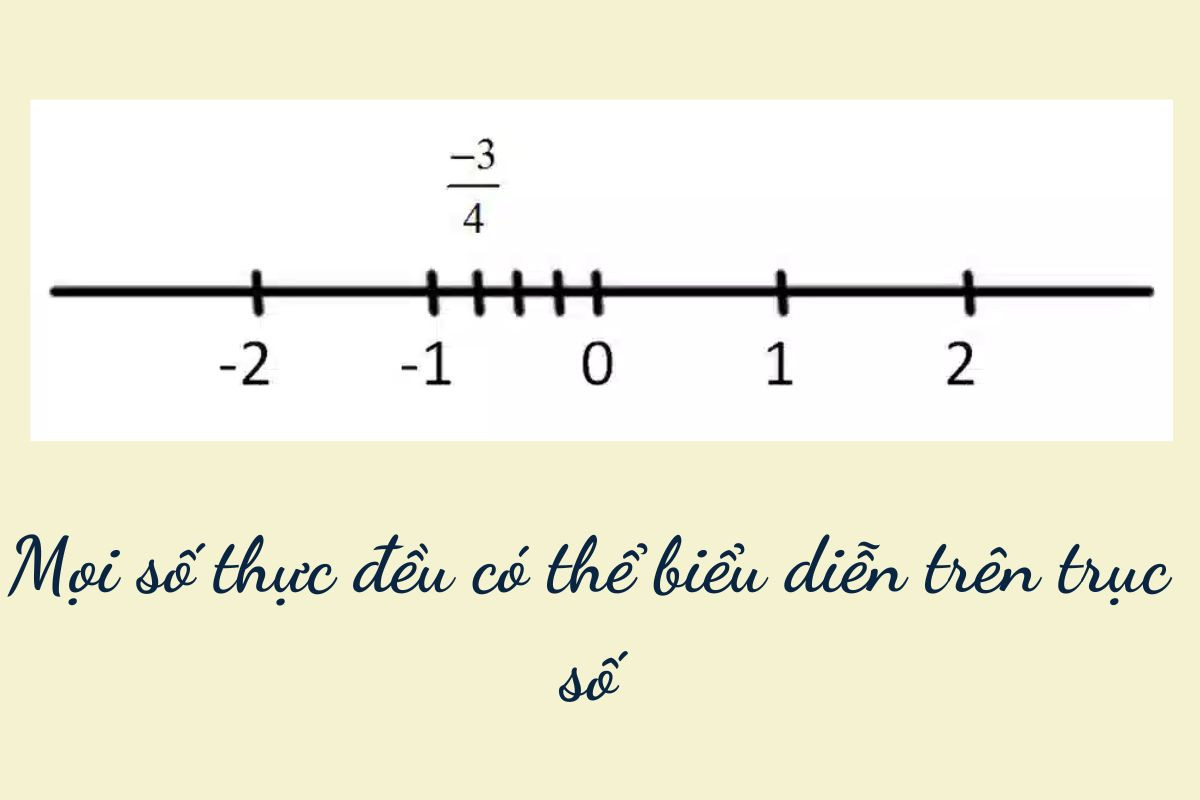
Số thực có phải số phức không?
Sau khi tìm hiểu số thực là gì, nhiều người thường thắc mắc không biết số thực có phải là số phức không. Thực tế số thực và số phức là hai loại số khác nhau nhưng có mối quan hệ với nhau. Theo đó số thực là tập hợp con của số phức.

Cụ thể, số thực là những số có thể biểu diễn trên trục số và bao gồm các số dương, số âm, số 0. Còn số phức là những số có dạng a +bi. Trong đó a và b là các số thực, còn i là đơn vị ảo với tính chất i^2 = -1.
Mỗi số thực có thể được coi là một số phức với phần ảo bằng 0. Nghĩa là số thực a có thể được viết dưới dạng a + 0i. Do đó, tập hợp R là tập hợp con của tập hợp số phức C. Bạn có thể áp dụng tính chất này để giải quyết các dạng toán có liên quan.
Tập hợp số thực được ký hiệu là gì?
Ngoài tìm hiểu số thực là gì, bạn cũng cần nắm rõ ký hiệu của số thực trong toán học để nhận diện và áp dụng các tính chất cơ bản. Theo quy ước, tập hợp số thực được ký hiệu là R. Đây là ký hiệu tiêu chuẩn trong toán học để biểu thị toàn bộ tập hợp các số thực, bao gồm tất cả các số hữu tỉ và số vô tỉ.

Số thực có thể biểu diễn mọi giá trị liên tục trên trục số, từ âm vô cùng đến dương vô cùng. Ký hiệu R xuất phát từ từ "real" trong tiếng Anh, nghĩa là "thực", nhằm phân biệt chúng với các số phức, những số bao gồm cả phần thực và phần ảo. Tập hợp R là một trong những nền tảng cơ bản của toán học và được sử dụng rộng rãi trong nhiều lĩnh vực khác nhau như đại số, giải tích, hình học và nhiều ứng dụng thực tiễn khác.
Số thực là những số nào?
Không biết số thực là gì đồng nghĩa với việc bạn cũng sẽ không biết số thực là những số nào. Số thực bao gồm tất cả các số có thể biểu diễn trên trục số thực, từ âm vô cùng đến dương vô cùng. Cụ thể, số thực được chia thành hai loại chính: số hữu tỉ và số vô tỉ. Trong đó:
Số hữu tỉ
Đây là những số có thể biểu diễn dưới dạng phân số với tử số là các số nguyên và mẫu số khác 0. Số hữu tỉ bao gồm:
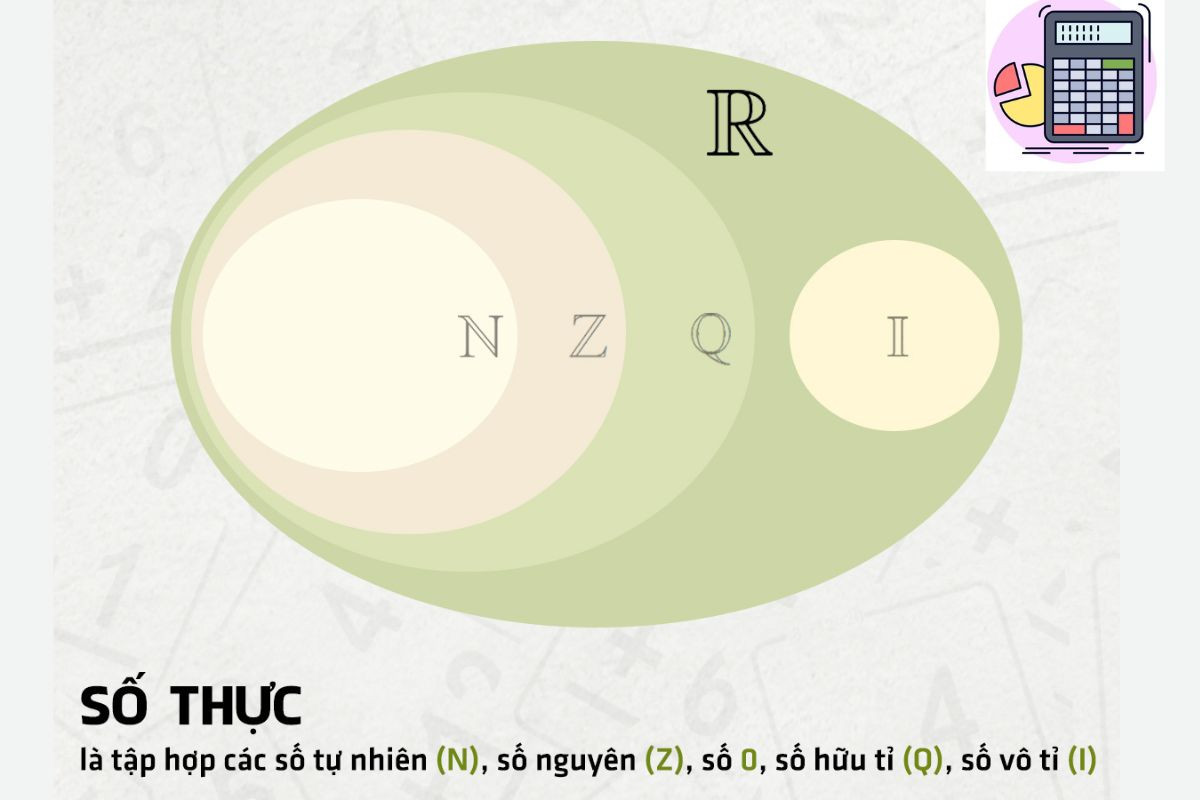
- Số nguyên: Các số nguyên dương, số nguyên âm và số 0. Trong số nguyên bao gồm cả số tự nhiên. Ví dụ: 1, -3, 0, 42
- Phân số: Những số có thể viết dưới dạng phân số. Ví dụ: ½ , ¼
Như vậy: Z ⊂ Q ⊂ R
Số vô tỉ
Số vô tỉ là những số không thể biểu diễn dưới dạng phân số. Phần thập phân của chúng kéo dài vô hạn mà không lặp lại theo chu kỳ. Số vô tỉ bao gồm các số sau:
- Số căn bậc 2 không phải là số hữu tỉ: √2, √3, √5
- Số pi π và số e
Số thực có số 0 không?
Khi đã biết số thực là gì và số thực là những số nào, bạn cũng sẽ biết số thực có số 0 hay không. Số thực bao gồm cả số 0. Trong tập hợp các số thực, số 0 đóng vai trò rất quan trọng. Nó là điểm phân cách giữa các số thực dương và số thực âm trên trục số.
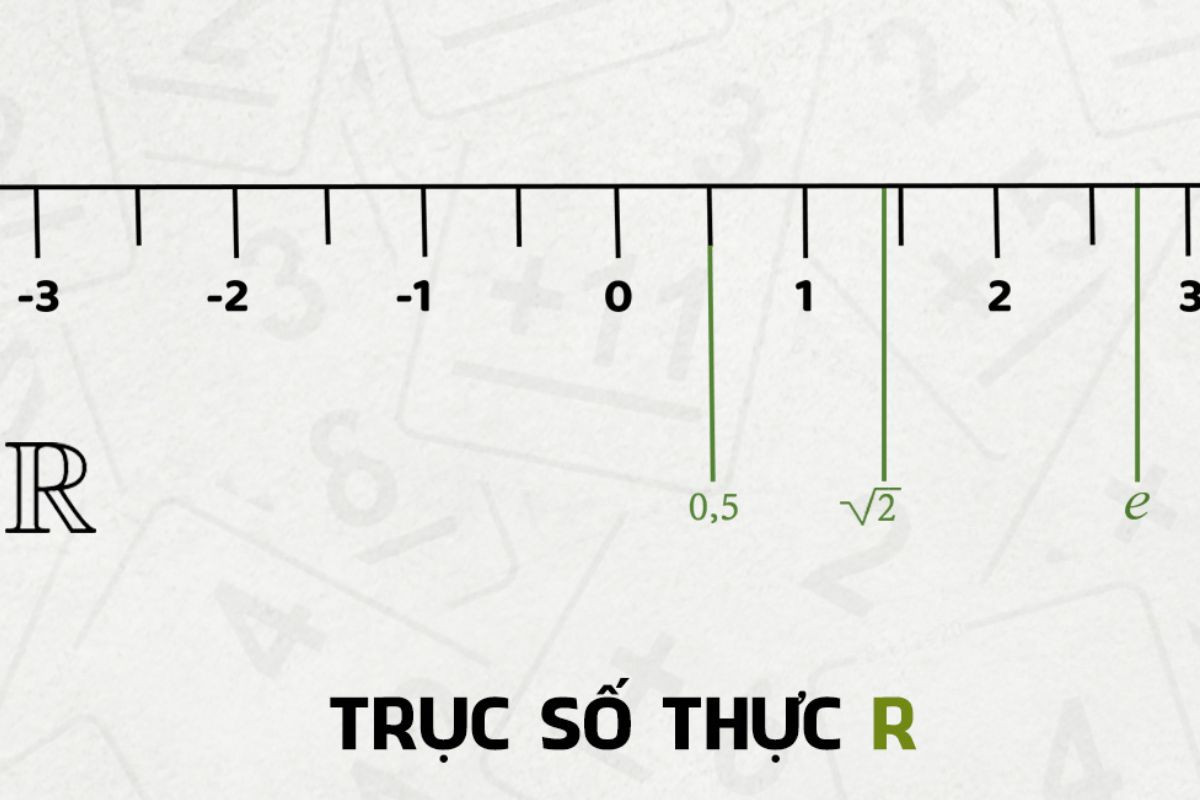
Số 0 là một số nguyên, một số hữu tỉ và cũng là một số thực. Nó thỏa mãn mọi tính chất của số thực, bao gồm tính liên tục và khả năng tham gia vào các phép toán cộng, trừ, nhân và chia (trừ chia cho chính nó). Vì vậy, khi nói đến tập hợp các số thực R, số 0 chắc chắn là một phần của tập hợp này, nằm giữa tất cả các số âm và số dương trên trục số.
Tính chất của số thực trong toán học
Để giải quyết các dạng toán liên quan đến số thực, ngoài việc tìm hiểu số thực là gì, bạn cũng cần nắm rõ những tính chất cơ bản của nó. Dưới đây là các tính chất của số thực:
- Tập hợp số thực là vô hạn và không thể đếm được, nghĩa là giữa hai số thực luôn có vô số số thực khác.
- Với mọi số thực x và số thực dương y, luôn tồn tại số nguyên n sau cho n . y > x.
- Phép cộng, trừ, nhân, chia hai số thực sẽ cho ra kết quả là một số thực.
- Tập hợp số thực là tập hợp đầy đủ, nghĩa là mọi tập hợp con không rỗng của R có giới hạn trên bị chặn đều có cận trên nhỏ nhất.
- Giữa bất kỳ hai số thực nào cũng luôn tồn tại một số thực khác, tạo nên tính liên tục của trục số thực.
Các thuộc tính của số thực
Tìm hiểu số thực là gì và nắm rõ các tính chất, thuộc tính của số thực sẽ giúp bạn dễ dàng giải được các dạng toán có liên quan. Dưới đây là những thuộc tính quan trọng của số thực:
Thuộc tính đại số
Thuộc tính đại số của số thực đề cập đến tính chất giao hoán, tính chất phân phối và tính chất kết hợp. Trong đó, các thuộc tính đại số này đều áp dụng cho phép cộng và phép nhân hai số thực. Cụ thể:
- Giao hoán: a + b = b + a và a . b = b . a
- Kết hợp: (a + b) + c = a + (b + c) và (a . b) . c = a . (b . c)
- Phân phối: a . (b + c) = a . b + a . c
Thuộc tính của số 0 và số 1
Thuộc tính số 0 và số 1 của số thực được quy định như sau:
- Số 0: Là phần tử trung tính của phép cộng, có nghĩa một số thực cộng với 0 cũng bằng chính nó. Ví dụ: a + 0 = a
- Số 1: Là phần tử trung tính của phép nhân vì một số thực nhân với 1 cũng bằng chính nó. Ví dụ: a . 1 = a
Thuộc tính của phép trừ và phép chia
Để thực hiện các phép toán liên quan đến số thực, ngoài tìm hiểu số thực là gì, bạn cũng cần nắm rõ thuộc tính của phép trừ và phép chia hai số thực. Cụ thể:
- Phép trừ: Phép trừ hai số thực là phép cộng với số đối: a - b = a + (-b).
- Phép chia: Phép chia hai số thực là phép nhân với số nghịch đảo: a : b = a . 1/b (với b # 0)
Một số dạng toán về số thực
Số thực là nền tảng trong toán học và nó liên quan đến rất nhiều dạng toán khác nhau. Để giải được các dạng toán liên quan đến số thực, việc nắm rõ số thực là gì và các tính chất của nó là rất quan trọng. Dưới đây là những dạng toán về số thực thường gặp:
Dạng 1: Giải phương trình và bất phương trình:
Đây là dạng toán phổ biến nhất về số thực. Bạn có thể áp dụng tính chất của số thực để giải phương trình bậc nhất, phương trình bậc hai, phương trình chứa dấu giá trị tuyệt đối và bất phương trình. Dưới đây là các ví dụ:
Ví dụ 1: Giải phương trình 2x + 3 = 8
=> 2x = 8 - 3 = 5
=> x = 5 : 2
=> x = 2.5
Ví dụ 2: Giải bất phương trình: -2x + 3 > 8
=> -2x > 8 - 3
=> -2x > 5
=> x < -2.5
Dạng 2: Giải hệ phương trình:
Số thực cũng thường xuyên xuất hiện trong dạng toán giải hệ phương trình, bao gồm hệ phương trình bậc nhất hai ẩn và hệ phương trình phi tuyến. Dưới đây là các ví dụ:
Giải hệ phương trình sau:
{ 3x - 2y = 5
{ 2x + y = 8
Vì ở phương trình thứ hai, hệ số của y là 1 nên ra sẽ rút y theo x để giải hệ phương trình này.
Ta có: 2x + y = 8 ⇔ y = 8 - 2x
Thay y vào phương trình (1), ta được kết quả như sau:
3x - 2(8 - 2x) = 5
⇔ 3x - 16 + 4x = 5
⇔ 7x = 21
⇔ x = 21 : 7 = 3
Với x = 3, thế vào một trong hai phương trình trên, ta có y = 2
Như vậy, nghiệm của hệ phương trình trên là (x;y) = (2;3)
Dạng 3: Tính giá trị biểu thức:
Số thực cũng liên quan đến một số dạng toán tính giá trị biểu thức như biểu thức đại số, biểu thức chứa dấu giá trị tuyệt đối. Dưới đây là các ví dụ:
Tính giá trị biểu thức: 5 + ½ = 10/2 + ½ = 11/2 = 5.5
Ngoài ra còn có rất nhiều dạng toán liên quan đến số thực như phương trình lượng giác, dãy số và chuỗi, bài toán tích phân, bài toán giới hạn và đạo hàm, dạng toán tìm cực trị,... Và tất nhiên để giải được các bài toán này thì bạn cần hiểu đúng số thực là gì và các thuộc tính của nó.
Tìm hiểu số thực là gì và các tính chất của số thực trong toán học giúp bạn dễ dàng áp dụng để giải quyết các dạng toán có liên quan. Hơn nữa, nắm rõ các thuộc tính đại số của số thực cũng giúp bạn tránh được các sai sót khi thực hiện các phép toán cộng, trừ, nhân, chia hai số thực.
