Lý thuyết về hình trụ
Trước khi tìm hiểu công thức diện tích xung quanh hình trụ, hãy hiểu rằng, hình trụ tròn là một hình học không gian cơ bản, được tạo thành bởi các yếu tố sau:
- Mặt trụ: Là một mặt cong được tạo ra bởi đường thẳng di chuyển song song với trục và cách trục một khoảng cố định.
- Hai đáy: Là hai đường tròn bằng nhau và song song với nhau, vuông góc với trục.
- Trục: Là đường thẳng vuông góc với hai đáy và đi qua tâm của hai đáy.
- Chiều cao: Là khoảng cách hai đáy.
Hình trụ tròn có thể được hình thành bằng cách quay một hình chữ nhật quanh một cạnh cố định. Cạnh cố định này sẽ trở thành trục của hình trụ. Hai cạnh còn lại sẽ quét ra hai đường tròn bằng nhau và song song, tạo thành hai đáy của hình trụ. Các cạnh ngắn hơn sẽ tạo thành các đường sinh, là những đường thẳng vuông góc với hai đáy và có độ dài bằng chiều cao của hình trụ.
Ngoài ra, còn có hình trụ nghiêng, được tạo ra bằng cách quay hình chữ nhật quanh một trục không vuông góc với mặt phẳng chứa hình chữ nhật.
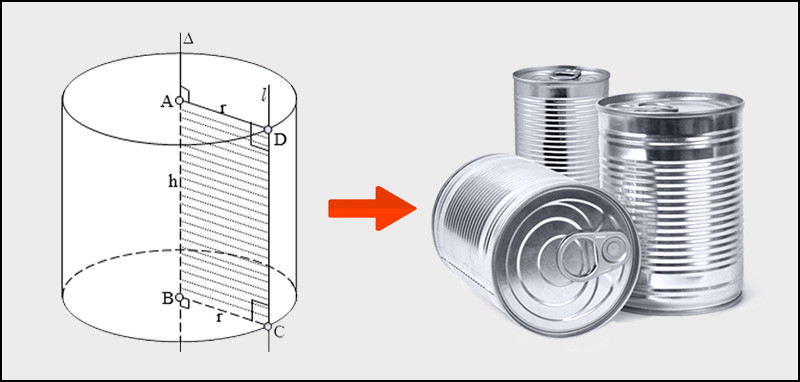
Diện tích xung quanh hình trụ
Diện tích xung quanh hình trụ là diện tích của mặt bao quanh hình trụ, không bao gồm diện tích hai đáy. Nói cách khác, diện tích xung quanh hình trụ là diện tích của một hình chữ nhật có chiều cao bằng chiều cao của hình trụ và chiều rộng bằng chu vi đường tròn đáy.
Công thức tính
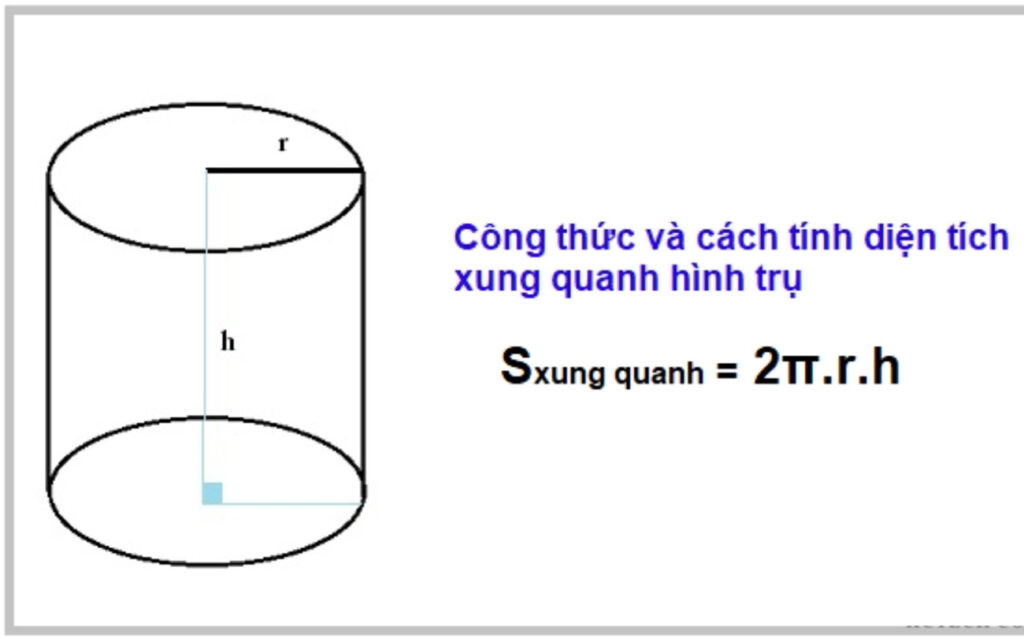
Công thức tính diện tích xung quanh hình trụ: Sxq = 2πrh
Giải thích các ký hiệu:
- Sxq: Diện tích xung quanh hình trụ
- π (pi): Hằng số xấp xỉ 3,14
- r: Bán kính đường tròn đáy hình trụ
- h: Chiều cao hình trụ
Ta chứng minh công thức tính diện tích xung quanh hình trụ bằng phương pháp cắt và ghép:
Cắt hình trụ dọc theo chiều cao vuông góc từ đáy đến đỉnh. Mở phẳng hình trụ sau khi cắt, ta thu được một hình chữ nhật. Chiều dài của hình chữ nhật chính là chu vi đường tròn đáy của hình trụ. Chu vi đường tròn đáy bằng 2πr. Chiều rộng của hình chữ nhật này chính bằng chiều cao của hình trụ (h).
Diện tích xung quanh hình trụ bằng diện tích của hình chữ nhật thu được sau khi cắt và mở phẳng: Sxq = Shcn = 2πr x h.
Ví dụ minh hoạt:
Cho một hình trụ có bán kính đáy r = 3 cm và chiều cao h = 5 cm. Tính diện tích xung quanh (Sxung quanh) của hình trụ này.
Theo công thức và tính bằng máy tính casio fx-580vn plus online:
Sxq = 2πr x h
Sxq = 2π * 3 * 5 = 30π (cm²)
Vậy diện tích xung quanh của hình trụ này là 30π cm².
Bài toán ứng dụng tính diện tích hình trụ trong thực tế
Bài toán 1: Tính diện tích vật liệu làm thùng nước
Đề bài: Một công ty sản xuất thùng nước dạng hình trụ có chiều cao 15 dm và đường kính đáy là 10 dm. Hãy tính diện tích vật liệu cần dùng để làm thùng nước này, không tính nắp đậy.
Hướng dẫn giải:
Bán kính đáy của thùng nước sẽ là: r = 10/2= 5 dm
Diện tích xung quanh của thùng nước (không tính nắp đậy): Sxq = 2 x π x r x h = 2 x π x 5 x 15
Sxq = 471 dm2
Bài toán 2: Tính diện tích giấy cần dùng để bọc pháo hoa
Đề bài: Một công ty sản xuất pháo hoa cần bọc xung quanh cây pháo hoa hình trụ bằng giấy. Cây pháo này có chiều cao là 3 dm và bán kính đáy là 5 dm. Tính diện tích giấy cần dùng để bọc xung quanh cây pháo hoa này.
Hướng dẫn giải:
Diện tích giấy: S = 2 x π x r x h
S = 2 x π x 5 x 30 = 942.48 dm2
Bài toán 3: Tính diện tích vải cần thiết để làm cột trang trí
Đề bài: Cột trang trí sự kiện cần được bọc kín xung quanh bằng vải. Cột mang hình dáng của một hình trụ với chiều cao là 3m và bán kính đáy 0,2 m. Tính diện tích vải đủ để bọc cột trang trí này.
Hướng dẫn giải:
Diện tích vải: S = 2 x π x r x h
S = 2 x π x 0.2 x 3 ≈3.77 m2
Diện tích xung quanh hình lăng trụ
Hình lăng trụ là một đa diện được tạo thành bởi hai mặt đáy là các đa giác bằng nhau và các mặt bên là các hình bình hành.
Đặc điểm:
- Hai mặt đáy của hình lăng trụ là các đa giác tương đẳng, nghĩa là có cùng số cạnh, cùng số đo góc và các cạnh tương ứng bằng nhau.
- Các mặt bên của hình lăng trụ là các hình bình hành, có thể khác nhau hoặc giống nhau.
- Mọi tiết diện song song với hai đáy đều là các đa giác tương đẳng với hai đáy.
Gần giống diện tích xung quanh hình trụ, công thức tính diện tích xung quanh (Sxq) của hình lăng trụ đứng sẽ là:
Sxq = Cđáy* h
Trong đó:
- Cđáy là chu vi đáy
- h là chiều cao của hình lăng trụ
Ví dụ minh hoạ: Coi một hình lăng trụ đứng có đáy là hình vuông cạnh a = 5 cm và chiều cao h = 10 cm. Diện tích xung quanh của hình lăng trụ này được tính như sau:
Chu vi đáy (Cđáy) = 4a = 4 * 5 = 20 cm
Diện tích xung quanh (Sxq) = 20 * 10 = 200 cm²

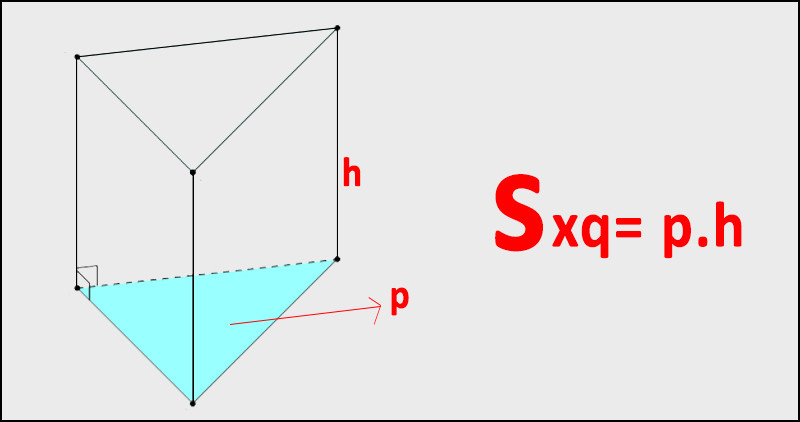
Diện tích xung quanh hình lăng trụ đứng tam giác
Hình lăng trụ đứng tam giác là hình lăng trụ đứng có hai mặt đáy là các tam giác bằng nhau và các mặt bên là các hình chữ nhật.
Công thức tính diện tích xung quanh (Sxq) của hình lăng trụ đứng tam giác:
Sxq = Cđáy x h
Trong đó:
- Cđáy: Chu vi đáy của hình lăng trụ (tổng độ dài ba cạnh của tam giác đáy)
- h: Chiều cao của hình lăng trụ (khoảng cách vuông góc giữa hai mặt đáy)
Ví dụ: Cho một hình lăng trụ đứng tam giác có chiều cao h = 8 cm và cạnh đáy là tam giác đều với độ dài cạnh là a = 6 cm. Tính diện tích xung quanh (Sxq) của hình lăng trụ này.
Giải:
Chu vi đáy (Cđáy) = 3a = 3 * 6 = 18 cm
Diện tích xung quanh (Sxq) = Cđáy * h = 18 * 8 = 144 cm²
Tổng hợp bài tập từ cơ bản đến nâng cao về hình trụ
Dưới đây là một số bài tập từ cơ bản đến nâng cao liên quan đến tính diện tích xung quanh hình trụ cũng như các bài toán thực tế thú vị.
Bài tập có lời giải
Bài 1: Hình trụ có bán kính đáy r = 4 cm và chiều cao h = 6 cm. Hãy tính diện tích xung quanh (Sxq) của hình trụ này.
Giải:
Tính diện tích xung quanh (Sxq) ta áp dụng công thức: Sxq = 2πrh
Thay số: r = 4 cm, h = 6 cm
Kết quả: Sxq = 2π . 4 . 6 ≈ 150,79 cm²
Bài 2: Hình trụ có chiều cao h = 7 cm và diện tích xung quanh (Sxq) bằng 310 cm². Hãy tính diện tích toàn phần (Stp) của hình trụ này.
Giải:
Tính bán kính đáy (r) từ diện tích xung quanh (Sxq = 310 cm²), ta có:
Sxq = 2πrh
Do đó, r = Sxq / (2πh) = 310 cm² / (2π . 7 cm) ≈ 7 cm
Tính diện tích toàn phần (Stp) của hình ta cần áp dụng công thức: Stp = 2πr(r + h)
Thay số: r = 7 cm, h = 7 cm
Kết quả: Stp = 2π . 7 . (7 + 7) ≈ 616 cm²
Bài 3: Một bóng đèn huỳnh quang dài 1,2 m và có đường kính đáy 4 cm. Bóng đèn được đặt khít vào một ống giấy cứng dạng hình hộp chữ nhật. Hãy tính diện tích phần giấy cứng cần dùng để làm vỏ hộp.
Giải:
Tính bán kính đáy (r): r = d / 2 = 4 cm / 2 = 2 cm
Tính diện tích phần giấy cứng:
Diện tích phần giấy cứng chính là diện tích xung quanh của hình hộp chữ nhật có kích thước đáy là 4 cm x 4 cm và chiều cao là 120 cm.
Diện tích xung quanh hình hộp chữ nhật: Sxq = 120 * 4 * 4= 1920 cm²
Bài 4: Mô hình của một cái lọ thí nghiệm dạng hình trụ (không nắp) có bán kính đáy r = 14 cm và chiều cao h = 10 cm. Hãy tính tổng diện tích của mặt xung quanh và một mặt đáy của lọ thí nghiệm này.
Gợi ý giải:
Diện tích xung quanh lọ là: Sxq = 2πrh
Tính diện tích một mặt đáy (Sđáy): Sđáy = πr²
Diện tích xung quanh cộng với diện tích một đáy là: 2πrh + πr² = 496 cm2
Bài 5: Cho một hình trụ có bán kính đáy R và chiều cao h. Nếu tăng chiều cao hình trụ lên hai lần đồng thời giảm bán kính đáy hai lần thì điều gì xảy ra với:
a) Thể tích hình trụ?
b) Diện tích toàn phần hình trụ?
c) Diện tích xung quanh hình trụ?
d) Chu vi đáy hình trụ?
Gợi ý giải:
Giả sử:
- R: Bán kính đáy ban đầu của hình trụ.
- h: Chiều cao ban đầu của hình trụ.
- R': Bán kính đáy mới của hình trụ sau khi thay đổi.
- h': Chiều cao mới của hình trụ sau khi thay đổi.
Do có sự thay đổi nên: h' = 2h và R' = R/2.
Ta sẽ phân tích từng ý:
a) Thể tích hình trụ:
Thể tích hình trụ ban đầu: V = πR²h.
Thể tích hình trụ sau khi thay đổi: V' = πR'²h' hay V' = π(R/2)² . 2h = πR²h/4.
Nhận xét: Thể tích hình trụ giảm đi 4 lần.
b) Diện tích toàn phần hình trụ:
Diện tích toàn phần ban đầu: Stp = 2πR(R + h) = 2πR² + 2πRh
Diện tích toàn phần sau khi thay đổi: Stp' = 2πR'(R' + h').
Thay đổi: Stp' = 2π(R/2)(R/2 + 2h) = 2πR² + πR²h/2.
Nhận xét: Diện tích toàn phần có thay đổi.
c) Diện tích xung quanh hình trụ:
Diện tích xung quanh ban đầu: Sxq = 2πRh.
Diện tích xung quanh sau khi thay đổi: Sxq' = 2πR'h'.
Thay đổi: Sxq' = 2π(R/2) . 2h = 2πRh.
Nhận xét: Diện tích xung quanh không thay đổi.
d) Chu vi đáy hình trụ:
Chu vi đáy ban đầu: C = 2πR.
Chu vi đáy sau khi thay đổi: C' = 2πR'.
Thay đổi: C' = 2π(R/2) = πR.
Nhận xét: Chu vi đáy giảm đi 2 lần.

Một số bài tự luyện
Bài 1: Một hình trụ có bán kính đáy r = 5 cm và chiều cao h = 10 cm. Tính diện tích xung quanh của hình trụ.
Bài 2: Một chiếc hộp đựng nước dạng hình trụ có chiều cao h = 20 cm và đường kính đáy d = 12 cm. Tính diện tích xung quanh của hộp nước.
Bài 3: Một cột trụ hình trụ có bán kính đáy r = 40 cm và chiều cao h = 15 m. Tính diện tích xung quanh của cột trụ.
Bài 4: Một hình trụ có bán kính đáy r là số nguyên dương và chiều cao h = 2r. Chứng minh rằng diện tích toàn phần của hình trụ đó gấp rưỡi diện tích toàn phần của nó.
Bài 5: Một hình trụ có diện tích xung quanh Sxq = 314 cm² và chiều cao h = 5 cm. Tính bán kính đáy r của hình trụ.
Bài 6: Một khối gỗ hình trụ có bán kính đáy r = 3 cm và chiều cao h = 8 cm. Người ta khoét bỏ một khối gỗ hình trụ nhỏ hơn đồng trục với khối trụ ban đầu, có bán kính đáy r' = 2 cm và chiều cao h' = 5 cm. Tính diện tích xung quanh còn lại của khối gỗ.
Bài 7: Một bể bơi hình trụ có đường kính đáy d = 20 m và chiều cao h = 4 m. Để lát gạch toàn bộ mặt ngoài (bao gồm cả đáy) của bể bơi, cần bao nhiêu mét vuông gạch?
Bài 8: Một xưởng sản xuất phuy thép hình trụ có bán kính đáy r = 50 cm và chiều cao h = 120 cm. Để sơn toàn bộ mặt ngoài (bao gồm cả đáy) của một phuy thép, xưởng sản xuất cần bao nhiêu lít sơn (coi 1 lít sơn tương đương với 1 mét vuông diện tích)?
Dạng bài tập liên quan đến diện tích xung quanh hình trụ là một phần quan trọng trong chương trình toán học THCS và THPT. Việc nắm vững các công thức, phương pháp tính toán và luyện tập thường xuyên sẽ giúp học sinh có thể giải được các bài tập một cách chính xác và hiệu quả.
