Giới thiệu về hình tứ giác
Hình tứ giác là một trong những khái niệm cơ bản trong hình học và có ứng dụng rộng rãi trong nhiều lĩnh vực khác nhau. Muốn tính diện tích hình tứ giác không phải là việc đơn giản, do vậy bạn cần hiểu rõ về định nghĩa, tính chất cũng như các đặc điểm của hình đa giác này.
Định nghĩa hình tứ giác
Trong hình học phẳng, tứ giác là một đa giác có bốn góc, bốn đỉnh và bốn cạnh. Các cạnh của tứ giác có thể là các đường thẳng bất kỳ, không cần phải song song hoặc bằng nhau. Tổng 4 góc trong của một tứ giác luôn bằng 360 độ.
Một số đặc điểm chính của hình tứ giác bao gồm:
- Số cạnh và góc: Tứ giác có 4 cạnh và 4 góc.
- Các cạnh: Các cạnh của tứ giác có thể bằng nhau hoặc khác nhau về độ dài.
- Các góc: Các góc của tứ giác có thể bằng nhau hoặc khác nhau về độ lớn.

Các loại hình tứ giác
Tùy theo các đặc điểm của các cạnh và góc, tứ giác có thể được phân thành các loại bao gồm:
- Tứ giác đều - Hình vuông: Cả 4 cạnh và 4 góc của tứ giác đều đều nhau. Tất cả các góc trong đều bằng 90 độ.
- Hình chữ nhật: Có 4 góc vuông (90 độ) và các cạnh đối nhau bằng nhau.
- Hình bình hành: Có 2 cặp cạnh song song và bằng nhau; các góc đối nhau bằng nhau.
- Hình thang: Có 2 cạnh song song nhau và các góc không phải là 90 độ.
- Hình thoi: Có 4 cạnh bằng nhau và các góc đối nhau bằng nhau
- Tứ giác vuông: Tứ giác có ít nhất một góc bằng 90 độ. Đối với loại tứ giác này, đường chéo có thể là đường chéo chính hoặc đường chéo phụ, tùy thuộc vào cách chúng cắt nhau.
- Tứ giác lồi: Các góc của tứ giác lồi đều nhỏ hơn 180 độ. Các đường chéo của tứ giác lồi nằm hoàn toàn bên trong hình.
- Tứ giác lõm: Tứ giác có ít nhất một góc trong lớn hơn 180 độ. Trong tứ giác lõm, một đoạn thẳng nối hai điểm của tứ giác có thể cắt qua tứ giác bên ngoài.
Ngoài ra, còn có các loại tứ giác đặc biệt khác như hình thang cân (hình thang có hai góc kề một đáy bằng nhau) và tứ giác nội tiếp (tứ giác mà bốn đỉnh đều nằm trên một đường tròn).
Công thức tính diện tích hình tứ giác
Bài tập về diện tích hình tứ giác là một trong những dạng rất hay gặp và phổ biến trong toán học. Tùy thuộc vào từng loại tứ giác cụ thể mà cách tính diện tích cũng sẽ khác nhau. Dưới đây là các công thức tính diện tích cơ bản của một số loại tứ giác phổ biến:
- Công thức cho hình chữ nhật: Diện tích = a * b
- Công thức cho hình vuông: Diện tích = a * a
- Công thức cho hình bình hành: Diện tích = a * h
- Công thức cho hình thang: Diện tích = 1/2 * (a + b) * h
- Công thức cho hình thoi: Diện tích = 1/2 * (d1 * d2)
Công thức tính diện tích hình tứ giác không đều bất kỳ
Tính diện tích của một hình tứ giác bất kỳ là một kiến thức cơ bản nhưng vô cùng quan trọng trong hình học. Sau đây là các phương pháp và công thức giúp bạn thực hiện điều này một cách dễ dàng.
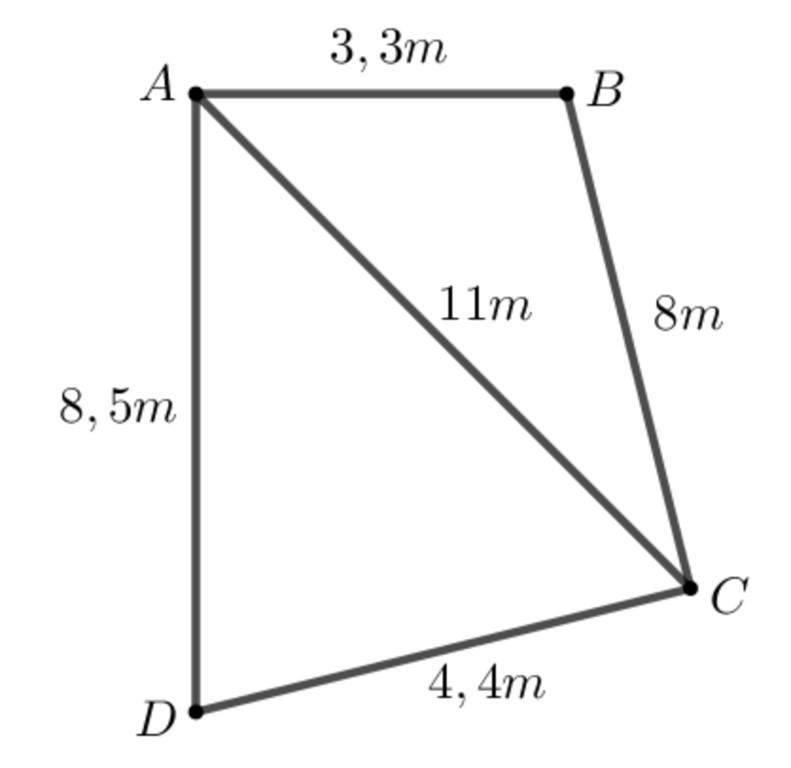
Công thức Heron
Khi tính diện tích của các hình tứ giác không đều, việc tính toán có thể trở nên phức tạp, đặc biệt khi ta không biết được góc giữa các cạnh. Tuy nhiên, công thức Heron cung cấp một giải pháp hiệu quả để giải quyết vấn đề này.
Quy trình tính diện tích hình tứ giác không đều bằng công thức Heron bao gồm các bước sau:
- Vẽ một đường chéo để chia tứ giác thành hai tam giác nhỏ.
- Tính diện tích của mỗi tam giác sử dụng công thức Heron, dựa trên độ dài ba cạnh của tam giác.
- Sau đó cộng diện tích của hai tam giác lại ta được tổng diện tích của tứ giác.
Công thức Heron cho một tam giác với ba cạnh a, b và c là: Diện tích tam giác = √(p(p-a)(p-b)(p-c))
Trong đó p là nửa chu vi của tam giác, tức là (a+b+c)/2.
Bằng cách áp dụng công thức Heron cho từng tam giác được chia từ tứ giác, ta có thể tính được diện tích tổng cộng của tứ giác không đều mà không cần biết các góc của nó.
Lưu ý: Công thức Heron chỉ được áp dụng đối với trường hợp tất cả các điểm của tứ giác cùng nằm trên một mặt phẳng. Đối với các tứ giác đặc biệt như hình vuông hay hình thoi, vẫn có các công thức tính diện tích riêng biệt.

Công thức Brahmagupta
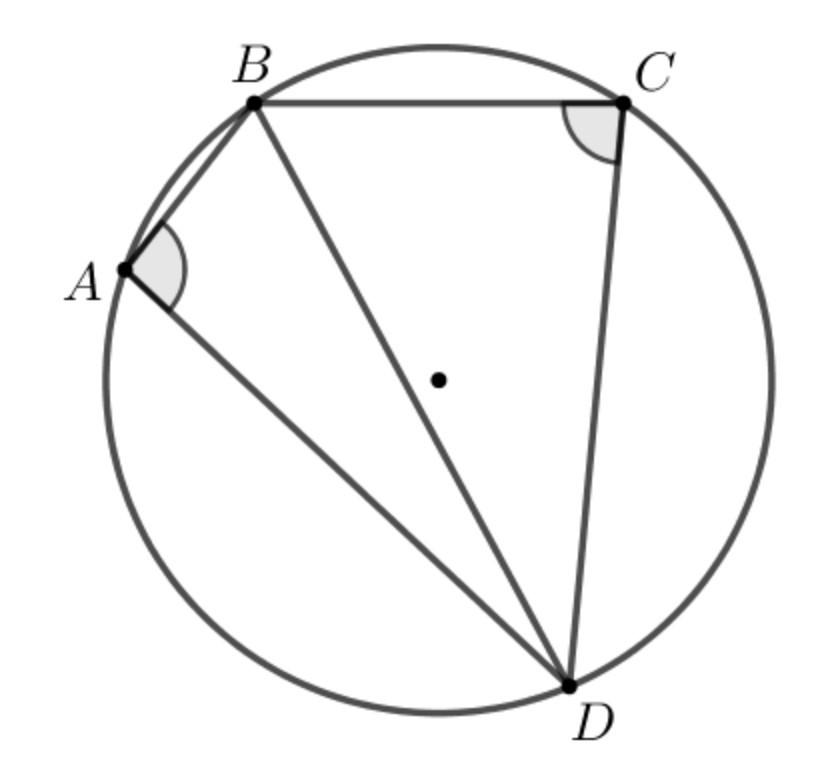
Công thức Brahmagupta là một phương pháp hữu ích để tính diện tích của một tứ giác nội tiếp, tức là tứ giác có các đỉnh nằm trên một đường tròn. Công thức này được đặt theo tên của nhà toán học Ấn Độ Brahmagupta, người đã đề xuất công thức vào thế kỷ 7.
Để sử dụng công thức Brahmagupta, bạn cần biết độ dài các cạnh của tứ giác và tính toán nửa chu vi của nó. Các bước chi tiết bao gồm:
- Xác định độ dài bốn cạnh tứ giác: Gọi độ dài các cạnh của tứ giác nội tiếp lần lượt là a, b, c, d.
- Tính nửa chu vi p = (a + b + c + d)/2.
- Thay các giá trị vừa tính được vào công thức:
- Tính toán và thu được diện tích của tứ giác.
Cách tính diện tích hình tứ giác theo đường chéo và góc tạo bởi hai đường chéo
Để tính diện tích của một tứ giác bằng cách sử dụng độ dài của hai đường chéo và góc tạo bởi chúng, ta có công thức sau:
Diện tích của tứ giác ABCD = 1/2 × d1 × d2 × sin(θ)
Trong đó:
- d1 và d2 là độ dài của hai đường chéo AC và BD
- θ là góc giữa hai đường chéo AC và BD
Cách sử dụng:
- Xác định độ dài hai đường chéo AC (d1) và BD (d2) của tứ giác ABCD.
- Tính góc θ giữa hai đường chéo AC và BD.
- Áp dụng vào công thức: Diện tích = 1/2 × d1 × d2 × sin(θ)
- Tính toán và thu được diện tích của tứ giác bằng công cụ hỗ trợ máy tính fx-580 online.
Cách tính diện tích hình tứ giác khi biết độ dài hai cạnh và góc giữa chúng
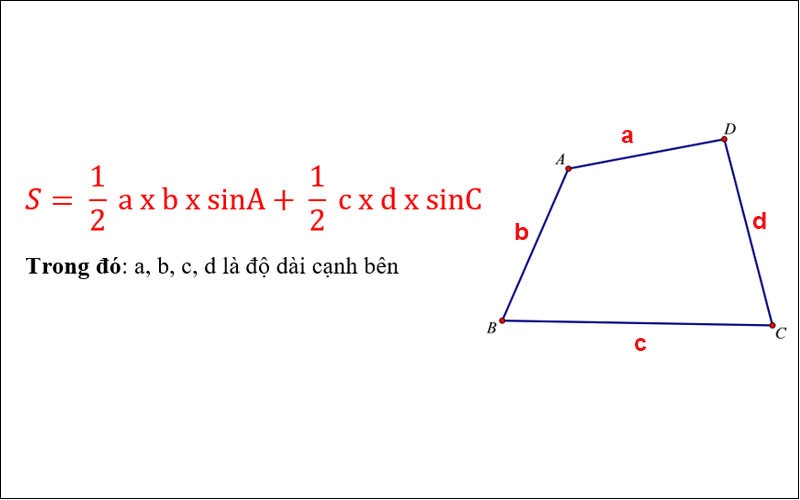
Để tính diện tích của một tứ giác khi chỉ biết độ dài của hai cạnh và góc giữa chúng, ta sử dụng công thức sau:
Diện tích của tứ giác ABCD = 1/2 × a × b × sin(C)
Trong đó:
- a, b là độ dài của hai cạnh
- C là góc giữa hai cạnh a và b
Cách sử dụng:
- Xác định độ dài của hai cạnh a và b của tứ giác ABCD.
- Tính góc C giữa hai cạnh a và b.
- Sau đó sử dụng công thức: Diện tích = a × b × sin(C)
- Tính toán và thu được diện tích của tứ giác.
Diện tích xung quanh hình chóp tứ giác đều
Để tính diện tích bề mặt xung quanh hình chóp tứ giác đều, ta sử dụng công thức sau:
S = 1/2 * C * d
Trong đó:
- S là diện tích bề mặt xung quanh của hình chóp
- C là chu vi của đáy hình chóp (tứ giác đều)
- d là chiều cao của hình chóp
Để tính chu vi C của đáy tứ giác đều: C = 4 * a (a là độ dài cạnh của đáy tứ giác đều)
Bài tập thực hành cách tính diện tích hình tứ giác
Sau khi đã nắm được các công thức tính diện tích hình tứ giác, hãy bắt đầu thực hành với những bài tập cơ bản dưới đây để rèn luyện kỹ năng tính toán và nâng cao khả năng giải quyết vấn đề một cách hiệu quả.
Bài 1: Tính diện tích của tứ giác ABCD biết các thông số sau:
- AB = 8 cm, BC = 6 cm, CD = 4 cm, DA = 10 cm
- Góc A = 60 độ, góc C = 120 độ
Bài 2: Tính diện tích hình thang PQRS biết:
- PQ = 5 cm, RS = 11 cm
- Đường cao h = 8 cm
Bài 3: Cho tứ giác lồi WXYZ với:
- Đường chéo WY = 12 cm, XZ = 16 cm
- Góc kẹp giữa 2 đường chéo 60 độ
Hãy tính diện tích của tứ giác WXYZ.
Bài 4: Tứ giác ABCD có các cạnh là: AB = 6 cm, BC = 8 cm, CD = 5 cm, DA = 7 cm. Hãy tính diện tích của tứ giác ABCD bằng cách chia nó thành 2 tam giác.
Bài 5: Cho một tứ giác có các đỉnh lần lượt là A(2,2), B(8,2), C(8,5) và D(2,5). Tính diện tích của tứ giác bằng công thức tọa độ.
Bài 6: Cho một tứ giác nội tiếp có các cạnh lần lượt là AB=6cm, BC=8cm, CD=5cm và DA=7cm. Tính diện tích của tứ giác sử dụng công thức Brahmagupta.

Một số lưu ý khi làm bài tập về diện tích của hình tứ giác
Việc nắm vững các công thức tính diện tích hình tứ giác là rất quan trọng, đặc biệt trong các kỳ kiểm tra và làm bài tập hình học. Dưới đây là một số lưu ý quan trọng khi làm bài tập về diện tích hình tứ giác:
- Xác định loại hình tứ giác: Trước tiên, hãy xác định chính xác loại hình tứ giác đang được đề cập, ví dụ như hình chữ nhật, hình bình hành, hình thoi, v.v. Điều này sẽ giúp bạn áp dụng công thức tính diện tích phù hợp.
- Nhận diện các thông số cần thiết: Tùy theo loại hình tứ giác, các thông số cần biết có thể là chiều dài, chiều rộng, đường chéo, góc, v.v. Hãy đảm bảo bạn đã xác định đủ các thông số này.
- Lựa chọn công thức chính xác: Dựa trên loại hình tứ giác và các thông số đã thu thập, hãy chọn công thức tính diện tích phù hợp. Các công thức có thể khác nhau giữa các loại hình tứ giác.
- Đối với các tứ giác có cấu trúc đặc biệt như hình chữ nhật, hình bình hành hoặc hình thoi, sử dụng công thức riêng cho từng loại sẽ giúp tính toán nhanh chóng và chính xác hơn.
- Đơn vị và độ chính xác: Lưu ý ghi rõ đơn vị đo (cm², m², etc.) và giữ đủ số chữ số thập phân phù hợp với yêu cầu của bài tập.
- Kiểm tra kết quả: Sau khi tính toán, hãy kiểm tra kết quả một lần nữa để đảm bảo không có sai sót. Nếu có thể, hãy vẽ hình minh hoạ để kiểm tra lại.
Bằng cách tuân theo những lời khuyên này, việc tính diện tích của hình tứ giác sẽ trở nên đơn giản và hiệu quả hơn.

Việc nắm vững các công thức và phương pháp tính diện tích hình tứ giác không chỉ giúp bạn giải quyết các bài toán hình học một cách nhanh chóng và chính xác mà còn là một kỹ năng quan trọng trong nhiều lĩnh vực thực tiễn. Hãy luyện tập thường xuyên với các dạng bài tập khác nhau để nâng cao kỹ năng và hiểu sâu hơn về công thức tính diện tích của nhiều loại tứ giác.
