Hình tam giác là gì?
Nghiên cứu chủ đề tính chu vi hình tam giác cho thấy đây là một trong những hình dạng quan trọng nhất trong toán học. Học về hình tam giác xây dựng nền tảng cho các môn học khó hơn như hình học và lượng giác.
Hình tam giác là một đa giác đơn giản nhất, bao gồm ba cạnh và ba góc được tạo thành khi ba điểm không thẳng hàng nối liền với nhau. Trong đó, ba cạnh của tam giác bất kỳ phải thỏa mãn điều kiện bất đẳng thức tam giác: a + b > c, a + c > b, b + c > a.
Tính chất:
- Tổng ba góc trong một tam giác luôn bằng 180 độ.
- Độ dài mỗi cạnh luôn lớn hơn hiệu số và nhỏ hơn tổng độ dài hai cạnh còn lại.
- Góc lớn nhất trong tam giác luôn đối diện với cạnh lớn nhất.
- Góc nhọn trong tam giác luôn đối diện với cạnh ngắn nhất.
- Hai tam giác có cùng độ dài ba cạnh thì bằng nhau.
- Hai tam giác có cùng độ dài hai cạnh và một góc kề cạnh đó thì bằng nhau.
- Hai tam giác có cùng độ dài một cạnh và hai góc kề cạnh đó thì bằng nhau.
Kim tự tháp Ai Cập, một trong những công trình kiến trúc vĩ đại nhất thế giới, được xây dựng dựa trên hình dạng tam giác.
Công thức tính chu vi hình tam giác bất kỳ
Công thức tính chu vi của một hình trong hình học phẳng sẽ bằng độ dài đường viền ngoài của hình. Do đó, trong trường hợp tam giác, chu vi sẽ bằng tổng của cả ba cạnh. Nếu một tam giác có ba cạnh a, b và c thì công thức tính là:
[Chu vi] P = a + b + c
Các cách tính chu vi hình tam giác đặc biệt
Ngoài trường hợp tam giác thường kể trên, người học cần nắm được các công thức tính chu vi hình tam giác có điều kiện đặc biệt để giải quyết các bài toán đòi hỏi suy luận phức tạp hơn.
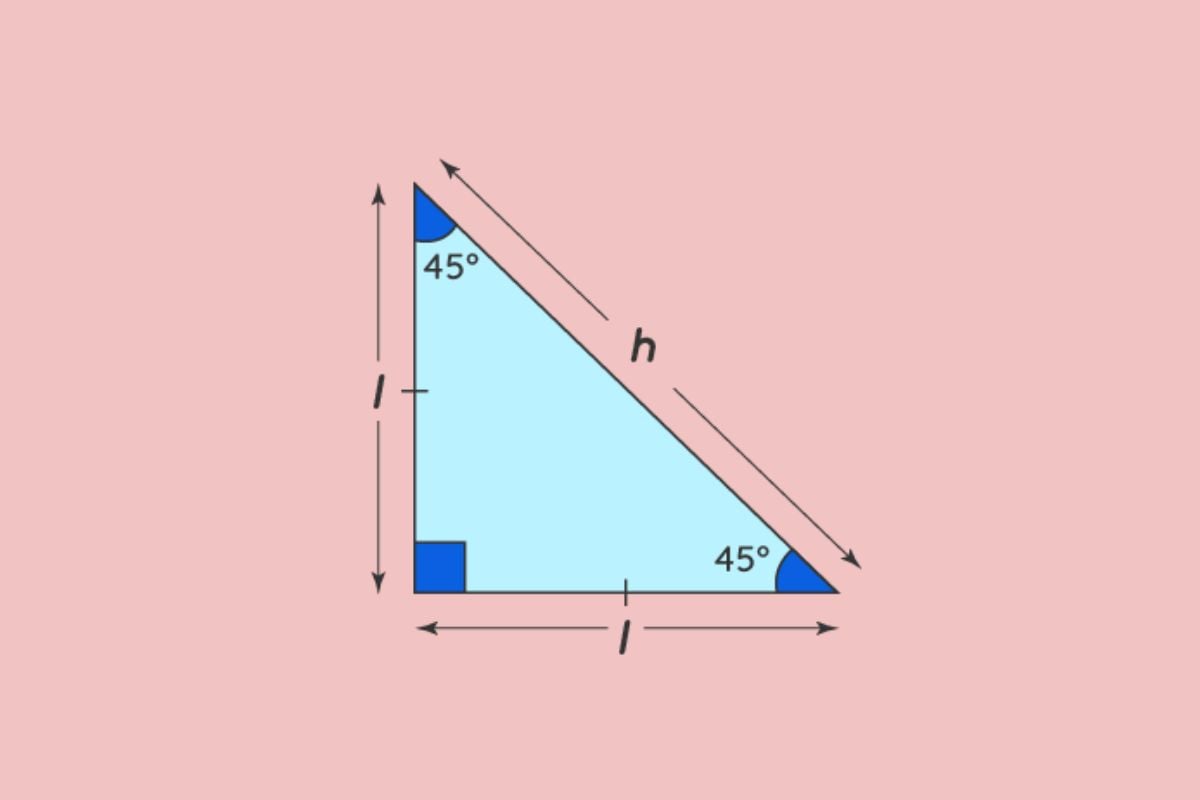
Công thức tính chu vi hình tam giác đều
Tam giác có ba cạnh bằng nhau và ba góc bằng nhau (60 °) được biết đến như một tam giác đều.
Xét tam giác đều ABC có mỗi cạnh có số đo là a.
Chu vi của một tam giác đều = a + a + a = 3a
Công thức tính chu vi hình tam giác cân
Một tam giác có hai cạnh bằng nhau được gọi là tam giác cân.
Vì hai cạnh của một tam giác bằng nhau nên ta có a = b
Chu vi của một tam giác cân = a + a + c = 2a + c
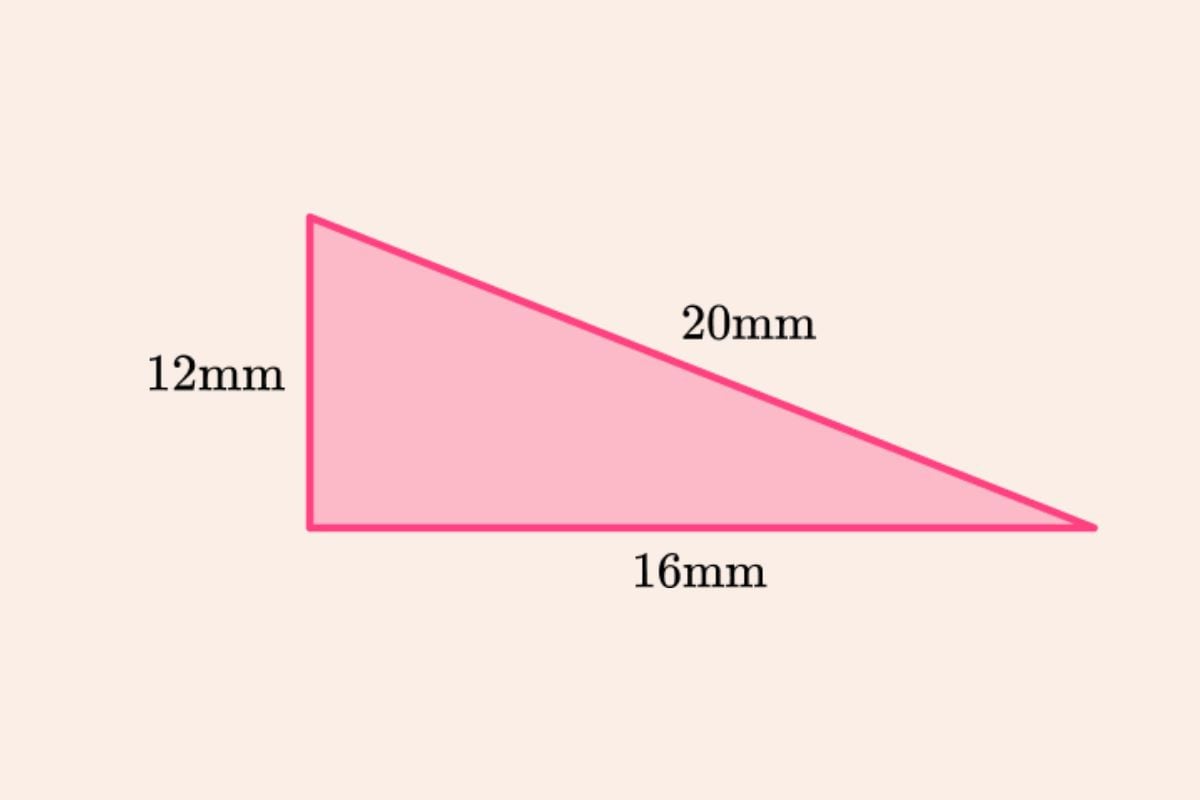
Công thức tính chu vi hình tam giác vuông
Một tam giác có một góc trong bằng 90 ° được gọi là tam giác vuông. Phía đối diện với góc vuông gọi là cạnh huyền. Hai cạnh còn lại được gọi là cạnh đáy của tam giác vuông. Một tam giác vuông có đáy (b), cạnh huyền (h) và đường vuông góc (p) là các cạnh của nó.
Theo định lý Pythagoras, chúng ta biết rằng:
h² = p² + b²
Do đó, chu vi của tam giác vuông = b + p + h = b + √p² + b²
Áp dụng các định lý toán học để tìm độ dài các cạnh hình tam giác
Việc tìm độ dài các cạnh hình tam giác đóng vai trò thiết yếu trong giải các bài toán liên quan đến diện tích, chu vi, góc,... Dưới đây, chúng tôi sẽ giới thiệu các định lý toán học thường được sử dụng để tìm độ dài các cạnh hình tam giác, giúp bạn dễ dàng giải quyết các vấn đề liên quan.
Định lý Pythagoras (cho tam giác vuông)
Nội dung: Trong một tam giác vuông, bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông.
Công thức: a^2 + b^2 = c^2
Áp dụng:
Trường hợp này chỉ áp dụng cho tam giác vuông.
Cần biết độ dài hai cạnh bất kỳ (cạnh góc vuông hoặc cạnh huyền) trong tam giác vuông.
Sau khi áp dụng công thức, ta sẽ tìm được độ dài cạnh còn lại trong tam giác vuông.
Ví dụ: Một tam giác vuông có hai cạnh góc vuông lần lượt dài 3cm và 4cm.
Áp dụng định lý Pythagoras kết hợp với công cụ máy tính online casio fx-580vn, ta có: c^2 = 3^2 + 4^2 = 9 + 16 = 25. Vậy, độ dài cạnh huyền của tam giác vuông đó là √25 = 5cm.
Định lý Sin
Nội dung: Tỷ số giữa độ dài một cạnh của tam giác và sin góc đối diện bằng tỷ số giữa chu vi tam giác và hai lần sin góc nhọn bất kỳ.
Công thức: a/sin A = b/sin B = c/sin C = 2R/sin A.sin B
Áp dụng:
Trường hợp này áp dụng cho tam giác bất kỳ.
Cần biết chu vi (R) của tam giác và sin của một góc (bất kỳ).
Sau khi áp dụng công thức, ta sẽ tìm được độ dài cạnh còn lại trong tam giác.
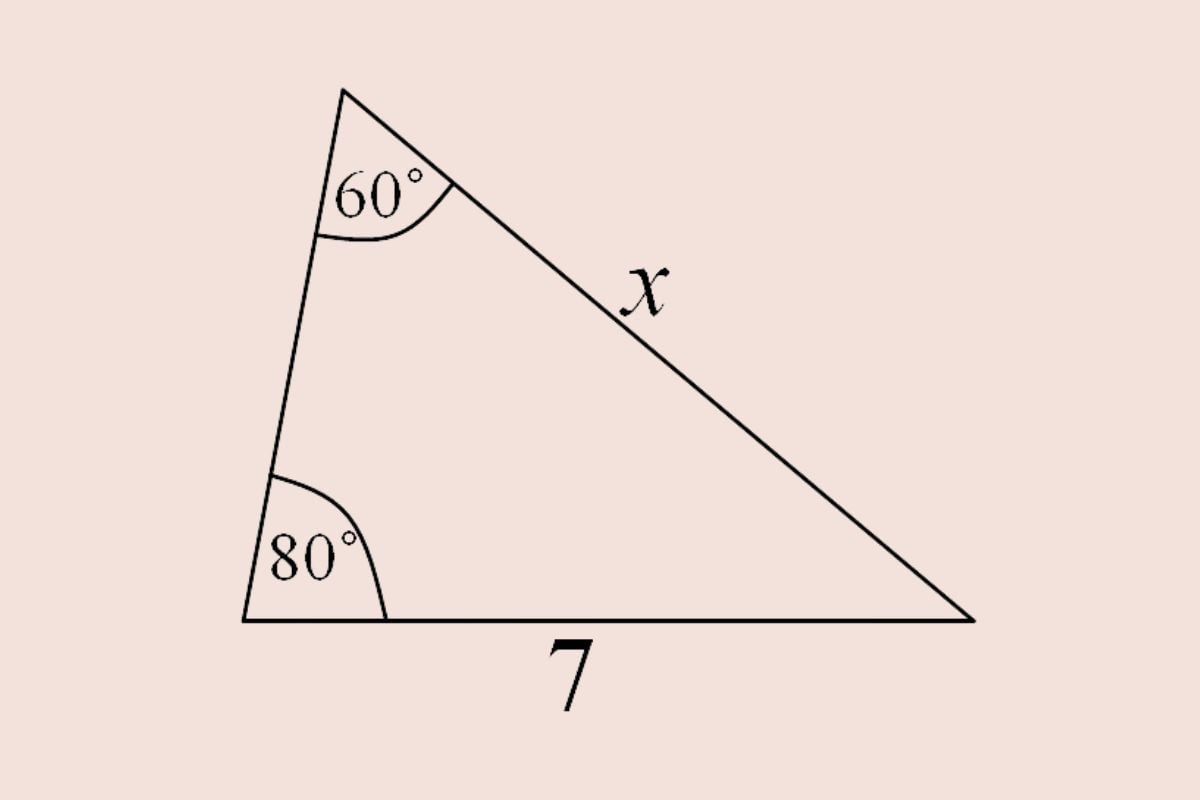
Ví dụ: Một tam giác có chu vi là 30cm và góc A là 60°.
Áp dụng định lý Sin, ta có: a/sin A = 30cm / (2 * sin 60°) = 30cm / (2 * 0,866) ≈ 17,1cm. Vậy, độ dài cạnh a của tam giác đó là 17,1cm.
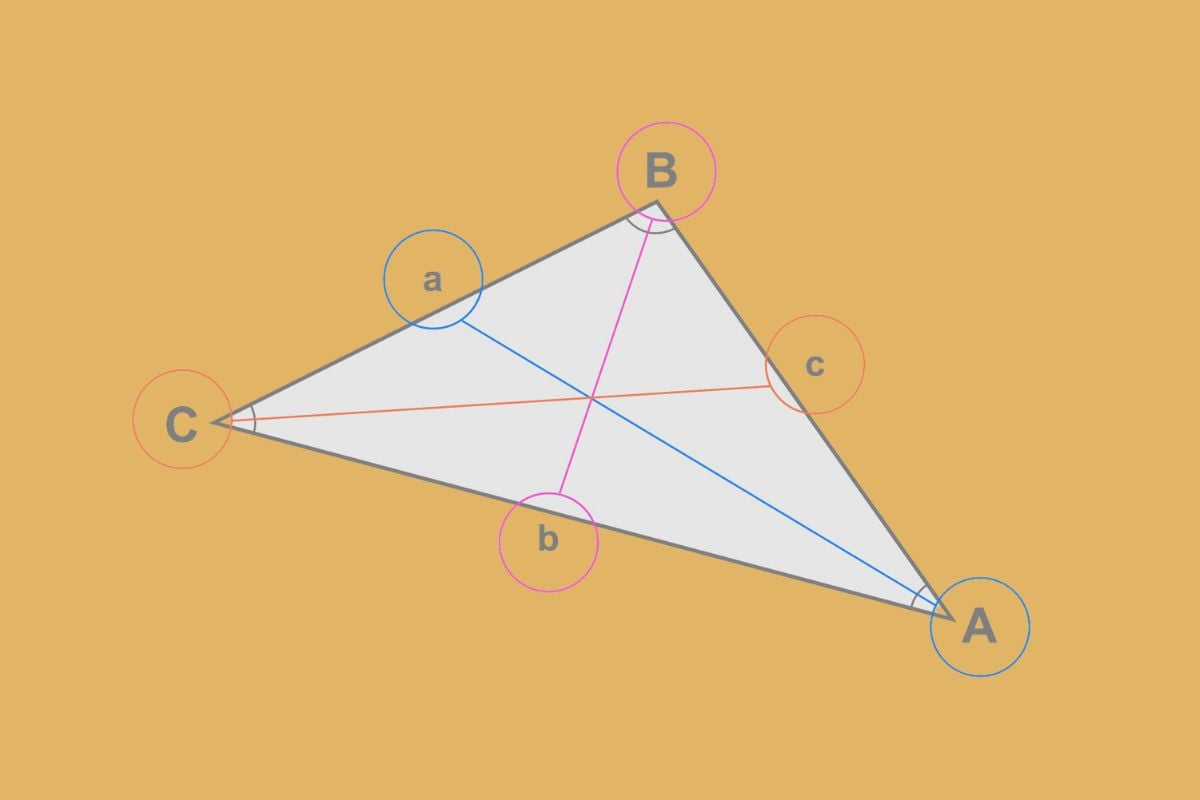
Định lý Cosin
Nội dung: Bình phương một cạnh của tam giác bằng tổng bình phương hai cạnh còn lại trừ đi hai lần tích của hai cạnh đó nhân với cosin góc xen giữa.
Công thức: a^2 = b^2 + c^2 - 2bc.cos C
Áp dụng:
Trường hợp này áp dụng cho tam giác bất kỳ.
Cần biết độ dài hai cạnh bất kỳ và cosin góc xen giữa của hai cạnh đó trong tam giác.
Sau khi áp dụng công thức, ta sẽ tìm được độ dài cạnh còn lại trong tam giác.
Ví dụ: Một tam giác có hai cạnh lần lượt dài 5cm và 7cm, góc xen giữa hai cạnh đó là 120°. Áp dụng định lý Cosin, ta có: a^2 = 5^2 + 7^2 - 2 * 5 * 7 * cos 120° ≈ 11,3cm. Vậy, độ dài cạnh a của tam giác đó là √11,3 ≈ 3,4cm.
Định lý Heron
Định lý Heron là một công thức toán học quan trọng được sử dụng để tính diện tích của tam giác khi biết độ dài ba cạnh của nó. Tuy nhiên, định lý này cũng có thể được ứng dụng để tìm độ dài các cạnh tam giác dựa trên diện tích đã biết và hai cạnh còn lại.
Nội dung: Diện tích của một tam giác bằng √s(s - a)(s - b)(s - c), trong đó s là nửa chu vi của tam giác (s = (a + b + c)/2).
Công thức: S = √s(s - a)(s - b)(s - c)
Áp dụng để tìm cạnh tam giác:
Bước 1: Biết diện tích (S) và hai cạnh (a, b) của tam giác.
Bước 2: Tính nửa chu vi (s): s = (a + b + c)/2
Bước 3: Thay S và s vào công thức Heron: c = √s(s - a)(s - b)(s - c)
Bước 4: Giải phương trình: Giải phương trình bậc hai để tìm giá trị c (độ dài cạnh cần tìm).
Lưu ý:
Cần đảm bảo điều kiện tam giác tồn tại: a + b > c, a + c > b và b + c > a.
Sử dụng máy tính hoặc công cụ giải phương trình để giải phương trình bậc hai ở bước 4.
Ví dụ: Cho một tam giác có diện tích là 20cm² và hai cạnh lần lượt dài là 5cm và 7cm. Tìm chiều dài cạnh thứ ba của tam giác đã nêu.
Giải:
Bước 1: S = 20cm², a = 5cm, b = 7cm
Bước 2: s = (a + b + c)/2 = (5 + 7 + c)/2 = 6 + c/2
Bước 3: 20 = √(6 + c/2)(6 + c/2 - 5)(6 + c/2 - 7)(6 + c/2 - c)
Bước 4: Giải phương trình bậc hai, ta tìm được c ≈ 8,89cm.
Bài tập nâng cao
Tìm chu vi của một hình đa giác có chiều dài các cạnh là 5 cm, 4 cm và 2 cm.
Giải:
Xác định độ dài các cạnh như sau:
a = 5 cm
b = 4cm
c = 2 cm
Chu vi = Tổng các cạnh = a + b + c = 5 + 4 + 2 = 11
Do đó, đáp án là 11 cm.
Tính chu vi của một tam giác đều có cạnh bằng 6cm.
Giải:
Vì một tam giác đều có tất cả các cạnh bằng nhau.
Do đó, a = 6
Chu vi tam giác đều= a + b + c = a + a + a = 3a
= 3 xa
= 3 x 6
= 18cm
Tính chu vi của một tam giác vuông có đáy là 3 cm và chiều cao là 4 cm.
Đầu tiên, sử dụng định lý Pythagore, tính cạnh huyền của tam giác vuông.
h =√(cơ số 2 +đường vuông góc 2 )
h = √(3 2 +4 2 )
h = √(9 + 16)
h = √25
Hoặc h = 5 cm
Vậy chu vi hình tam giác = 3 + 4 + 5 = 12 cm.
Tìm chu vi của một tam giác cân có cạnh thứ ba bằng 6 cm, cạnh thứ ba là 8 cm.
Giải:
Tam giác cân sẽ có hai cạnh bằng nhau.
Vậy a = 6, b = 6 và c = 8
Chu vi của một tam giác cân= a +b + c = a + a + c = 2a + c
= 2 x 6 + 8
= 12 + 8
= 20cm
Tìm chiều dài cạnh còn thiếu của biển báo đường hình tam giác có chu vi là 48 cm, hai cạnh mỗi cạnh 17 cm.
Giải:
Gọi độ dài cạnh còn thiếu là b.
Cho trước chu vi = 48 cm
Độ dài hai cạnh bằng nhau = 17cm
Chu vi tam giác = tổng độ dài ba cạnh
48 = 17 + 17 + b
48 = 34 + b
b = 14
Do đó, b = 14 cm
Đáp án: Chiều dài cạnh còn thiếu = 14cm.

Tìm chu vi tam giác vuông PQR có PR là cạnh huyền và có cạnh PQ = 4 cm, QR = 3 cm.
Giải:
Cho trước, PQ = 4 cm, QR = 3 cm, PR = ?
Để tính chu vi của tam giác, chúng ta cần biết cả ba cạnh.
Chúng ta sẽ tính độ dài cạnh huyền (PR) bằng định lý Pythagoras.
PR 2 = PQ 2 + QR 2
PR² = 4² + 3²
PR² = 16 + 9
Do đó PR = √25 cm
PR = 5 cm.
Bây giờ chúng ta có thể tính chu vi của tam giác.
Chu vi tam giác PQR = Tổng ba cạnh
= 3 + 4 + 5 = 12
Do đó, chu vi là 12 cm.
Tính chu vi hình tam giác có 3 cạnh đều bằng 10 cm.
Giải : Vì ba cạnh bằng nhau nên tam giác đó là tam giác đều. Tức là a = b = c = 10 cm
Chu vi = a + b + c
= 10 + 10 + 10
= 30
Chu vi = 30 cm.
Chu vi của một sợi dây hình chữ nhật là 297 cm. Cùng một sợi dây được uốn thành hình tam giác đều. Tìm độ dài mỗi cạnh của nó.
Giải:
Biết rằng, chu vi hình chữ nhật = chiều dài của dây
Chiều dài dây đã dùng = Chu vi hình tam giác
Chu vi của một tam giác đều = 3 × a
297 = 3 × a
a= 99
Trả lời: Độ dài mỗi cạnh của tam giác = 99 cm
Độ dài cạnh còn thiếu của một tam giác có chu vi là 40 cm và hai cạnh dài 10 cm là bao nhiêu?
Giải :
Cho trước, chu vi = 40 cm
Chiều dài 2 cạnh bằng nhau tức là 10 cm.
Vậy tam giác đó là tam giác cân.
Sử dụng công thức: P = 2a + b
40 = 2 * 10 + b
40 = 20 + b
hoặc b = 20
Chiều dài cạnh còn thiếu là 20 cm.
Bài viết trên đã cung cấp đầy đủ và chi tiết từng trường hợp kèm theo công thức tính chu vi hình tam giác. Ngoài ra còn kèm thêo các ví dụ minh họa cụ thể giúp bạn dễ dàng hiểu và áp dụng kiến thức vào thực tế.
