Số nguyên tố là gì? Cách tính số nguyên tố siêu đơn giản

Số nguyên tố là gì? 

Muốn định nghĩa số nguyên tố là gì thì khá đơn giản. Số nguyên tố là số chỉ có hai ước số (các số nhân với nhau để tạo thành số) là chính số đó và 1.

Các tính chất của số nguyên tố

Từ khái niệm số nguyên tố là gì có thể thấy đây là số có thể chia cho chính nó và cho 1 mà không có số dư. Vì vậy, nếu một số có thể chia cho nhiều số hơn chính nó và 1 thì đó không phải là số nguyên tố và được gọi là hợp số. Số 1 không phải là số nguyên tố vì 1 chỉ chia hết cho 1 nên không có hai ước. Như vậy, số nguyên tố là số lớn hơn 1.

Một số tính chất của số nguyên tố đó là:

Số nguyên tố luôn chỉ có đúng hai ước

• Ước số thứ nhất: Luôn là 1.
• Ước số thứ hai: Chính là bản thân số đó.

Ví dụ: Số 7 là số nguyên tố vì nó chỉ chia hết cho 1 và chính nó (7:1 = 7).

Số nguyên tố luôn lớn hơn 2 nếu là số lẻ

Các số nguyên tố lớn hơn 2 đều có dạng 4n + 1 hoặc 4n - 1 (n là số nguyên).

Ví dụ: Số 11 là số nguyên tố vì nó là số lẻ (11 > 2 và 11 = 4 * 2 + 3).

Số lượng các số nguyên tố là vô hạn

Khám phá số nguyên tố là gì chúng ta sẽ thấy dãy số này trải dài vô tận, không có điểm dừng. Tổng của hai số nguyên tố liên tiếp luôn là một số chẵn.

Ví dụ: 5 + 7 = 12 (chẵn).

Mọi số nguyên tố đều lớn hơn 1

Số 1 không được xếp vào nhóm số nguyên tố. Điểm đặc biệt của số nguyên tố đó là hai số liên tiếp luôn chênh lệch nhau 2 đơn vị:

Ví dụ: 17 và 19, 199 và 211, 191 và 193.

Số chia hết cho nhiều hơn 2 số nguyên tố khác nhau không thể là số nguyên tố

Ví dụ: 8 = 2 * 2 * 2 không phải là số nguyên tố.

Số nguyên tố khác gì số nguyên?

Trong quá trình tìm hiểu số nguyên tố là gì, nhiều người vẫn còn nhầm lẫn với khái niệm số nguyên. Bảng dưới đây sẽ giúp bạn phân biệt rõ ràng giữa số nguyên tố và số nguyên.

Cách tính số nguyên tố đơn giản, dễ hiểu

Sau khi nắm được số nguyên tố là gì, chúng ta hãy tìm hiểu hai phương pháp chính để tính số nguyên tố.

Phương pháp 1: Sử dụng bảng số nguyên tố

Phương pháp 2: Chia thử

Phương pháp chia thử là phương pháp kiểm tra xem một số có chia hết cho các số nguyên tố nhỏ hơn nó hay không.

Các bước thực hiện:

1. Lấy số cần kiểm tra chia cho 2.
2. Nếu chia hết cho 2 thì số đó không phải là số nguyên tố. Ngược lại, ta tiếp tục chia số đó cho 3.
3. Tiếp tục chia số đó cho các số nguyên tố nhỏ hơn cho đến khi tìm được ước số lớn hơn căn bậc hai của số cần kiểm tra.
4. Nếu không tìm được ước số nào, thì số đó là số nguyên tố.

Ví dụ: Kiểm tra xem số 19 có phải là số nguyên tố hay không.

Chia 19 cho 2: 19 không chia hết cho 2.

Chia 19 cho 3: 19 không chia hết cho 3.

Chia 19 cho 5: 19 không chia hết cho 5.

Chia 19 cho 7: 19 không chia hết cho 7.

Chia 19 cho các số nguyên tố nhỏ hơn 7 (tức là 11 và 13): 19 không chia hết cho 11 và 13.

Vậy 19 là số nguyên tố.

Các dạng bài tập thường gặp về số nguyên tố

Chủ đề số nguyên tố là gì quan trọng trong toán học với nhiều ứng dụng thực tế. Dưới đây là một số dạng bài tập phổ biến mà người học thường gặp:

Kiểm tra một số bất kỳ có phải là số nguyên tố hay không

Dạng 1: Xác định trực tiếp: Kiểm tra xem số đó có chia hết cho các số nguyên tố nhỏ hơn chính nó (từ 2 đến √n) hay không. Số được cho thỏa mãn nếu nó không chia hết cho bất kỳ số nào.

Ví dụ: Kiểm tra xem 17 có phải là số nguyên tố hay không.

Giải:

Chia 17 cho các số nguyên tố nhỏ hơn 17: 17 / 2 = 8 dư 1, 17 / 3 = 5 dư 2, 17 / 5 = 3 dư 2, 17 / 7 = 2 dư 3.

Do 17 không chia hết cho bất kỳ số nguyên tố nào nhỏ hơn 17, nên 17 là số nguyên tố.

Dạng 2: Sử dụng các định lý về số nguyên tố:

• Định lý Fermat nhỏ: Nếu a là số nguyên tố và p là số nguyên tố lẻ bất kỳ, thì a^(p-1) ≡ 1 (mod p).
• Định lý Wilson: Nếu p là số nguyên tố lẻ, thì (p-1)! ≡ -1 (mod p).

Ví dụ: Kiểm tra xem 13 là số nguyên tố hay không.

Giải:

Áp dụng định lý Fermat nhỏ với a = 2 và p = 13: 2^(13-1) ≡ 1 (mod 13) ⇔ 8192 ≡ 1 (mod 13).

Do 8192 chia 13 dư 1, nên 13 là số nguyên tố.

Phân tích số nguyên thành tích các số nguyên tố

Dạng 1: Phân tích theo phương pháp "lần lượt chia hết cho các số nguyên tố": Chia số nguyên tố cho các số nguyên tố nhỏ hơn chính nó cho đến khi thương số bằng 1.

Ví dụ: Phân tích 120 thành tích các số nguyên tố.

Giải:

120 = 2^3 * 3 * 5.

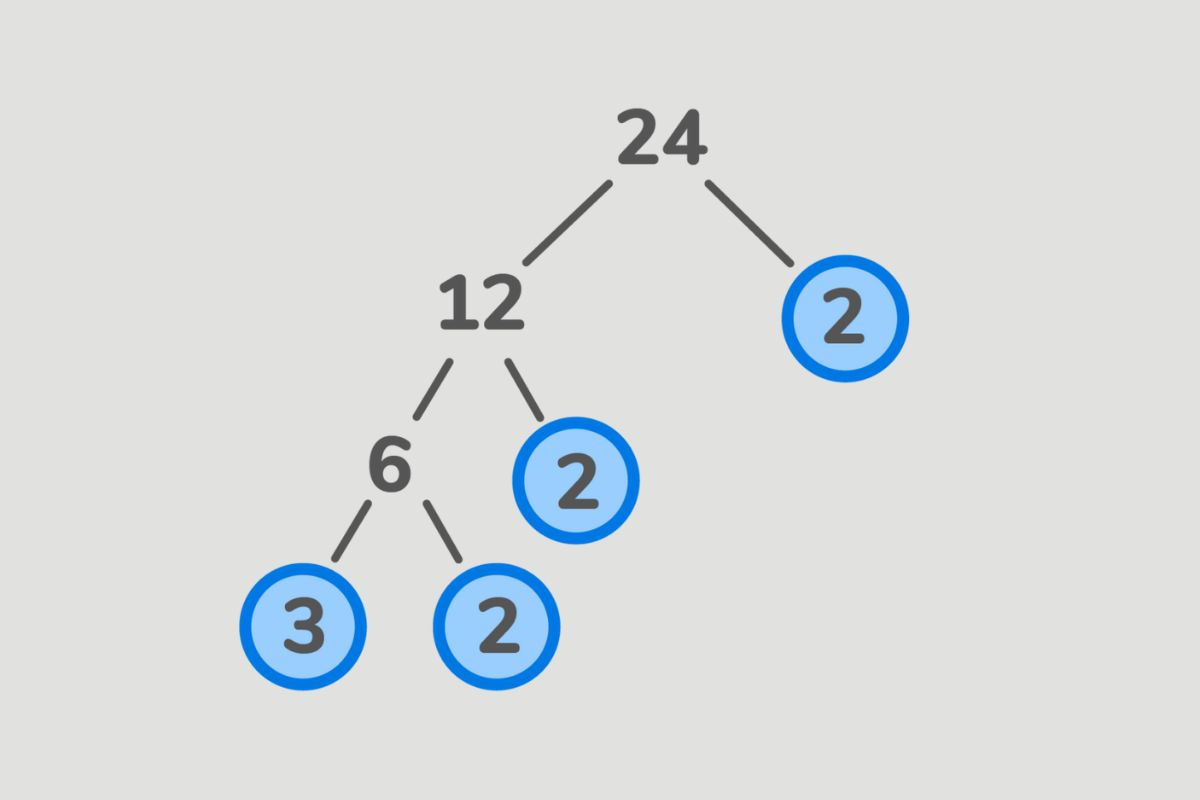
Dạng 2: Sử dụng "cây số nguyên tố": Vẽ một cây với số cần phân tích là gốc, các số nguyên tố nhỏ hơn là các nhánh. Gạch chéo các nhánh sao cho tích của chúng bằng số cần phân tích.

Ví dụ: Phân tích 180 thành tích các số nguyên tố.

180

/ \

2 90

/ \

2 45

/ \

3 15

/ \

5 3

\

1

180 = 2^2 * 3^2 * 5.

Ước số chung lớn nhất (ƯSCLN) và Ước số chung nhỏ nhất (ƯCNN)

Dạng 1: Tìm ƯSCLN và ƯCNN của hai số bằng cách:

• Phân tích một số bất kỳ thành tích các số nguyên tố.
• Lấy tích các số nguyên tố chung với số mũ nhỏ nhất của mỗi số.
• Lấy tích các số nguyên tố không chung.

Ví dụ: Tìm ƯSCLN và ƯCNN của 18 và 30.

Giải:

18 = 2 * 3^2, 30 = 2 * 3 * 5.

ƯSCLN(18, 30) = 2 * 3 = 6.

ƯCNN(18, 30) = 30.

Dạng 2: Sử dụng thuật toán Euclid:

Chia số lớn cho số nhỏ.

• Lấy số dư làm số chia mới, số chia cũ làm số bị chia.
• Lặp lại bước 2 cho đến khi số dư bằng 0.
• ƯSCLN của hai số ban đầu bằng số chia cuối cùng.

Ví dụ: Tìm ƯSCLN của 48 và 18.

Giải:

48 / 18 = 2 dư 12.

18 / 12 = 1 dư 6.

12 / 6 = 2.

6 / 2 = 3.

Do 2 là số dư cuối cùng, nên ƯSCLN(48, 18) = 2.

Kết luận:

ƯSCLN(48, 18) = 2.

Tìm số nguyên tố thứ n

Dạng 1: Sử dụng công thức:

Số nguyên tố thứ n là số nguyên tố nhỏ nhất lớn hơn hoặc bằng n, với n là số nguyên dương.

Ví dụ: Tìm số nguyên tố thứ 10.

Giải:

Sử dụng bảng minh họa cho sẵn, ta thấy số thỏa mãn yêu cầu của đề bài là 19.

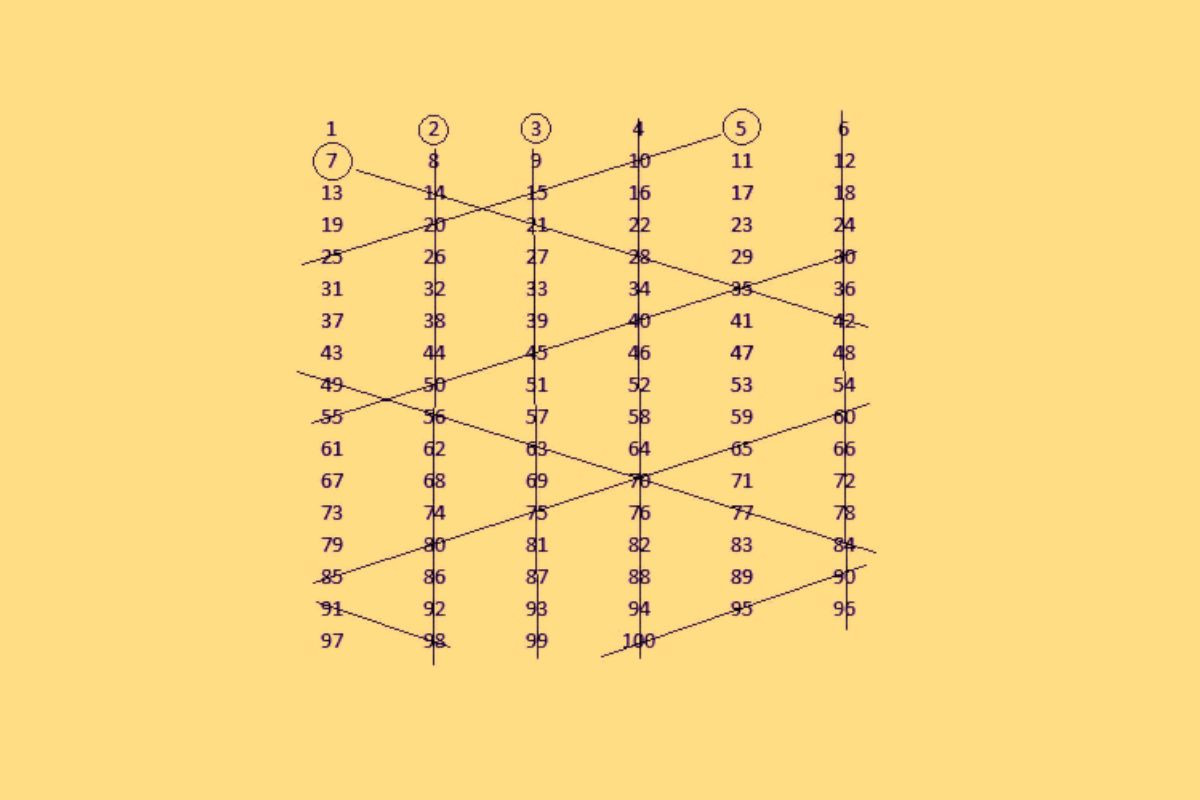
Dạng 2: Sử dụng sàng lọc Eratosthenes:

• Tạo một danh sách các số nguyên dương từ 2 đến n.
• Gạch chéo số bình phương của các số nguyên tố nhỏ hơn √n.
• Gạch chéo các số còn lại theo từng bước:
• Lặp từ số nhỏ nhất chưa bị gạch chéo, gạch chéo các bội số của nó.
• Chuyển sang số tiếp theo chưa bị gạch chéo, lặp lại bước trên.
• Các số không bị gạch chéo là các số nguyên tố nhỏ hơn hoặc bằng n.

Ví dụ: Tìm số nguyên tố thứ 20.

2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20

X X X X X X X X X X X X X X X X X X X

2 3 5 7 11 13 17 19

X X X X X X X X

2 3 5 7 11 13 17

X X X X X

2 3 5 7 11 13

X X X X

2 3 5 7 11

X X X

2 3 5 7

X X

2 3 5

X X

2 3

X

Số nguyên tố thứ 20 là 73.

Tìm cặp số nguyên tố cùng nhau

Dạng 1: Hai số nguyên tố được gọi là nguyên tố cùng nhau nếu ƯCLN của chúng bằng 1.

Ví dụ: Xác định xem 7 và 13 có phải là số nguyên tố cùng nhau hay không.

Giải:

ƯCLN(7, 13) = 1.

Vậy 7 và 13 là số nguyên tố cùng nhau.

Dạng 2: Sử dụng các tính chất của số nguyên tố.

Hai số nguyên tố có dạng 4n + 1 và 4n + 3 luôn nguyên tố cùng nhau (n là số nguyên bất kỳ).

Hai số p và q nguyên tố cùng nhau nếu p^2 không chia hết cho q.

Ví dụ: Xác định xem 5 và 11 có phải là số nguyên tố cùng nhau hay không.

Giải:

5 và 11 đều có dạng 4n + 1 (với n = 1 và n = 2).

Do đó, 5 và 11 là số nguyên tố cùng nhau.

Giải các phương trình chứa số nguyên tố

Dạng 1: Phương trình bậc nhất chứa một số nguyên tố: Giải phương trình như bình thường, sau đó kiểm tra xem giá trị thu được có thỏa mãn điều kiện đề bài hay không.

Ví dụ: Giải phương trình 3x + 5 = 14.

Giải:

3x = 9 ⇔ x = 3.

Giá trị x = 3 thỏa mãn điều kiện đề bài.

Dạng 2: Phương trình chứa nhiều số nguyên tố: Phân tích các số này thành tích các thừa số nguyên tố, sau đó giải phương trình như bình thường.

Ví dụ: Giải phương trình 2x^2 + 3x - 5 = 0.

Phân tích vế trái:

2x^2 + 3x - 5 = (2x - 1)(x + 5)

Giải phương trình:

(2x - 1)(x + 5) = 0 ⇔ 2x - 1 = 0 hoặc x + 5 = 0

TH1: 2x - 1 = 0 ⇔ x = 1/2

TH2: x + 5 = 0 ⇔ x = -5

Kết luận:

Phương trình có hai nghiệm: x = 1/2 và x = -5.

Một số khái niệm liên quan và ví dụ minh họa

Bên cạnh số thông tin số nguyên tố là gì, muốn hiểu sâu và nắm chắc các kiến thức thuộc chủ đề này, người học cần biết các khái niệm liên quan sau:

Số siêu nguyên tố

Số siêu nguyên tố là số mà tất cả các ước số nguyên tố của nó cũng là số nguyên tố. Ví dụ: 3, 5, 7.

Thừa số nguyên tố là gì

Thừa số nguyên tố là một số nguyên tố được nhân với một hoặc nhiều số nguyên tố khác để tạo thành một số nguyên tố. Ví dụ: 2 x 3 = 6, trong đó 2 và 3 là các thừa số nguyên tố.

Số nguyên tố cùng nhau là gì

Nếu ước số chung lớn nhất (ƯCLN) của hai số nguyên tố bằng 1 thì chúng là nguyên tố cùng nhau. Ví dụ: 2 và 3 là hai số nguyên tố cùng nhau, vì ƯCLN(2, 3) = 1.

Tích các thừa số nguyên tố

Tích các thừa số nguyên tố là kết quả của việc nhân tất cả các thừa số của một số nguyên tố. Ví dụ: số 12 có các thừa số nguyên tố là 2 và 3, do đó tích các thừa số nguyên tố của nó là 2 x 3 = 6.

Một số câu hỏi thú vị về số nguyên tố

Dưới đây là một số câu hỏi thú vị giúp bạn hiểu chi tiết hơn về số nguyên tố là gì.

Có bao nhiêu số nguyên tố?

Đào sâu chủ đề số nguyên tố là gì thì đây là một câu hỏi hóc búa mà các nhà toán học đã tranh luận trong nhiều thế kỷ. Hiện tại, vẫn chưa biết chính xác có bao nhiêu số thuộc danh sách này. Theo Euclid, số nguyên tố vô hạn nhưng vẫn chưa có bằng chứng hoàn chỉnh nào cho điều này.

Số nguyên tố có ứng dụng gì trong thực tế?

Sau khi học chủ đề số nguyên tố là gì bạn sẽ thấy nó có nhiều ứng dụng trong thực tế, bao gồm:

• Mã hóa dữ liệu (mật mã RSA)
• Xác minh tính toàn vẹn dữ liệu (ký số điện tử)
• Tìm kiếm thông tin (thuật toán tìm kiếm)
• Thiết kế hệ thống mạng (phân chia mạng)

Số nguyên tố nhỏ nhất là số nào?

Đó là số 2. Đây là số nguyên tố duy nhất là số chẵn. Các số nguyên tố khác đều là số lẻ.

Số nguyên tố lớn nhất đã biết là số nào?

Không có số nguyên tố lớn nhất. Các nhà toán học liên tục tìm kiếm các số lớn hơn. Hiện nay, số nguyên tố lớn nhất đã biết là 2^82,589,933 - 1, có 24,862,048 chữ số khi viết ở hệ thập phân. Số nguyên tố này được tìm thấy bởi Patrick Laroche vào năm 2018.

Tại sao chỉ có số 2 là số nguyên tố chẵn?

Từ định nghĩa số nguyên tố là gì có thể thấy bất kỳ số chẵn nào (ngoài 2) đều có thể chia hết cho 2, do đó nó không phải là số nguyên tố.

Có phải mọi số nguyên tố lớn hơn 3 đều nằm cạnh một số chia hết cho 6?

Thực tế, không hẳn là vậy. Ví dụ, số nguyên tố 5 không nằm cạnh một số chia hết cho 6. Hai số nguyên tố liền kề nhau luôn có dạng 6n ± 1 (với n là số nguyên). Do đó, hai số nguyên tố liền kề nhau luôn có hiệu là 2 hoặc 4. Nếu một số nguyên tố lớn hơn 3 nằm cạnh một số chia hết cho , thì hiệu của hai số đó phải là bội số của 6, mâu thuẫn với điều kiện hiệu là 2 hoặc 4.

Có một số nguyên tố nào mà khi viết ngược lại vẫn là số nguyên tố không?

Câu trả lời là CÓ. Trong bài học số nguyên tố là gì, người học cần biết các số mà khi viết ngược lại vẫn là số nguyên tố được gọi là số nguyên tố palindrome. Ví dụ, số 11, 13, 17, 193, 353, 739, 997 là những số palindrome.

Có phải mọi số nguyên tố đều có thể biểu diễn dưới dạng tổng của hai số chính phương không?

Có. Đây là định lý Fermat được chứng minh bởi Pierre de Fermat. Tuy nhiên, vẫn chưa có công thức nào để xác định hai số chính phương cụ thể nào tạo thành tổng đó cho một số nguyên tố nhất định

Số nguyên tố được sử dụng để xây dựng các thuật toán mã hóa an toàn, phân tích các số này được sử dụng để giải các phương trình Diophantine. Hiểu rõ số nguyên tố là gì không chỉ giúp học sinh giải quyết các dạng bài tập liên quan mà còn có thể là tiền đề nghiên cứu các ứng dụng của nó vào các lĩnh vực thực tế.