Giải đáp: I là tập hợp số gì? Tập hợp I có số 0 không? Tất tần tật về tập I

I là tập hợp số gì? Ví dụ 

I là tập hợp số gì? Đây là thông tin mà nhiều người quan tâm và mong muốn có câu trả lời chính xác khi tìm hiểu về các tập hợp số trong toán học. Theo quy ước, I là ký hiệu của tập hợp số vô tỉ. Số vô tỉ là những số thực không thể biểu diễn dưới dạng phân số a/b với a và b là các số nguyên và b # 0 được. Thay vào đó, các số vô tỉ là những số được biểu diễn dưới dạng số thập phân vô hạn không tuần hoàn.

Các ví dụ về tập hợp I:

• Số pi, ký hiệu là π
• Căn bậc của 2, ký hiệu √2
• Số Euler e

Số vô tỉ xuất hiện trong nhiều lĩnh vực toán học, bao gồm hình học, số học và giải tích. Chúng đóng vai trò quan trọng trong việc hiểu rõ hơn về cấu trúc của các số thực và giúp giải quyết nhiều bài toán phức tạp mà các số hữu tỉ không thể giải quyết được. Do đó, việc tìm hiểu I là tập hợp số gì và nắm rõ các tính chất của tập hợp I là rất cần thiết.

Phân biệt số hữu tỉ Q và số vô tỉ I

Khi tìm hiểu Q là tập hợp số gì, I là tập hợp số gì, nhiều người dễ bị nhầm lẫn giữa số vô tỉ và số hữu tỉ. Thực tế, số hữu tỉ là những số có thể viết được dưới dạng phân số, còn số vô tỉ là những số không thể viết được dưới dạng phân số mà chỉ được viết dưới dạng số thập phân vô hạn không tuần hoàn.

Dưới đây là những điểm khác nhau cơ bản giữa số hữu tỉ và số vô tỉ mà bạn có thể tham khảo:

Mối quan hệ giữa tập I với các tập hợp số khác

Để dễ dàng giải quyết các dạng toán liên quan đến tập hợp I, ngoài việc tìm hiểu I là tập hợp số gì, bạn cũng cần nắm rõ mối quan hệ giữa tập hợp I với những tập hợp số khác trong toán học. Dưới đây là mối quan hệ giữa tập I với tập R, Q và Z mà bạn có thể tham khảo:

Mối quan hệ giữa tập I với tập R 

Như đã tìm hiểu ở trên, I là ký hiệu tập hợp số vô tỉ, còn R là ký hiệu tập hợp số thực. Theo quy ước toán học, tập hợp I là tập con của tập số thực R. Điều này có nghĩa là mọi số vô tỉ đều là số thực nhưng không phải mọi số thực đều là số vô tỉ.

Ký hiệu: I ⊂ R

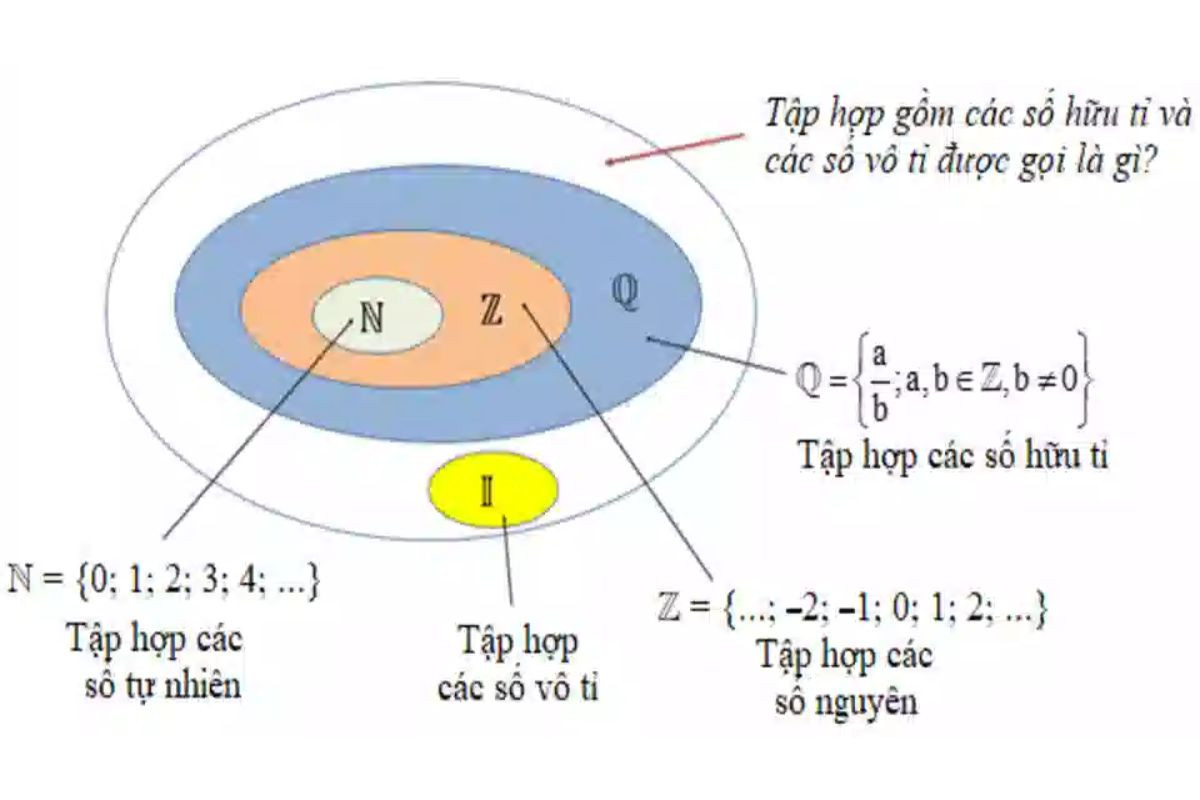
Mối quan hệ giữa tập I với tập Q

Sau khi xác định rõ I là tập hợp số gì, Q là tập hợp số gì và biết cách phân biệt giữa hai loại số này, bạn cũng sẽ xác định được mối quan hệ giữa tập hợp I với tập Q. Theo đó, tập hợp số hữu tỉ Q và tập hợp số vô tỉ I không giao nhau, có nghĩa là không có tập hợp nào là con của tập hợp nào.

Thay vào đó, tập hợp I và tập hợp Q bổ sung cho nhau để tạo nên tập hợp số thực R. Điều này có nghĩa là bất kỳ số thực nào cũng là số hữu tỉ hoặc số vô tỉ. Sự kết hợp giữa số hữu tỉ và số vô tỉ giúp bạn có cái nhìn toàn diện về các số trong toán học.

Mối quan hệ giữa tập hợp I với tập Z

Trong toán học, I là ký hiệu số vô tỉ, còn Z là tập hợp số nguyên. Thực tế, không có số nào vừa là số nguyên vừa là số vô tỉ. Số nguyên là các số đếm được và được sắp xếp một cách rời rạc trên trục số, số vô tỉ là các số không thể đếm được và lấp đầy trục số một cách liên tục.

Do đó, tập hợp I và tập hợp số nguyên Z không giao nhau, tức là không có tập hợp nào là con của tập hợp nào. Tuy nhiên, xét trên tổng thể thì cả tập hợp số vô tỉ I và tập hợp số nguyên Z đều thuộc tập hợp số thực R.

Tính chất của tập hợp I trong toán học 

Bên cạnh việc tìm hiểu I là tập hợp số gì, bạn cũng cần nắm rõ các tính chất của tập hợp I để vận dụng giải các bài toán có liên quan. Tập hợp số vô tỉ I có những tính chất cơ bản sau đây:

• Tập hợp số vô tỉ I là những số thực không thể biểu diễn dưới dạng phân số.
• Số vô tỉ có dạng thập phân vô hạn không tuần hoàn, nghĩa là các chữ số sau dấu phẩy tiếp tục mãi mãi mà không lặp lại theo một mẫu nhất định.
• Tập hợp số vô tỉ là tập hợp không đếm được, nghĩa là không thể liệt kê tất cả các số vô tỉ theo một thứ tự tuần tự
• Giữa hai số thực bất kỳ, luôn tồn tại ít nhất một số vô tỉ. Hơn nữa, giữa hai số hữu tỉ bất kỳ cũng luôn tồn tại ít nhất một số vô tỉ.
• Tổng của hai số vô tỉ có thể là số hữu tỉ, ví dụ √2 + (-√2) = 0
• Hiệu của hai số vô tỉ cũng có thể là số hữu tỉ, ví dụ √2 - √2 = 0
• Tích của hai số vô tỉ cũng có thể là số hữu tỉ, ví dụ √2 x √2 = 2
• Thương của hai số vô tỉ cũng là số hữu tỉ, ví dụ √2 : √2 = 1
• Một tập con của số vô tỉ bao gồm các số không phải là nghiệm của bất kỳ phương trình đại số với hệ số hữu tỉ.

Ý nghĩa của tập hợp số vô tỉ I trong toán học

Sau khi đã nắm rõ I là tập hợp số gì, bạn sẽ biết được tính ứng dụng của tập hợp I trong các lĩnh vực cụ thể. Tập hợp số vô tỉ I có vai trò và ý nghĩa quan trọng trong toán học, được thể hiện qua nhiều khía cạnh khác nhau như:

• Hoàn thiện trục số thực: Số vô tỉ I cùng số hữu tỉ Q tạo thành toán bộ tập hợp số thực R. Sự tồn tại của các số vô tỉ giúp lấp đầy các khoảng trống trên trục số thực, đảm bảo rằng trục số này là liên tục và không bị gián đoạn.
• Giải quyết các phương trình đại số: Nhiều phương trình đại số không thể có nghiệm là số hữu tỉ. Ví dụ, phương trình x^2 - 2 có nghiệm là √2, đây là số vô tỉ.
• Mở rộng khái niệm đo lường và hình học: Không chỉ trong đại số, số vô tỉ còn xuất hiện trong hình học và đo lường. Ví dụ, tỉ số giữa chu vi và đường kính của một đường tròn là π, đây là số vô tỉ. Chiều dài của đường chéo của một hình vuông với cạnh bằng 1 là √2, đây cũng là số vô tỉ.
• Cơ sở cho các hằng số toán học quan trọng: π xuất hiện trong nhiều công thức liên quan đến hình học, lượng giác,... e là cơ sở của logarithm tự nhiên, xuất hiện trong các phép tính về lãi kép, giải thích,...
• Phát triển lý thuyết số và các lĩnh vực toán học khác: Số vô tỉ đóng vai trò quan trọng trong lý thuyết số, đặc biệt là trong việc nghiên cứu các tính chất của các dãy và chuỗi số. Việc phân loại số vô tỉ mở ra nhiều hướng nghiên cứu mới trong toán học.

Tóm lại, số vô tỉ không chỉ giúp giải quyết nhiều bài toán và phương trình mà còn là nền tảng cho nhiều khái niệm và lý thuyết toán học quan trọng. Do đó, việc hiểu đúng I là tập hợp số gì rất quan trọng.

Một số dạng toán về tập I thường gặp

Khi tìm hiểu I là tập hợp số gì, bạn có thể áp dụng tính chất của tập hợp I để giải các dạng toán có liên quan. Dưới đây là một số dạng bài tập liên quan đến số vô tỉ mà bạn có thể tham khảo:

Dạng 1: Tìm các số vô tỉ giữa hai số hữu tỉ:

Để giải quyết được dạng toán này, bạn cần hiểu đúng I là tập hợp số gì, tập hợp I gồm những số nào.

Ví dụ: Tìm số vô tỉ nằm giữa hai số 1 và 2

Cách giải: Số vô tỉ nằm giữa 1 và 2 chỉ có thể là √2 bởi 1< √2 < 2

Dạng 2: So sánh số vô tỉ và số hữu tỉ:

Ví dụ: Chứng minh π lớn hơn 3 và nhỏ hơn 4

Cách giải: Ta có: π = 3.14159

=> 3 < π < 4

Bạn có thể sử dụng một số phương pháp gần đúng hoặc giá trị ước lượng của π để chứng minh điều này một cách chặt chẽ hơn, nhưng giá trị xấp xỉ đã đủ để thấy rằng π nằm trong khoảng từ 3 đến 4.

Dạng 3: Biểu diễn số vô tỉ trên trục số:

Ví dụ: Xác định vị trí của √5 trên trục số

Cách giải:

Ta có √5 = 2.236

=> 2 < √5 < 3

Do đó √5 nằm giữa 2 và 3 trên trục số nhưng gần với 2 hơn.

Các dạng toán trên giúp chúng ta hiểu rõ hơn về tính chất và ứng dụng của số vô tỉ trong toán học. Việc làm quen I là tập hợp số gì và giải các bài toán này không chỉ giúp củng cố kiến thức về số vô tỉ mà còn phát triển tư duy logic và kỹ năng giải quyết vấn đề.

Tóm lại, nắm rõ I là tập hợp số gì, mối quan hệ giữa I với các tập hợp số khác sẽ giúp bạn dễ dàng giải được các dạng toán có liên quan đến số vô tỉ. Bên cạnh đó, việc hiểu rõ tính chất của tập hợp I cũng giúp bạn tránh được những sai sót nhỏ khi thực hiện các phép toán cộng, trừ, nhân, chia số vô tỉ.