Các thuật ngữ liên quan đến hình tròn
Các thuật ngữ hình học về đường tròn bạn cần nắm được trước khi tìm hiểu chu vi diện tích hình tròn.
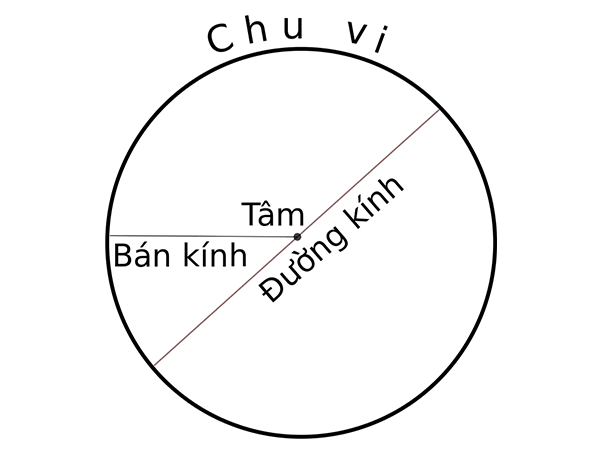
Đường tròn là một đường cong phẳng, được định nghĩa là tập hợp tất cả các điểm cách một điểm cố định (gọi là tâm) một khoảng cách bằng nhau (gọi là bán kính). Ký hiệu: O là tâm, r là bán kính.
Hình tròn là phần mặt phẳng giới hạn bởi đường tròn.
Các yếu tố cơ bản:
- Tâm (O): Điểm cố định cách đều mọi điểm trên đường tròn.
- Bán kính (r): Khoảng cách từ tâm đến bất kỳ điểm nào trên đường tròn.
- Đường kính (d): Đoạn thẳng đi qua tâm và nối hai điểm trên đường tròn, có độ dài bằng 2 lần bán kính (d = 2r).
- Chu vi (C): Độ dài của đường biên giới hạn hình tròn. Công thức tính chu vi: C = 2πr, với π ≈ 3,14159.
- Diện tích (S): Diện tích của phần mặt phẳng giới hạn bởi đường tròn. Công thức tính diện tích: S = πr².
- Số Pi (π): Tỷ số giữa chu vi và đường kính của bất kỳ đường tròn nào. π là một số vô tỷ, xấp xỉ bằng 3,14159.
- Dây cung (AB): Đoạn thẳng nối hai điểm bất kỳ trên đường tròn.
- Góc chắn cung: Góc được tạo bởi hai bán kính nối tâm đến hai đầu mút của dây cung.
- Cung tròn: Phần mặt phẳng được giới hạn bởi dây cung và hai bán kính nối tâm đến hai đầu mút của dây cung.
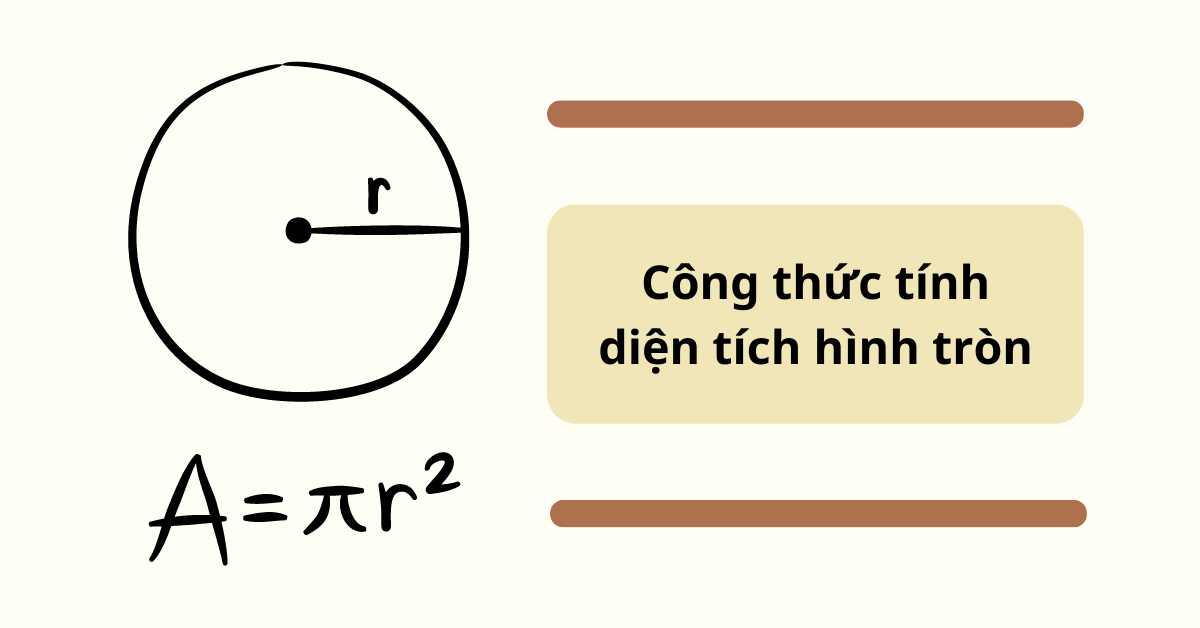
Công thức tính diện tích hình tròn
Diện tích hình tròn là diện tích của phần mặt phẳng được giới hạn bởi đường tròn. Diện tích này được tính bằng công thức sau:
S = πr²
Trong đó:
S: Diện tích hình tròn (đơn vị: mét vuông, cm vuông,...)
r: Bán kính hình tròn (đơn vị: mét, cm,...)
π: Hằng số Pi, là một số vô tỉ xấp xỉ bằng 3.14.
Công thức tính diện tích hình tròn dựa trên nguyên lý sau:
- Chia hình tròn thành nhiều hình quạt nhỏ.
- Diện tích mỗi hình quạt xấp xỉ bằng diện tích tam giác có đáy là cạnh cung và chiều cao là bán kính.
- Khi số lượng hình quạt tăng lên vô hạn, diện tích hình tròn xấp xỉ bằng tổng diện tích vô số tam giác nhỏ.
- Lấy giới hạn của biểu thức diện tích hình quạt khi số lượng hình quạt tăng lên vô hạn, ta được công thức tính diện tích hình tròn như trên.
Các dạng bài tính diện tích hình tròn
Nắm vững công thức là chìa khóa then chốt để chinh phục mọi dạng bài toán. Luyện tập nhuần nhuyễn với các dạng bài tập sau đây tạo nền tảng vững chắc cho những bài toán nâng cao hơn.
Tính diện tích hình tròn khi biết bán kính R hoặc đường kính D
Đây là dạng toán đơn giản nhất vì ta đã có sẵn công thức để áp dụng, chỉ cần thay số và tính toán là hoàn thành.
Phương pháp: Áp dụng công thức: S = r x r x 3,14
(S là diện tích hình tròn, r là bán kính hình tròn)
Ví dụ 1: Tính diện tích hình tròn có bán kính r = 5 mm.
Bài giải:
Diện tích hình tròn là: 5 × 5 × 3,14 = 78,5 (mm2)
Đáp số: 78,5 mm2
Ví dụ 2: Tính diện tích khi biết đường kính d = 1,2 dm
Phương pháp: Chúng ta vẫn áp dụng công thức S = r x r x 3,14 tuy nhiên cần linh hoạt tính bán kính theo công thức là r = d : 2 sau đó tính diện tích theo công thức.
Bài giải:
Bán kính hình tròn là: 1,2 : 2 = 0,6 (dm)
Diện tích hình tròn là: 0,6 × 0,6 × 3,14 = 1,1304 (dm2)
Đáp số: 1,1304 dm2
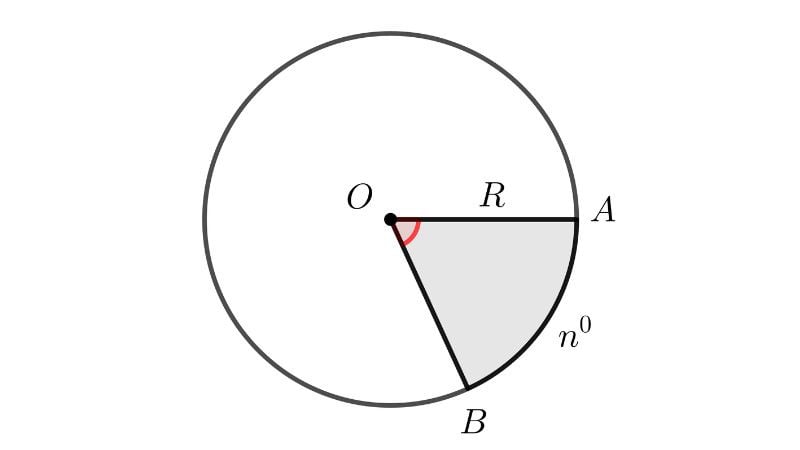
Tính diện tích hình quạt tròn
Hình quạt tròn là phần mặt phẳng được giới hạn bởi một cung tròn và hai bán kính nối từ tâm đến hai đầu mút của cung tròn. Diện tích hình quạt tròn là diện tích của phần mặt phẳng đó.
Diện tích hình quạt tròn được tính theo công thức sau:
S = (πR² * n) / 360 = l*R/2
Trong đó:
- S: Diện tích hình quạt tròn (đơn vị diện tích)
- π: Số Pi, xấp xỉ bằng 3.14159
- R: Bán kính của đường tròn (đơn vị độ dài)
- n: Số đo cung tròn (đơn vị độ)
- l là độ dài cung tròn n độ
Ví dụ 1: Biết chu vi hình tròn là 16π. Tính diện tích hình quạt tròn có số đo cung là 50° (ta sử dụng công cụ máy tính online casio fx-580vn plus)
Bài giải:
Công thức tính chu vi hình tròn là C= d * Pi
Theo đề bài 16π = d*π, do đó, đường kính d= 16 tức là r=8
Áp dụng công thức tính diện tích quạt tròn: S = (πR² * n) / 360 = l*R/2
Ta có S= (π * 8^2*50)/ 360 = 80/9π
Bài 2: Một miếng bánh Pizza có bán kính 20cm. John gọi chủ quán rằng anh ta muốn mua một miếng bánh có diện tích hình quạt tròn là 100π (cm2). Bác đầu bếp băn khoăn không biết cắt như thế nào, bạn giúp bác đầu bếp tính toán chính xác để John được miếng bánh như ý.
Bài giải:
Để xác định hình dạng và kích thước cái bánh như thế nào, ta sẽ xác định nên cắt bánh một góc bao nhiêu độ từ tâm cái bánh.
Bán kính bánh Pizza là: R = 40/2 = 20 (cm)
Diện tích hình quạt tròn do đề cho là 100π (cm2)
S = (πR² * n) / 360
Tức là n= 360 *S/ πR²= 360 * 100π/π * 20^2= 90
Nghĩa là nếu ta cắt cái bánh từ tâm tạo thành góc vuông thì sẽ đúng yêu cầu của John.
So sánh diện tích hình tròn
Bài toán so sánh diện tích hai hình tròn thường yêu cầu ta thực hiện các bước sau:
Bước 1: Quy đổi đơn vị nếu cần vì phải đảm bảo hai hình tròn có cùng đơn vị diện tích trước khi so sánh.
Bước 2: Áp dụng công thức tính diện tích hình tròn: S = πr², trong đó r là bán kính hình tròn. Thay giá trị bán kính/ đường kính đã cho vào công thức để tính diện tích của mỗi hình tròn.
Bước 3: Sử dụng các phép so sánh toán học (>, <, =) để so sánh diện tích hai hình tròn đã tính được.
Ví dụ: So sánh diện tích hai hình tròn sau:
Hình tròn S1 có diện tích là 1000 mm2
Hình tròn S2 có diện tích là 12cm2
Giải: Ta thực hiện quy đổi diện tích của S1 sang cm2: 1000mm2 = 10cm2
=> S2 > S1
Vậy hình tròn S2 có diện tích lớn hơn hình tròn S1.
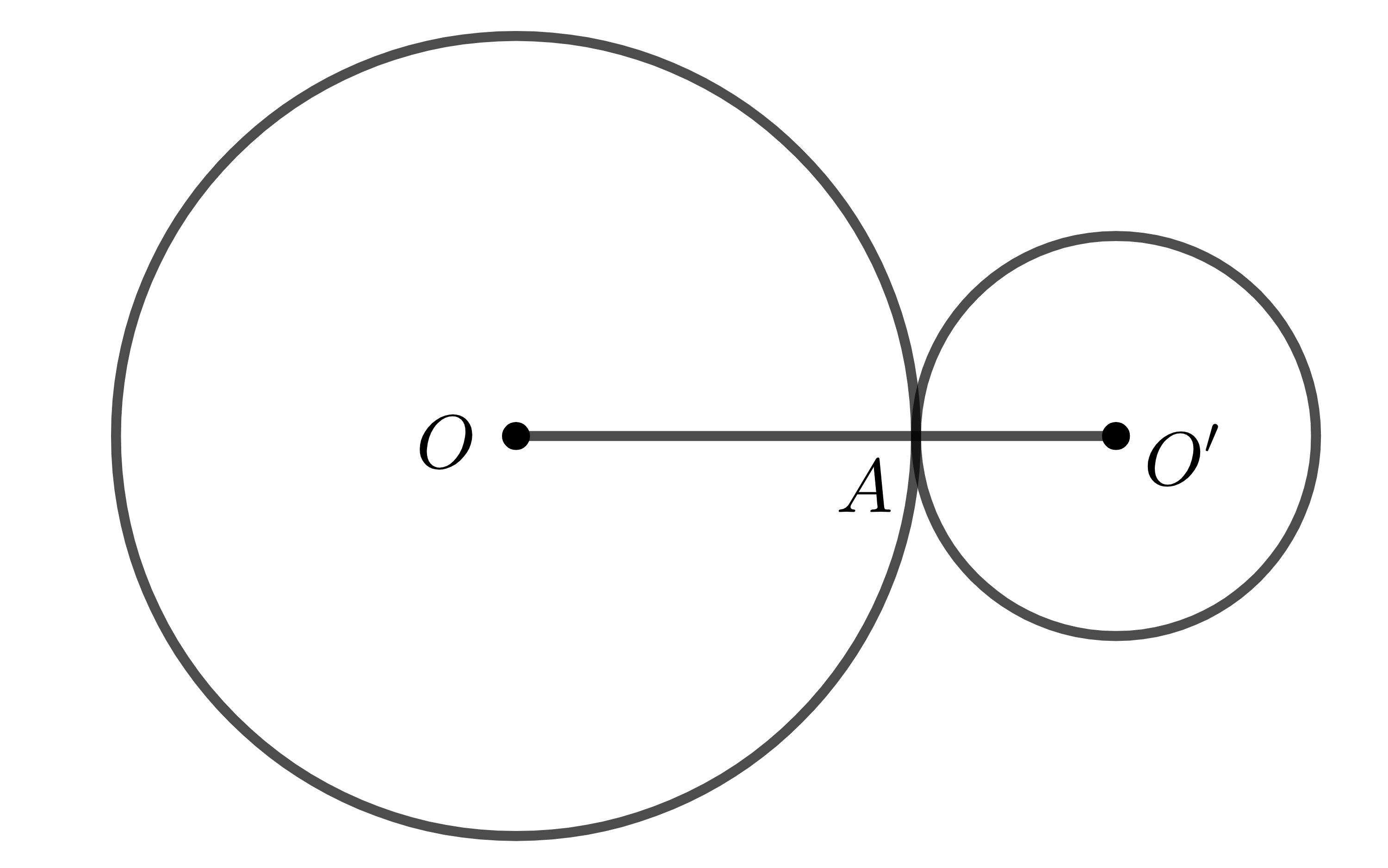
Tính diện tích vành khăn
Hình vành khăn là phần hình tròn giống phần rìa nằm giữa hai đường tròn đồng tâm. Tính diện tích hình vành khăn là một dạng bài tập hình học khá phổ biến, đòi hỏi sự hiểu rõ về công thức khi muốn tính diện tích hình tròn và khả năng áp dụng linh hoạt.
Diện tích hình vành khăn được tính theo công thức sau:
S = π[(R₁)² - (R₂)²]
Trong đó:
- S: Diện tích hình vành khăn (đơn vị diện tích)
- π: Số Pi, xấp xỉ bằng 3.14
- R₁: Bán kính của đường tròn lớn (đơn vị độ dài)
- R₂: Bán kính của đường tròn nhỏ (đơn vị độ dài)
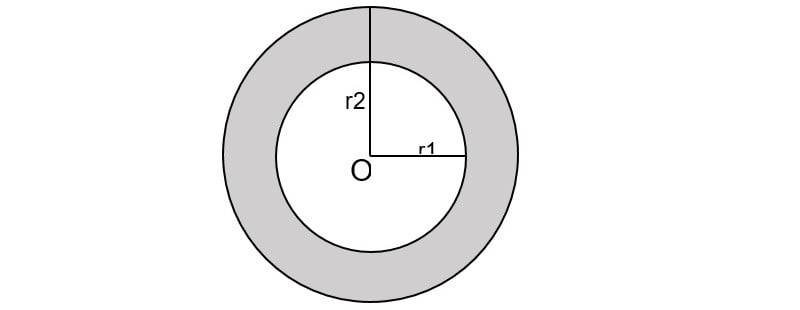
Lưu ý: Cần đảm bảo đơn vị đo của R₁ và R₂ là đồng nhất trước khi áp dụng công thức.
Ví dụ 1: Tính diện tích hình vành khăn có bán kính đường tròn lớn R₁ = 5cm và bán kính đường tròn nhỏ R₂ = 3cm:
S = π(5² - 3²) ≈ 12.57 cm²
Ngoài ra bạn có thể tìm diện tích của 2 hình tròn rồi tìm hiệu của chúng.
Ví dụ: Cho 2 hình tròn đồng tâm khác bán kính lồng vào nhau, tính phần diện tích rìa ngoài. Biết, đường tròn nhỏ bên trong có bán kính 10mm, đường tròn lớn bên ngoài bán kính là 2cm.
Bài giải: Diện tích hình tròn nhỏ: S1 = πR1^2 = 3,14.10^2 = 314 mm2
Diện tích hình tròn lớn: S2 = πR^2 = 3,14.20^2 = 1256 mm2
Diện tích phần rìa là: S = S2 – S1 = 1256 – 314 = 942 mm2
Tính diện tích hình bất kỳ có chứa 1 phần diện tích hình tròn
Dạng bài tập tính diện tích hình bất kỳ có chứa 1 phần diện tích hình tròn là một thử thách nâng cao trong môn toán học. Để giải quyết dạng bài toán này, bạn cần trang bị kiến thức về công thức tính diện tích của các hình cơ bản (hình vuông, hình chữ nhật, tam giác, hình thang,...) và khả năng phân chia, tách ghép hình vẽ một cách linh hoạt.
Ví dụ: Tính diện tích của toàn bộ hình trên bao gồm diện tích của hình chữ nhật kích thước 10mm và 7mm, diện tích của 2 nửa hình tròn bán kính r = 7mm.
Diện tích hình chữ nhật là 10 x 7 x 2 = 140mm2
Diện tích hai nửa hình tròn cùng bán kính: S2 = πR2 = 3,14 x 7^2 = 153,86 cm2
=> Diện tích toàn bộ hình: S 140 + 153,86 = 293,86 mm2
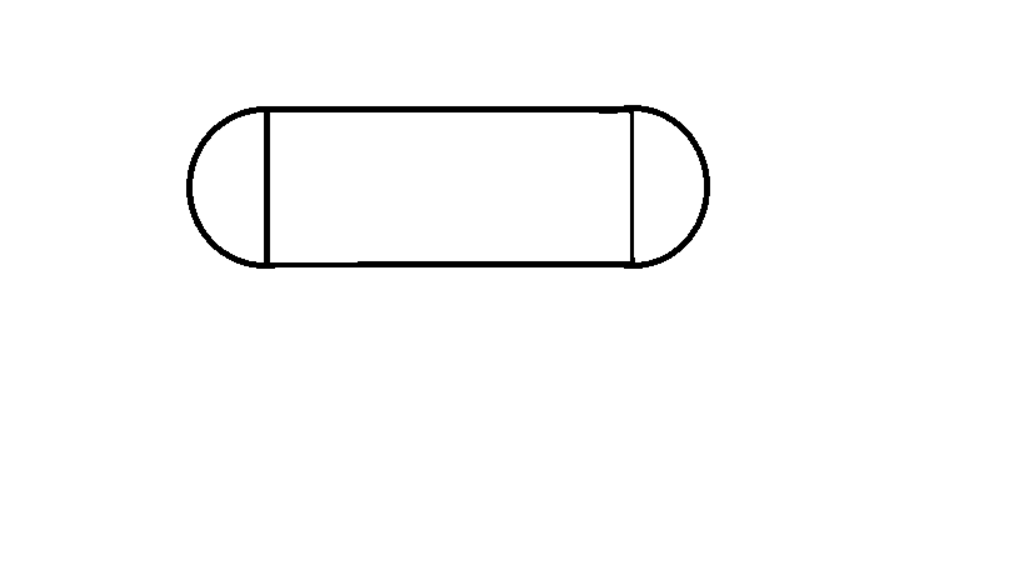
Cho diện tích của hình tròn, tính chu vi của hình tròn
Bước 1: Tìm bán kính (r) bằng cách áp dụng công thức r = √(S / π) để tính bán kính r khi biết diện tích S.
Bước 2: Tìm chu vi (C): Thay giá trị r đã tính được vào công thức C = 2πr. Thực hiện tính toán để tìm chu vi C.
Bài toán tính diện tích hình tròn từ đường kính (Nâng cao)
Đây cũng là dạng bài tập toán về hình tròn dạng nâng cao hơn nhưng tùy thuộc vào điều kiện đã cho để tìm được bán kính/ đường kính rồi mới tính toán được S.
Ví dụ: Tính diện tích hình tròn biết nếu tăng đường kính đường tròn lên 30% thì diện tích của nó tăng thêm 20 m2 nữa.
Bài giải:
Nếu tăng đường kính hình tròn tăng thêm 30% thì bán kính cũng tăng thêm 30%.
Số % diện tích được tăng thêm sẽ là: (130%)2 – (100%)2 = 69%
Do đó, diện tích hình tròn ban đầu: 20×100/69 = 29,956 mm2
Ví dụ về bài toán hình tròn trong đề thi
Bài 1: Tính bán kính đường tròn có chu vi là 100 cm
Bài 2: Tính đường kính hình tròn cho chu vi l là 21,98cm
Bài 2: Một bảng hướng dẫn giao thông hình tròn có đường kính 40cm. Diện tích phần mũi tên trong biển báo bằng 1/4 diện tích cả biển báo. Tính diện tích còn lại của biển báo đó.
Bài 3: Nhà em có đào 1 cái giếng, miệng giếng có hình tròn có bán kính 0,8 m. Xung quanh miệng giếng được xây thành giếng rộng 0,3m. Tính diện tích của thành giếng.
Bài 4: Trong sân trường em, nhà trường có trồng 2 bồn hoa hình tròn. Bồn hoa cúc có bán kính 20dm còn bồn trồng hoa hồng có chu vi là 9,42 m. Hỏi bồn hoa nào có diện tích nhỏ hơn và lớn hơn với khoảng cách diện tích là bao nhiêu?
Bài 5: Tìm chu vi và diện tích hình tròn có: d = 5,2 mm ; d = 1,2 mm ; d = ⅗ dm.
Bài 6: Một bảng chỉ dẫn đường hình tròn có đường kính 5 dm.
a. Tính diện tích bảng này bằng đơn vị mét vuông?
b. Người ta đem sơn hai mặt của tấm bảng đó, mỗi mét vuông tốn chi phí 7 ngàn đồng. Hỏi nếu sơn kín 2 mặt tấm bảng đó sẽ tốn chi phí bao nhiêu tiền?
Bài 7: Tính diện tích phần viền bên ngoài của 2 hình tròn lồng vào nhau biết 2 hình tròn có cùng tâm và có bán kính dài lần lượt là 0,8 m và 0,5m.
Bằng cách rèn luyện tư duy logic, sáng tạo và vận dụng kiến thức phù hợp, học sinh sẽ tự tin giải quyết mọi dạng bài toán một cách chính xác và hiệu quả. Hãy biến việc học toán trở nên thú vị và bổ ích bằng cách biến những bài toán về diện tích hình tròn thành những thử thách chinh phục đầy hấp dẫn.
