Dấu hiệu nhận biết hình thang
Dấu hiệu nhận biết hình thang: Một tứ giác có hai cạnh đối song song với nhau được gọi là hình thang. Hai cạnh đối song song này là hai đáy của hình thang, gồm đáy lớn (cạnh dài) và đáy bé (cạnh ngắn hơn).
Dấu hiệu nhận biết hình thang cân:
- Nếu trong hình thang, hai góc kề cạnh đáy bằng nhau thì đó chính là hình thang cân.
- Nếu hai đường chéo của hình thang bằng nhau thì hình thang đó là hình thang cân.
- Hình thang có trục đối xứng của hai đáy trùng nhau thì đó là hình thang cân.
- Nếu hai cạnh bên của hình thang bằng nhau và chúng không song song thì hình thang đó là hình thang cân.
- Một hình thang nội tiếp đường tròn nghĩa là hình thang cân.
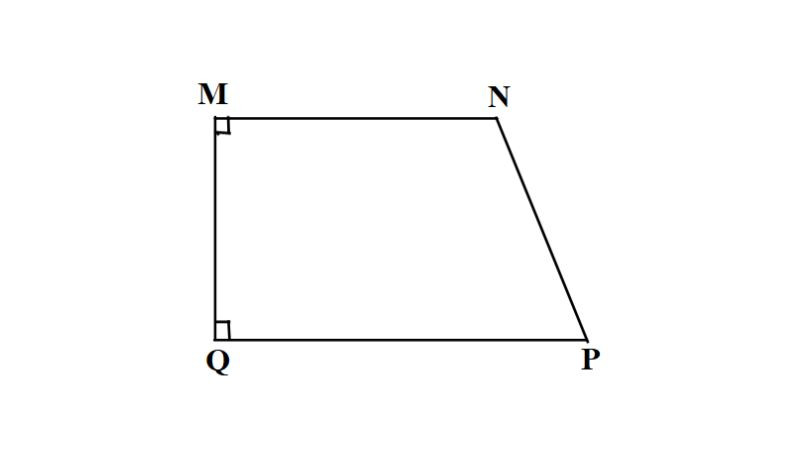
Dấu hiệu nhận biết hình thang vuông: Hình thang có một góc vuông là hình thang vuông.
Hướng dẫn cách tính diện tích hình thang
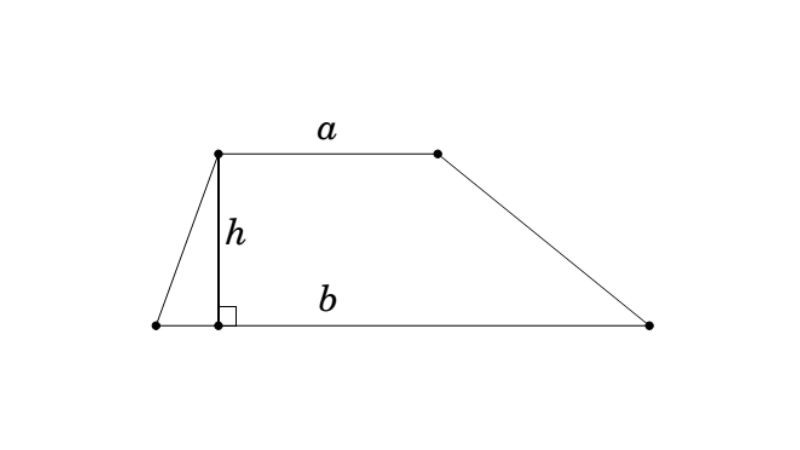
Để tính diện tích hình thang, bạn sẽ lấy tổng chiều dài của hai cạnh đáy, sau đó nhân với chiều cao rồi chia cho 2. Khi tính diện tích, bạn cần đảm bảo tất cả các số đo đều cùng một đơn vị (nếu chiều dài một cạnh đáy là cm thì chiều dài cạnh đáy còn lại cũng phải là cm).
Ngoài ra, trong từng trường hợp riêng biệt, bạn có thể áp dụng công thức tính diện tích hình thang như sau:
Cách tính diện tích hình thang thường
Diện tích hình thang thường (S) được tính bằng công thức sau: S = (a + b) * h / 2
Trong đó:
- S: Diện tích hình thang (đơn vị đo: cm², m², inch²,...)
- a: Độ dài cạnh đáy nhỏ (đơn vị đo: cm, m, inch,...)
- b: Độ dài cạnh đáy lớn (đơn vị đo: cm, m, inch,...)
- h: Chiều cao của hình thang (đơn vị đo: cm, m, inch,...)
Ví dụ:
Cho hình thang ABCD với độ dài hai đáy lần lượt là AD = 6 cm, BC = 10 cm và chiều cao hình thang là DH = 8 cm. Diện tích hình thang trên được tính như sau kết hợp công cụ máy tính 580 online:
S = (AD + BC) * DH / 2 = (6 + 10) * 8 / 2 = 56 cm²
Đáp số: Diện tích hình thang ABCD là 56 cm².

Diện tích hình thang cân
Hình thang cân là tứ giác có hai cạnh đáy song song và hai góc kề một đáy bằng nhau. Để tính diện tích của hình thang cân, chúng ta sử dụng công thức tương tự như công thức tính diện tích hình thang thường. Đó là: S = (a + b) * h / 2
Trong đó:
- S: Diện tích hình thang (đơn vị đo: cm², m², inch²,...)
- a: Độ dài cạnh đáy nhỏ (đơn vị đo: cm, m, inch,...)
- b: Độ dài cạnh đáy lớn (đơn vị đo: cm, m, inch,...)
- h: Chiều cao của hình thang (đơn vị đo: cm, m, inch,...)
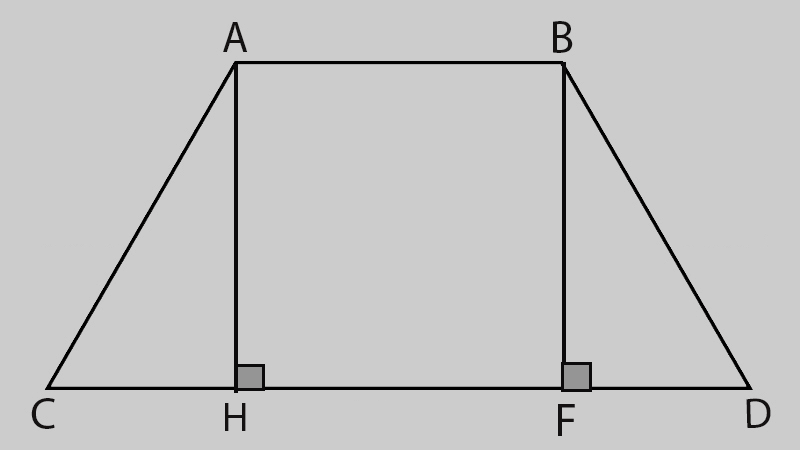
Do đây là hình đặc biệt nên bạn hoàn toàn có thể sử dụng cách chia nhỏ hình thang thành hai hình tam giác và 1 hình chữ nhật như hình minh họa để tính diện tích từng phần rồi cộng lại với nhau sẽ cho ra kết quả cuối là diện tích hình thang cân cần tìm.
Tính diện tích hình thang vuông
Hình thang vuông là một loại hình thang đặc biệt với một góc vuông (90 độ). Hình thang này có chiều cao bằng cạnh bên góc vuông. Về bản chất, công thức tính diện tích hình thang vuông cũng giống như công thức tính diện tích hình thang thường là: S = (a + b) * h / 2
Trong đó:
- S: Diện tích hình thang vuông (đơn vị đo: cm², m², inch²,...)
- a: Độ dài cạnh đáy góc vuông (đơn vị đo: cm, m, inch,...)
- b: Độ dài cạnh đáy song song với cạnh góc vuông (đơn vị đo: cm, m, inch,...)
- h: Chiều cao của hình thang vuông (đơn vị đo: cm, m, inch,...)
Ví dụ: Cho hình thang vuông ABCD với độ dài cạnh đáy góc vuông AB = 5 cm, độ dài cạnh đáy song song với cạnh góc vuông CD = 8 cm và chiều cao hình thang là AD = 6 cm. Diện tích hình thang này được tính như sau:
S = (AD + BC) * DH / 2 = (5 + 8) * 6 / 2 = 39 cm2
Vậy diện tích hình thang ABCD là 39 cm2
Ta có thể tính diện tích hình thang vuông bằng cách chia hình thang vuông thành hai phần: một tam giác vuông và một hình chữ nhật. Diện tích của tam giác vuông bằng một nửa tích hai cạnh góc vuông và diện tích của hình chữ nhật bằng tích của chiều dài và chiều rộng. Sau đó, ta cộng diện tích của tam giác vuông và diện tích của hình chữ nhật để được diện tích của hình thang vuông.
Ví dụ:
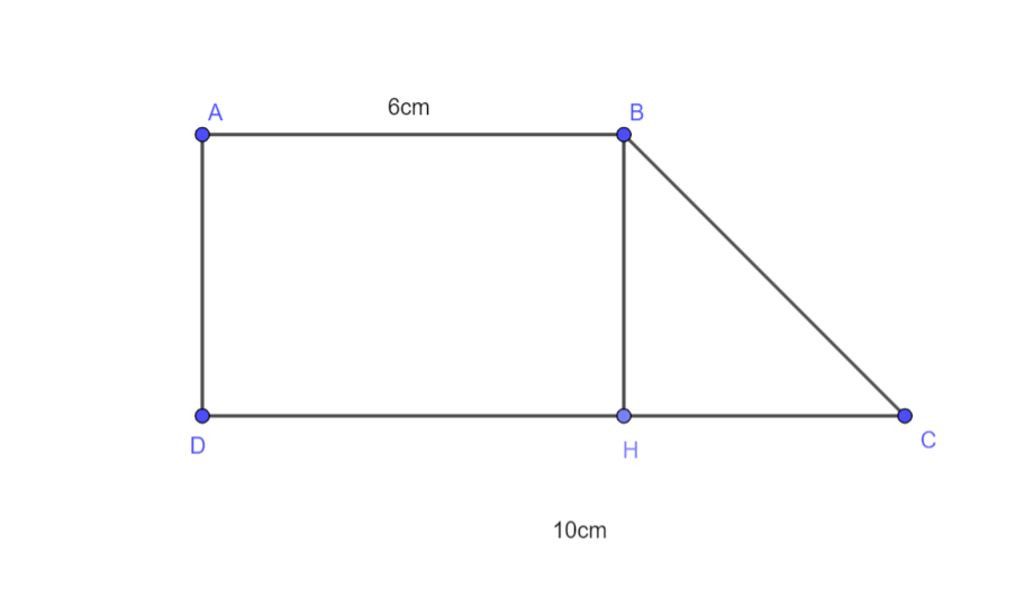
Cho hình thang vuông ABCD với độ dài cạnh đáy góc vuông AB = 5 cm, độ dài cạnh đáy song song với cạnh góc vuông CD = 8cm và chiều cao hình thang là AD = 6 cm. Diện tích hình thang ABCD được tính như sau:
Ta kẻ BH song song với AD, BH= AD và AB=DH
Diện tích tam giác vuông BHC = (1/2) * BH*HC = (1/2) * (CD-AB)* 6 = 9 cm2
Diện tích hình chữ nhật ABHD = 5 * 6 = 30 cm2
Diện tích hình thang vuông ABCD = Diện tích tam giác vuông BHC + Diện tích hình chữ nhật ABHD 39 cm2
Công thức tính chiều cao, đáy lớn, đáy nhỏ của hình thang
Để tính chiều cao, đáy lớn, đáy nhỏ của hình thang thông qua diện tích chúng ta đều cần xuất phát từ công thức gốc đó là S = (a + b) * h / 2.
Giả sử bạn đã biết diện tích (S) và độ dài hai cạnh đáy (a, b) của hình thang. Lúc này, chiều cao (h) của hình thang được tính theo công thức sau: h = (S x 2) / (a + b)
Trong đó:
h: Chiều cao của hình thang (đơn vị đo: cm, m, inch,...)
S: Diện tích của hình thang (đơn vị đo: cm², m², inch²,...)
a: Độ dài cạnh đáy lớn (đơn vị đo: cm, m, inch,...)
b: Độ dài cạnh đáy nhỏ (đơn vị đo: cm, m, inch,...)
Ví dụ: Cho hình thang ABCD có diện tích S = 50 cm², độ dài cạnh đáy lớn a = 10 cm và độ dài cạnh đáy nhỏ b = 8 cm. Chiều cao h của hình thang này được tính như sau:
h = (50 x 2) / (10 + 8) = 50 / 18 = 2.78 cm
Vậy chiều cao của hình thang ABCD là 2.78 cm.
Nếu biết diện tích S và chiều cao h, ta có thể tính độ dài của đáy theo công thức sau:
a = (2 x S) / h - b và b = (2 x S) / h - a hoặc a+b = (2 x S) / h
Các dạng bài tập về diện tích hình thang
Hình thang là một tứ giác quen thuộc trong toán học, xuất hiện trong nhiều ứng dụng thực tế. Việc tính toán diện tích hình thang tưởng chừng đơn giản nhưng lại có rất nhiều dạng bài tập đa dạng, đòi hỏi sự linh hoạt và tư duy logic của người học.
Tính diện tích khi biết a, b và h
Đây là dạng toán tương đối đơn giản vì đề đã cho gần hết các dữ kiện.
Bước 1: Tính tổng 2 cạnh đáy
Bước 2: Tính chiều cao của hình thang
Bạn chỉ cần vẽ đường thẳng từ trên xuống dưới sao cho đường thẳng đó vuông góc với cạnh đáy. Nếu đề không cho sẵn thông số, bạn cần linh hoạt tính toán từ những dữ kiện khác để tìm ra h.
Lưu ý: Trong hình thang vuông sẽ có một cạnh bên là chiều cao nếu nó vuông góc với 2 cạnh đáy.
Bước 3: Áp dụng công thức
Đừng quên đổi các số liệu về cùng một đơn vị đo trước khi đưa vào công thức tính toán để phép tính chính xác. Ở bước này, bạn chỉ cần lấy chiều cao nhân với tổng 2 đáy của hình thang rồi chia cho 2 là ra kết quả cuối cùng.

Tính diện tích hình thang khi biết độ dài 4 cạnh
Cần lưu ý, dạng bài này chỉ có thể áp dụng cho hình thang cân. Khi bạn chỉ biết độ dài cạnh bên, bạn có thể áp dụng công thức tính diện tích hình thang theo cách khác với các bước cơ bản sau:
Bước 1: Chia nhỏ hình thang thành 2 tam giác vuông và 1 hình chữ nhật
Đầu tiên, bạn kẻ thêm 2 đường thẳng, mỗi đường thẳng bắt nguồn từ 1 góc của cạnh đáy nhỏ nối với cạnh lớn bên dưới sao cho đường thẳng đó vuông góc với đáy. Khi đó, hình sẽ bao gồm 1 hình chữ nhật, 2 tam giác vuông có cạnh huyền bằng nhau.
Bước 2: Tìm độ dài cạnh đáy tam giác
Lấy đáy lớn trừ đáy nhỏ, sau đó chia 2 sẽ tìm ra độ dài của đáy hình tam giác vuông.
Giả sử: Một hình thang có cạnh đáy trên 7cm, cạnh đáy dưới 15cm, vậy cạnh đáy hình tam giác = (15 – 7) / 2 = 4 (cm).
Bước 3: Sử dụng công thức Pytago để tính ra độ dài cạnh góc vuông còn lại rồi áp dụng cho công thức tính diện tích hình thang ở bước trên.
Ví dụ: Sau khi tính được cạnh đáy của tam giác vuông là 4cm mà đề bài cho cạnh huyền = 5cm, ta sẽ tìm được cạnh góc vuông còn lại (chính bằng chiều cao của hình thang) là: 25 – 16 = 9 = (3)^2 (cm).
Vậy, chiều cao hình thang = 3cm.
Bước 4: Áp dụng công thức tính
S = (7 + 15) x 3/2 =33 (cm2)
Một số bài toán nâng cao luyện tập
Bài 1: Một hình thang có đáy nhỏ dài 8cm, đáy lớn dài 18cm được chia thành hai hình thang có đáy chung dài 14cm. Hãy so sánh diện tích của 2 hình thang có đáy chung nói trên.
Bài 2: Cho hình thang MHIK, hai đáy MH và IK. Hai đường chéo MI và KH cắt nhau tại O. Hãy tìm các tam giác có cùng diện tích với nhau.
Bài 3: Cho hình thang ABCD, hai đáy AD và BC, hai đường chéo AC và BD giao nhau tại K. Tính diện tích các tam giác KAB, KBC, KCD, KDA biết rằng AD = 20cm; BC = 10cm và đường cao của hình thang bằng 12cm.
Lưu ý khi làm bài tập tính diện tích hình thang
Khi giải bài tập tính diện tích hình thang, việc ghi nhớ và áp dụng đúng công thức cùng với các lưu ý quan trọng sẽ giúp học sinh giải quyết đề bài một cách chính xác và hiệu quả hơn:
- Đảm bảo hiểu rõ các thông số trong bài tập, bao gồm độ dài của hai cạnh đáy và chiều cao của hình thang. Xác định chính xác các thông số này là bước đầu tiên và quan trọng nhất để tính diện tích.
- Chú ý các đơn vị đo lường cần sử dụng đồng nhất trong toàn bộ bài tập. Việc không đồng nhất về đơn vị có thể dẫn đến sai sót trong tính toán và kết quả không chính xác.
- Luôn kiểm tra lại kết quả sau khi tính toán để đảm bảo tính chính xác và tránh sai sót. Việc kiểm tra có thể bao gồm việc so sánh với kết quả ước tính ban đầu hoặc tính toán lại các bước quan trọng.
- Hiểu về các dạng bài tập khác nhau: Làm quen với các dạng bài tập đa dạng, từ các bài tập cơ bản đến những bài toán phức tạp hơn. Điều này sẽ giúp học sinh hiểu sâu hơn về các phương pháp giải toán và áp dụng linh hoạt trong nhiều tình huống.
Qua việc làm các bài tập diện tích hình thang, học sinh có thể rèn luyện khả năng phân tích, logic và tính toán. Đồng thời, việc hiểu biết và áp dụng đúng các công thức khi giải quyết các bài toán sẽ giúp bạn phát triển kỹ năng toán học một cách toàn diện và hiệu quả.
