Tìm hiểu sơ lược về hình tam giác
Hình tam giác là một trong những hình học cơ bản và quan trọng nhất mà học sinh cần nắm vững trong quá trình học toán ở các cấp độ.
Hình tam giác là gì?
Hình tam giác là một hình 2 chiều với ba đỉnh là ba điểm không nằm trên cùng một đường thẳng và ba cạnh là ba đoạn thẳng kết nối các đỉnh này lại với nhau. Ngoài ra, tam giác còn là đa giác có số cạnh ít nhất, đồng thời cũng là một đa giác đơn và lồi, với các góc trong luôn nhỏ hơn 180°.
Phân loại hình tam giác
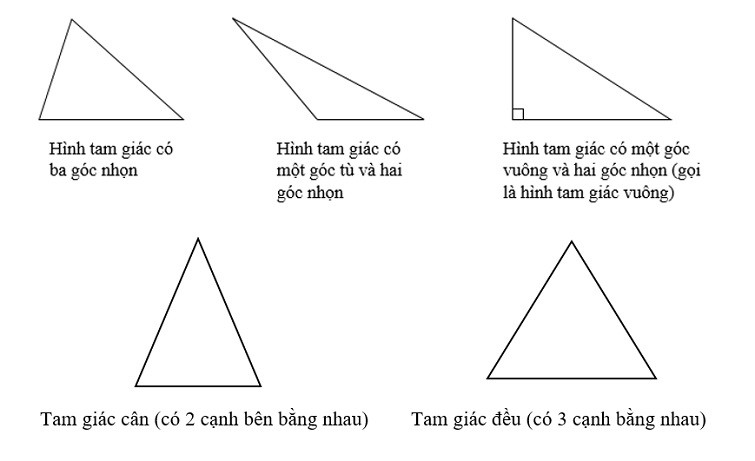
Tam giác có thể được phân loại dựa trên độ dài các cạnh và số đo các góc của nó. Dưới đây là các loại tam giác chính:
Dựa trên độ dài các cạnh:
- Tam giác đều: Cả ba cạnh đều bằng nhau và cả ba góc đều bằng 60°.
- Tam giác cân: Có độ dài hai cạnh và hai góc đối diện với hai cạnh này bằng nhau.
- Tam giác thường: Cả ba cạnh có độ dài khác nhau và ba góc cũng khác nhau.
Dựa trên số đo các góc:
- Tam giác nhọn: Tam giác có các góc nhỏ hơn 90°.
- Tam giác vuông: Có một góc bằng 90°. Cạnh đối diện góc vuông gọi là cạnh huyền, hai cạnh còn lại gọi là cạnh góc vuông.
- Tam giác tù: Có một góc lớn hơn 90°.
Mỗi tam giác có thể thuộc vào cả hai nhóm phân loại này. Ví dụ, một tam giác vuông có thể là tam giác cân nếu hai cạnh góc vuông bằng nhau.
Công thức tính diện tích hình tam giác
Hiện nay, có rất nhiều công thức tính diện tích hình tam giác khác nhau, mỗi công thức sẽ phù hợp với các giả thiết khác nhau của đề bài. Bạn nên dựa vào các dữ kiện mà đề bài cung cấp để chọn công thức phù hợp nhất cho từng trường hợp.
Cách tính diện tích của một hình tam giác bất kỳ
Để tính diện tích của một tam giác thường (tam giác không đặc biệt), bạn có thể sử dụng công thức sau:
Diện tích tam giác = (1/2) * cạnh a * cạnh b * sin(C)
Trong đó:
- a, b là độ dài hai cạnh của hình tam giác
- C là góc nằm giữa hai cạnh a và b
Ví dụ: Nếu một tam giác có cạnh a = 5 đơn vị, cạnh b = 6 đơn vị và góc C = 60 độ, thì diện tích của tam giác sẽ là:
Diện tích = (1/2) * 5 * 6 * sin(60°) = 15 * sin(60°) = 15 * √3/2 = 12.9 (đơn vị vuông)
Vậy diện tích của tam giác này là 12.9 (đơn vị vuông).
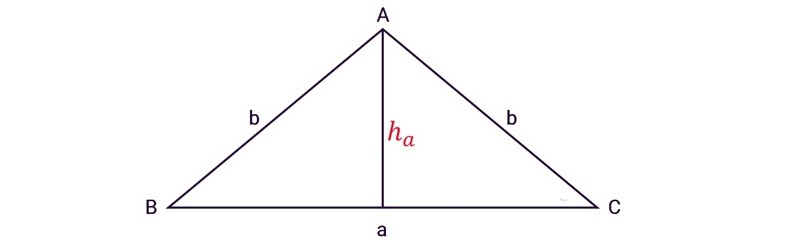
Cách tính diện tích của hình tam giác cân
Tam giác cân có đặc điểm là hai cạnh bên bằng nhau, cạnh còn lại là cạnh đáy. Để tính diện tích tam giác cân, ta sử dụng công thức: diện tích bằng một nửa chiều cao nhân với cạnh đáy tương ứng.
S = (1/2) * chiều cao * cạnh đáy
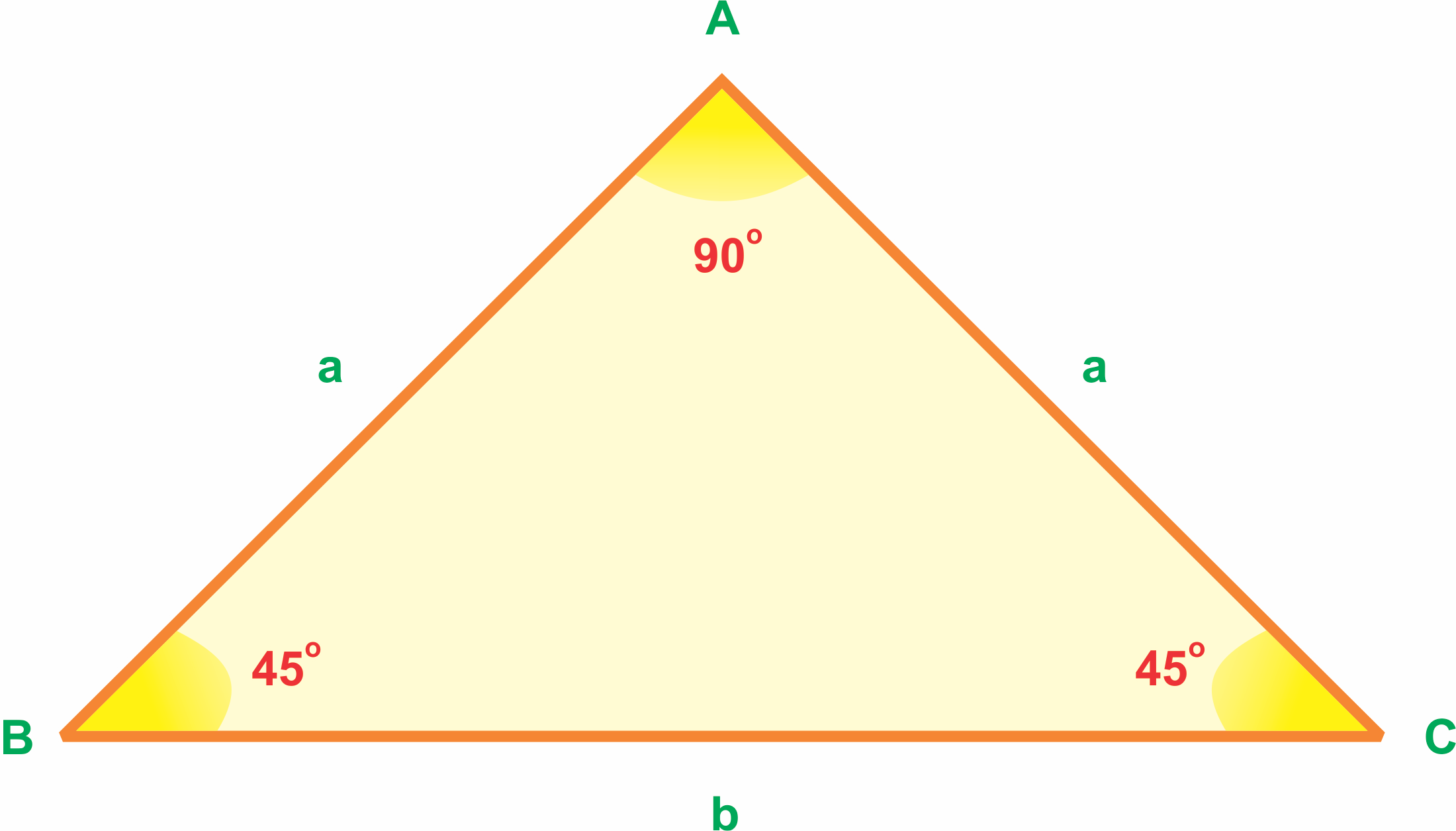
Ngoài ra, tam giác cân có một trường hợp đặc biệt gọi là tam giác vuông cân. Trong tam giác này, hai cạnh góc vuông bằng nhau. Khi đó, muốn tính diện tích tam giác này ta chỉ cần sử dụng công thức: S = (1/2) * a^2, với a là độ dài cạnh góc vuông.
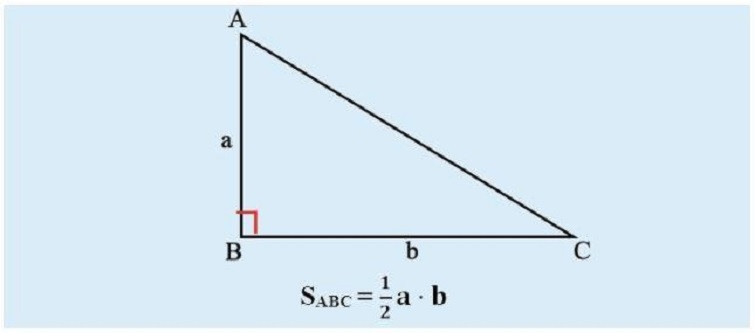
Cách tính diện tích hình tam giác vuông
Tam giác vuông là một dạng đặc biệt của tam giác thường, trong đó một trong các góc của tam giác là 90 độ.
Với một tam giác vuông, công thức tính diện tích trở nên đơn giản hơn so với trường hợp tam giác thường. Do giá trị của sin (90°) luôn bằng 1 nên ta có thể bỏ đi yếu tố này trong công thức chung. Chỉ cần biết độ dài của hai cạnh góc vuông, ta có thể ngay lập tức tính ra diện tích của tam giác.
Cụ thể: S = (1/2) * a * b,
Trong đó a, b là độ dài của hai cạnh góc vuông.
Cách tính diện tích hình tam giác đều
Tam giác đều là một loại tam giác đặc biệt với ba cạnh có độ dài bằng nhau và ba góc trong đều bằng 60 độ. Diện tích của tam giác đều có thể được tính bằng công thức đơn giản như sau: S = (1/2) * A^2 * sin(60°).
Trong đó, A là độ dài của mỗi cạnh tam giác.
Khi thay giá trị của sin (60°), ta có thể viết lại công thức này thành dựa trên máy tính online:
S = (A^2 * √3) / 4
Một số dạng bài toán về tính diện tích hình tam giác
Tính diện tích tam giác là một trong những bài toán căn bản và quen thuộc trong toán học. Từ hình học cơ bản đến các ứng dụng phức tạp, việc tính toán diện tích tam giác đóng vai trò quan trọng trong nhiều lĩnh vực. Có rất nhiều công thức và dạng toán khác nhau liên quan đến việc tính diện tích tam giác, chúng ta cùng tìm hiểu trong nội dung dưới đây:
Diện tích hình tam giác trong hệ trục tọa độ Oxyz
Ngoài các công thức tính diện tích tam giác trên mặt phẳng thông thường, khi làm việc trong hệ tọa độ Oxyz, chúng ta cũng cần nắm rõ cách tính diện tích tam giác.
Công thức tính diện tích tam giác trong không gian 3 chiều là:
S_ABC = 1/2 * [AB;AC]
Trong đó, [AB;AC] được tính như sau:
Gọi điểm A có toạ độ là (a1, b1, c1), điểm B có toạ độ là (a2, b2, c2) và điểm C có toạ độ là (a3, b3, c3). Ta có:
AB = (a2-a1; b2-b1; c2-c1)
AC = (a3-a1; b3-b1; c3-c1)
Khi đó, vectơ [AB;AC] = [(b2 - b1)(c3 - c1) - (c2 - c1)(b3 - b1); (c2 - c1)(a3 - a1) - (a2 - a1)(c3 - c1); (a2 - a1)(b3 - b1) - (b2 - b1)(a3 - a1)]
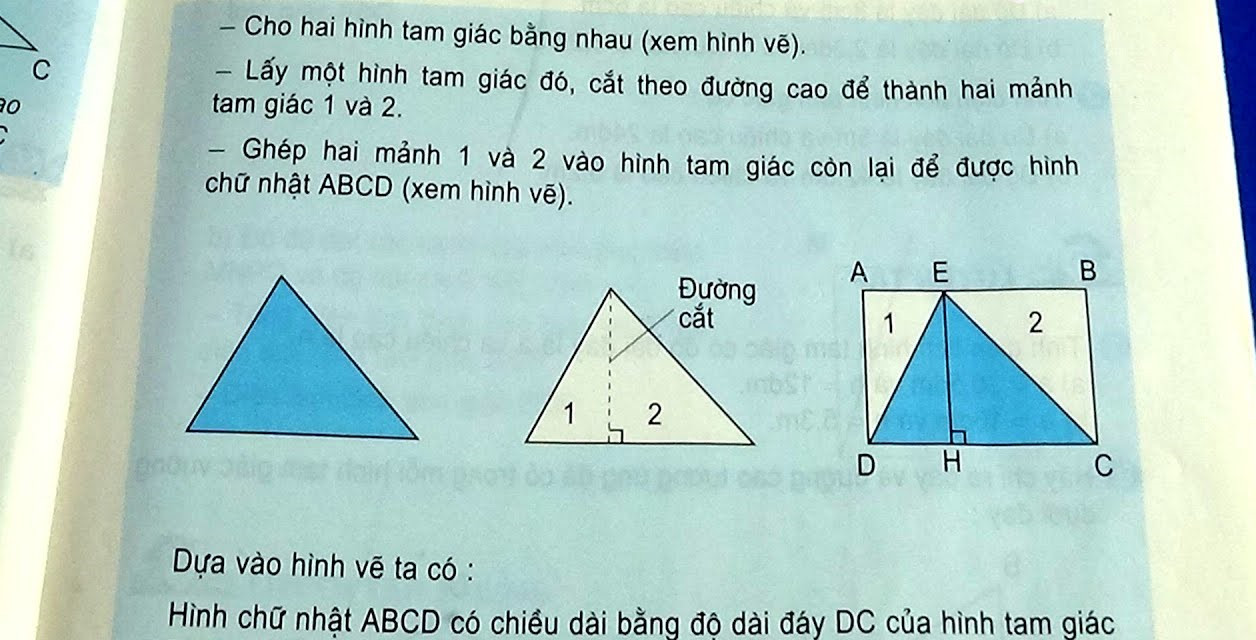
Diện tích của hình tam giác khi cho trước độ dài cạnh đáy và chiều cao
Khi đề bài cho trước độ dài cạnh đáy và đường cao, diện tích hình tam giác lúc này được tính bằng một phần hai tích của chiều cao và cạnh đáy tương ứng. Đây là công thức cơ bản và phổ biến nhất để tính diện tích tam giác.
S = ½ x Chiều cao x Độ dài cạnh đáy
Diện tích hình tam giác khi biết độ dài 2 cạnh và góc xen giữa
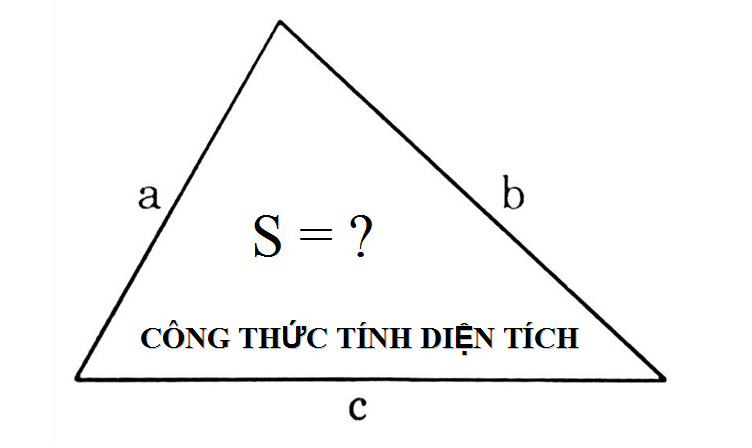
Nếu giả thiết cung cấp độ dài của hai cạnh và góc xen giữa chúng, ta có thể sử dụng công thức sau để tính diện tích tam giác: diện tích bằng một nửa tích của hai cạnh nhân với sin của góc xen giữa hai cạnh đó.
S = 1/2 x a x b x Sin(C)
Diện tích hình tam giác khi biết bán kính và chu vi đường tròn nội tiếp
Trong trường hợp giả thiết cung cấp chu vi của tam giác và bán kính của đường tròn nội tiếp tam giác, ta có thể tính diện tích của tam giác bằng cách sử dụng một công thức đơn giản. Ta chỉ cần lấy nửa chu vi của tam giác, ký hiệu là p, nhân với bán kính của đường tròn nội tiếp, ký hiệu là r , kết quả thu được chính là diện tích của tam giác cần tính.
S = p * r / 2
Diện tích hình tam giác khi biết độ dài 3 cạnh và bán kính của đường tròn ngoại tiếp
Ngoài các công thức tính diện tích tam giác được đề cập trước đó, còn có một số cách tính khác mà chúng ta cần lưu ý khi giải các bài tập liên quan.
Một cách tính diện tích tam giác khác là sử dụng độ dài của 3 cạnh và bán kính của đường tròn ngoại tiếp. Cụ thể, công thức tính sẽ là:
S = (a*b*c) / (4R)
Trong đó a, b, c lần lượt là độ dài 3 cạnh của hình tam giác, R là bán kính của đường tròn ngoại tiếp.
Một công thức khác để tính diện tích tam giác là công thức Hê-rông:
S = √(p * (p - a) * (p - b) * (p - c))
Trong đó: p là nửa chu vi của tam giác và a, b, c lần lượt là độ dài 3 cạnh.
Một số bài tập áp dụng cách tính diện tích hình tam giác
Tiếp theo, bài viết sẽ cung cấp cho bạn một số ví dụ về bài toán tính diện tích tam giác, đồng thời minh họa cách áp dụng và tính toán dựa trên các công thức thực tế. Những ví dụ này sẽ giúp bạn hình dung và hiểu rõ hơn về cách tính diện tích hình tam giác.
Bài tập 1:
Một hình tam giác MNP có độ dài các cạnh là a = 6 cm, b = 8 cm và c = 10 cm. Hãy tính diện tích của tam giác MNP.
Lời giải:
Để tính diện tích của tam giác ABC, ta sử dụng công thức Hê-rông:
S = √(p * (p - a) * (p - b) * (p - c))
Trong đó:
- a = 6 cm, b = 8 cm, c = 10 cm là độ dài các cạnh của tam giác.
- p = (a + b + c) / 2 là nửa chu vi của tam giác.
Thay các giá trị vào, ta có:
p = (6 + 8 + 10) / 2 = 12 cm
S = √(12 * (12 - 6) * (12 - 8) * (12 - 10)) = √(12 * 6 * 4 * 2) = √288 = 24 cm²
Vậy diện tích của tam giác MNP là 24 cm².
Bài tập 2:
Tính diện tích tam giác có hai cạnh lần lượt là 8 cm và 10 cm và góc xen giữa hai cạnh là 45 độ.
Lời giải:
Dữ kiện đề bài:
- a = 8 cm
- b = 10 cm
- C = 45 độ
Áp dụng công thức, ta có:
Diện tích tam giác = 1/2 * 8 cm * 10 cm * sin(45°) = 40 cm² * 0.707 = 28.28 cm²
Vậy diện tích của tam giác là khoảng 28.28 cm².
Bài tập 3:
Tính diện tích tam giác vuông có cạnh góc vuông là 6 cm.
Trong bài toán này, ta được cho: cạnh góc vuông a = 6 cm
Vì đây là tam giác vuông, nên ta biết rằng: b = a = 6 cm
Suy ra: Diện tích tam giác = 1/2 * 6* 6= 18 cm²
Vậy diện tích của tam giác vuông có cạnh góc vuông là 6 cm là 18 cm².
Bài tập 4:
Một hình tam giác có đỉnh A, B và C. Biết rằng độ dài của đường cao từ đỉnh A là 6 cm và độ dài của cạnh AB là 8 cm. Tính diện tích hình tam giác đó.
Lời giải:
Để tính diện tích tam giác ABC, ta sử dụng công thức:
Diện tích tam giác = 1/2 * đáy * chiều cao
Trong đó:
- Đáy AB = 8 cm
- Chiều cao từ đỉnh A = 6 cm
Thay các giá trị vào công thức, ta có:
Diện tích tam giác = 1/2 * 8 cm * 6 cm = 24 cm²
Vậy S_ABC bằng 24 cm².
Bài tập nâng cao tự luyện tại nhà cho học sinh giỏi
Bài 1: Cho tam giác ABC có độ dài các cạnh là: AB = 12 cm, BC = 16 cm, AC = 20 cm. Tính diện tích.
Gợi ý: Sử dụng công thức Hê-rông để tính diện tích.
Bài 2: Một tam giác có ba đỉnh A, B, C. Biết rằng tọa độ của các đỉnh là: A(2, 3), B(6, 5), C(4, 9). Hãy cho biết diện tích của tam giác này.
Gợi ý: Sử dụng công thức tính diện tích tam giác khi biết tọa độ của ba đỉnh.
Bài 3: Cho một tam giác vuông ABC, trong đó góc vuông nằm tại đỉnh A. Biết rằng độ dài cạnh AB = 10 cm, độ dài cạnh AC = 24 cm. Xác định diện tích của hình tam giác.
Gợi ý: Sử dụng công thức diện tích tam giác vuông khi biết độ dài hai cạnh góc vuông.
Bài 4: Một tam giác có hai cạnh bằng nhau, mỗi cạnh dài 12 cm và góc xen giữa hai cạnh này bằng 60°. Tính diện tích của tam giác đó.
Gợi ý: Sử dụng công thức diện tích tam giác khi biết hai cạnh và góc xen giữa chúng.
Bài 5: Cho tam giác ABC có chu vi là 24 cm và bán kính đường tròn ngoại tiếp tam giác là 5 cm. Tính diện tích tam giác ABC.
Gợi ý: Sử dụng công thức diện tích tam giác khi biết chu vi và bán kính đường tròn nội tiếp.
Nắm vững cách tính diện tích hình tam giác bằng các công thức khác nhau không chỉ giúp các bạn giải quyết tốt các bài toán trong lĩnh vực toán học mà còn là nền tảng vững chắc để tiếp cận nhiều vấn đề thực tế. Hãy tiếp tục luyện tập và ứng dụng những kiến thức này, đảm bảo các bạn sẽ có thể giải quyết các bài toán phức tạp hơn trong tương lai.
