Z là tập hợp số gì? Z- là tập hợp số gì? Tất tần tật về tập Z

Z là tập hợp số gì ví dụ

Trong toán học có rất nhiều tập hợp số khác nhau biểu thị cho các loại số học tương ứng. Khi tìm hiểu các tập hợp số, nhiều người thắc mắc không biết Z là tập hợp số gì? Theo quy ước toán học, Z là tập hợp biểu thị các số nguyên. Tập hợp này bao gồm tất cả các số nguyên dương, số nguyên âm và số 0. Cụ thể, các phần tử của tập hợp Z có thể được liệt kê như sau: ..., -3, -2, -1, 0, 1, 2, 3, …

*Tìm hiểu Z là tập hợp số gì, Z- là tập hợp số gì giúp bạn giải quyết được các bài toán liên quan đến số nguyên Z*

Số nguyên là tất cả các số không bao gồm số thập phân hay phân số. Các số nguyên được sử dụng phổ biến trong các phép tính toán học và là nền tảng cho nhiều khái niệm trong đại số và lý thuyết số.

Tập hợp "Z" xuất phát từ tiếng Đức "Zahlen", có nghĩa là "số." Trong toán học, tập hợp các số nguyên Z đóng vai trò quan trọng trong nhiều lĩnh vực khác nhau, bao gồm số học, đại số và lý thuyết số. Hiểu rõ Z là tập hợp số gì và vận dụng tập hợp Z là nền tảng cho nhiều khái niệm và giúp bạn dễ dàng giải quyết các phép toán cơ bản.

Xem thêm:

Phát biểu định luật phản xạ ánh sáng chính xác và đầy đủ nhất

Các ví dụ về tập hợp Z trong toán học:

Ví dụ 1: Tập hợp các số nguyên từ -3 đến 3: { -3, -2, -1, 0, 1, 2, 3}
Ví dụ 2: Tập hợp các số nguyên lẻ: {..., -5, -3, -2, -1, 1, 3, 5, 7,...}
Ví dụ 3: Tập hợp các số nguyên chẵn: {..., -8, -6, -4, -2, 0, 2, 4, 6, 8,...}

2. Ký hiệu tập hợp Z trong toán học

Trong toán học, tập hợp Z được chia thành nhiều tập hợp con như Z+, Z- và số 0. Cụ thể như sau:

Tập hợp Z có số 0 không?

Tập hợp Z có bao gồm số 0. Tập hợp Z biểu thị tập hợp các số nguyên, bao gồm tất cả các số nguyên dương, số nguyên âm, và số 0. Cụ thể, tập hợp Z có thể được viết như sau:

Z = { …., -3, -2, -1, 0, 1, 2, 3,....}

Các số nguyên trong tập hợp Z được phân loại như sau:

Số nguyên dương: {1, 2, 3,...}
Số nguyên âm: {...., -3, -2, -1}
Số 0: {0}

Việc nắm rõ Z là tập hợp của số nào và những số nào thuộc tập hợp Z sẽ giúp bạn dễ dàng vận dụng để giải quyết các dạng toán có liên quan.

2.2. Z+ là tập hợp số gì?

Z+ là ký hiệu biểu thị tập hợp các số nguyên dương. Tập hợp này bao gồm tất cả các số nguyên lớn hơn 0. Cụ thể, tập hợp Z+ được viết như sau:

Z+ = { 1, 2, 3, 4, 5,...}

Điều này có nghĩa là Z+ chứa các số nguyên như 1, 2, 3, và cứ tiếp tục tăng dần mà không có giới hạn trên, nhưng không bao gồm số 0 và các số nguyên âm.

Z- là tập hợp số gì?

Để biết Z là tập hợp số gì, bạn cần nắm rõ Z là tập hợp số gì. Theo quy ước toán học, Z- là ký hiệu biểu thị tập hợp các số nguyên âm. Tập hợp này bao gồm tất cả các số nguyên nhỏ hơn 0. Cụ thể, tập hợp Z- được viết như sau:

Z- = {...., -7, -5, -4, -3, -2, -1}

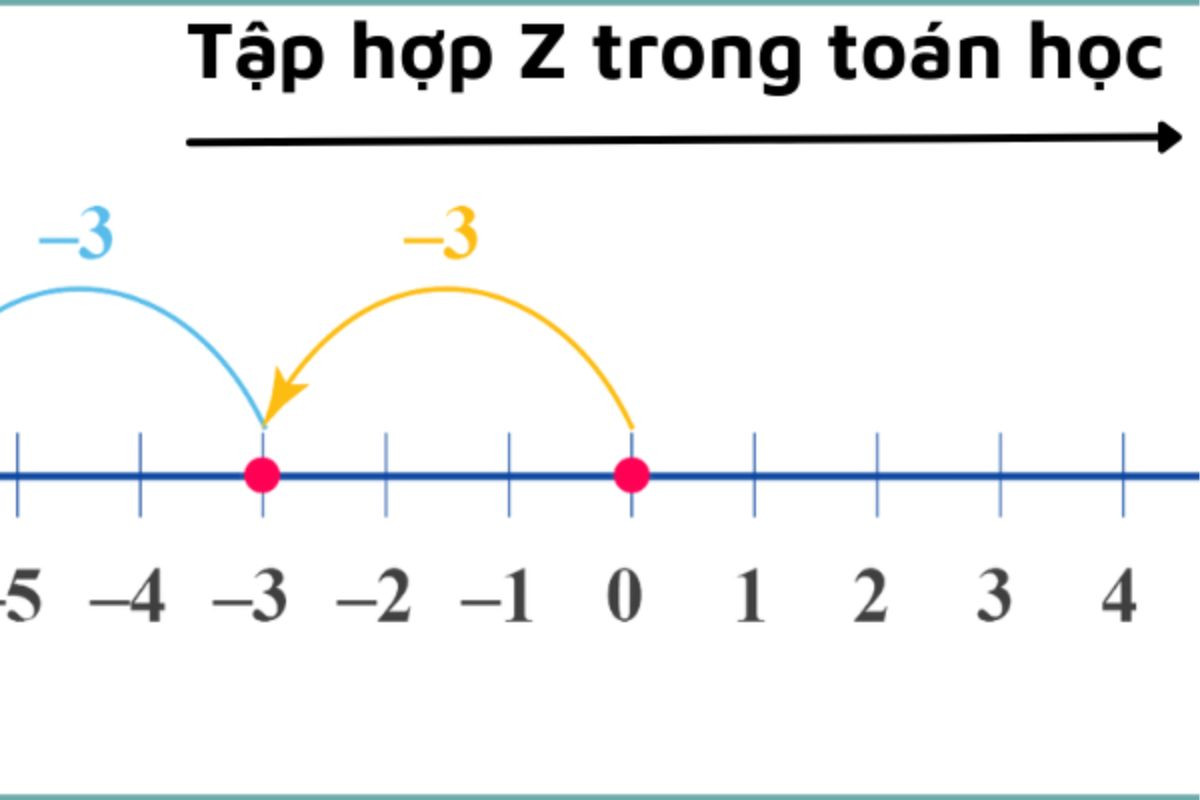
*Trong toán học, Z- là tập hợp các số nguyên âm bé hơn 0*

Điều này có nghĩa là Z- chứa các số nguyên như -1, -2, -3, và cứ tiếp tục giảm dần mà không có giới hạn dưới, nhưng không bao gồm số 0 và các số nguyên dương.

Tính chất của số nguyên Z

Z là tập hợp số nguyên nên mang nhiều tính chất đặc biệt. Hiểu Z là tập hợp số gì và nắm rõ các tính chất của tập hợp Z sẽ giúp bạn dễ dàng vận dụng tính toán các bài toán liên quan. Dưới đây là những tính chất của tập hợp số nguyên Z:

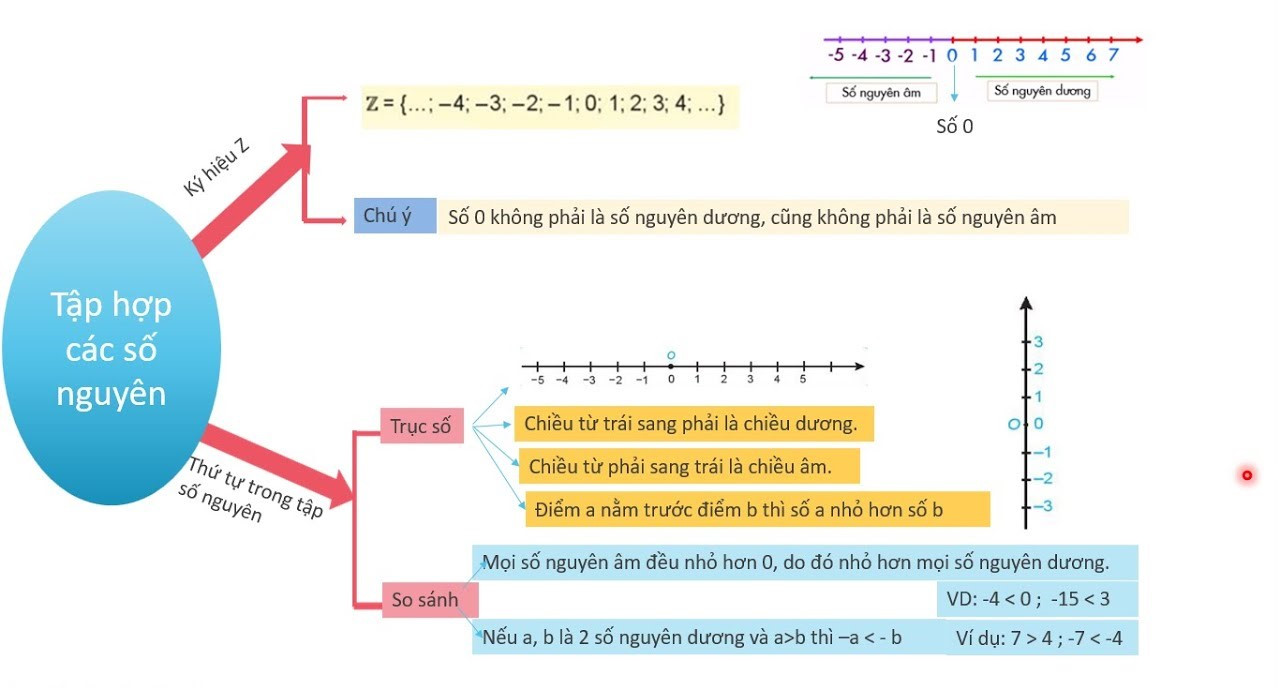
*Z gồm các số nguyên âm, số nguyên dương và số 0, tổng và hiệu của hai số nguyên cũng là một số nguyên*

Phép cộng và phép trừ: Tổng và hiệu của hai số nguyên bất kì luôn là một số nguyên. Ví dụ, nếu a và b đều là số nguyên thì a+ b và a - b cũng cho ra kết quả là số nguyên.
Phép nhân: Tích của hai số nguyên bất kì luôn là một số nguyên. Ví dụ, nếu a và b đều là số nguyên thì tích a * b cũng là số nguyên.
Phép chia: Thương của hai số nguyên chưa chắc đã là một số nguyên. Ví dụ 7 chia cho 2 bằng 3.5. Trong trường hợp này, 3.5 không phải là số nguyên.
Tính vô hạn: Tập hợp các số nguyên là vô hạn, tức là không thể liệt kê hết tất cả các số nguyên. Không có số nguyên dương lớn nhất và không có số nguyên âm nhỏ nhất.
Số nguyên dương nhỏ nhất: Số nguyên dương nhỏ nhất trong tập hợp Z là số 1.
Số nguyên âm lớn nhất: Số nguyên âm lớn nhất trong tập hợp Z là -1.
Tính chất của tập con hữu hạn: Trong một tập con hữu hạn của các số nguyên, luôn có số nguyên lớn nhất và số nguyên nhỏ nhất đã được xác định.

Quan hệ giữa tập hợp Z với các tập hợp số khác

Sau khi tìm hiểu tập hợp Z là những số nào, bạn sẽ biết được mối quan hệ giữa tập hợp Z với các tập hợp số khác. Cụ thể, tập hợp các số nguyên Z có mối quan hệ chặt chẽ với các tập hợp số khác trong toán học và bao gồm nhiều tập hợp con:

Quan hệ giữa tập hợp Z với tập hợp N

Trong toán học, N là tập hợp số tự nhiên, bao gồm các số nguyên dương. Vì tất cả các số tự nhiên đều là số nguyên dương nên N là tập hợp con của tập hợp Z, ký hiệu N ⊂ Z. Tập hợp số tự nhiên N được biểu diễn như sau:

N = {1, 2, 3, 4, 5,...}

Quan hệ giữa tập hợp Z với tập hợp Q

Khi tìm hiểu các tập hợp số trong toán học và biết được Z là tập hợp số gì, Q là tập hợp số gì, bạn sẽ xác định được mối quan hệ giữa hai tập số này. Trong toán học, Q là tập hợp các số hữu tỉ, bao gồm tất cả các số nguyên và các số được biểu diễn dưới dạng phân số với mẫu số khác 0.

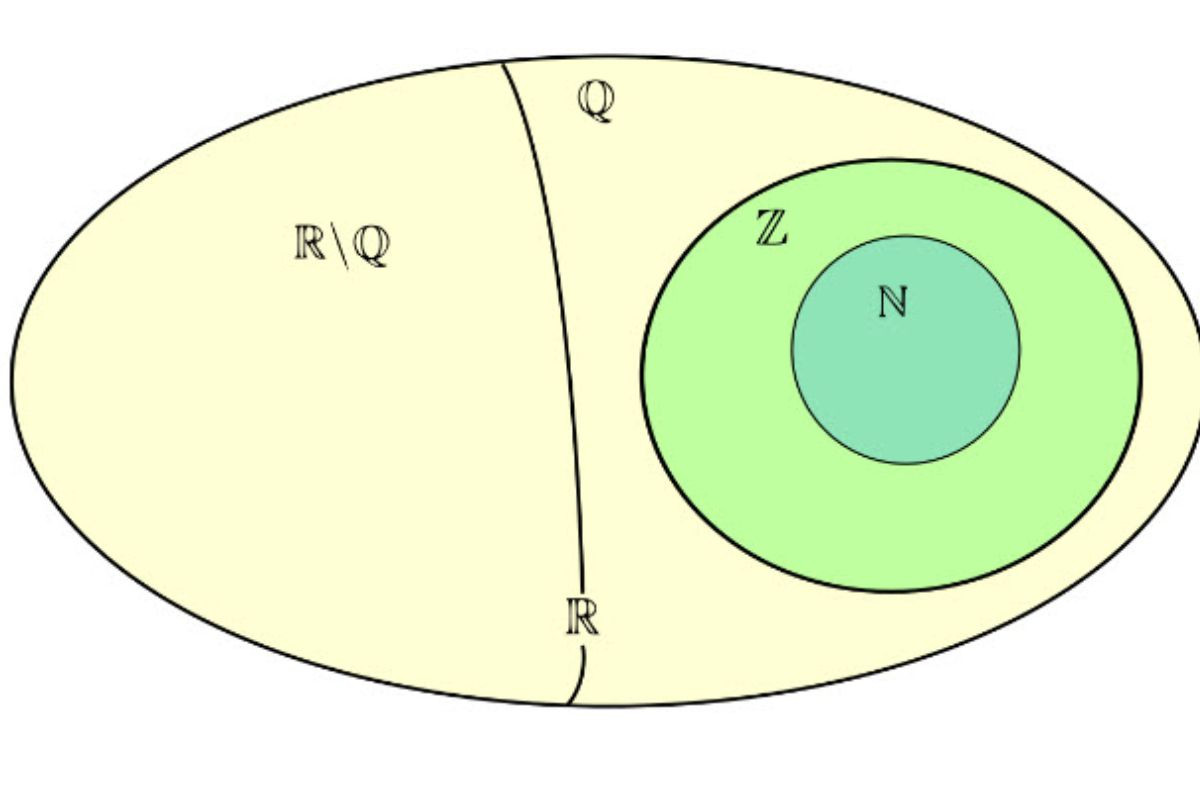
*Mối quan hệ giữa tập hợp số nguyên Z với các tập hợp số N, Q, R trong toán học*

Vì tất cả các số nguyên đều là số hữu tỉ nên Z là tập hợp con của tập hợp Q, ký hiệu là Z ⊂ Q. Tập hợp số hữu tỉ Q được biểu diễn như sau:

Q = { -⅚ , ½, 3,...}

Quan hệ giữa tập hợp Z với tập hợp R

Trong toán học, R là tập hợp các số thực, bao gồm tất cả các số hữu tỉ và vô tỉ. Bên cạnh đó, tập R còn bao gồm tất cả các số xuất hiện trên trục số. Do đó, Q là tập hợp con của tập R, đồng thời Z cũng là tập hợp con của tập R và ký hiệu là Z ⊂ R.

Tập hợp số thực R được biểu diễn như sau:

R = { -3, -2, 1, ⅓, 8, 3.14, 8,...}

Tóm lại:

Tập hợp số tự nhiên (N) là một tập hợp con của tập hợp số nguyên (Z).
Tập hợp số nguyên (Z) là một tập hợp con của tập hợp số hữu tỉ (Q).
Tập hợp số hữu tỉ (Q) là một tập hợp con của tập hợp số thực (R).
Tập hợp số thực (R) là một tập hợp con của tập hợp số phức (C).

Một số bài tập về tập hợp số nguyên Z

Để giải quyết các bài toán liên quan đến tập hợp Z, bạn cần hiểu rõ Z là tập hợp số gì, Z+ là tập hợp số gì, Z- là tập hợp số gì, đồng thời nắm rõ các tính chất cơ bản của tập hợp số nguyên Z. Dưới đây là một số dạng toán liên quan đến tập hợp Z mà bạn có thể tham khảo:

Dạng 1: Các phép toán với tập số nguyên Z:

Bạn có thể thực hiện các phép toán với các phần tử của tập hợp Z sau khi biết Z là tập hợp số gì. Các phép toán cơ bản bao gồm cộng, trừ, nhân và chia.

Ví dụ:

Tính giá trị: -8 + 3 * 2 = -2
Tính giá trị: 9 * (-2) - 11 = -29
Tính giá trị: (-50) : 2 + (-15) : 5 = -28

Dạng 2: Biểu diễn các điểm trên trục số:

Tập hợp Z bao gồm tất cả các số nguyên, bao gồm cả số nguyên dương, số nguyên âm và số 0. Còn trục số là một đường thẳng vô hạn mà trên đó mỗi điểm tương ứng với một số thực. Do đó, bạn hoàn toàn có thể biểu diễn các số thuộc tập hợp Z trên trục số. Chẳng hạn như sau:

*Biểu diễn các phần tử của tập hợp Z trên trục số*

Trong đó, mỗi số nguyên được biểu diễn bằng một điểm cụ thể trên trục số và chúng được cách đều nhau một khoảng cách bằng 1 đơn vị.

Dạng 3: Dạng toán tìm giá trị x:

Ngoài ra, bạn cũng có thể thực hiện các bài toán tìm x với các số nguyên trong tập hợp Z. Nói chung, các dạng toán liên quan đến tập số nguyên Z rất nhiều bởi nó là khái niệm quan trọng trong toán học.

Ví dụ: Tìm x biết 2x + 3 = 11

Cách giải:

Ta có: 2x + 3 = 11

=> 2 x = 11 - 3

=> 2x = 8

=> x = 8 : 2 = 4

Như vậy, x trong biểu thức trên có giá trị bằng 4.

Dạng 4: So sánh 2 số nguyên trong tập hợp Z:

Để so sánh các phần tử trong tập hợp Z, bạn cần biết Z là tập hợp số gì và nắm rõ các tính chất của nó. Theo đó, số nguyên dương luôn lớn hơn số nguyên âm và 0. Còn số nguyên âm luôn nhỏ hơn 0 và số nguyên dương. Khi so sánh các số cùng dấu, giá trị lớn hơn (hoặc giá trị tuyệt đối nhỏ hơn nếu là số âm) sẽ xác định số nào lớn hơn.

*Số nguyên dương lớn hơn 0 và lớn hơn số nguyên âm*

Một số ví dụ về dạng toán so sánh 2 số nguyên trong tập hợp Z như sau:

So sánh các số nguyên dương:

Số nguyên dương lớn hơn tất cả các số nguyên âm và 0.
Khi so sánh hai số nguyên dương, số nào có giá trị lớn hơn thì số đó lớn hơn.
Ví dụ: 5 > 3, 8 < 12

So sánh các số nguyên âm:

Số nguyên âm nhỏ hơn tất cả các số nguyên dương và 0.
Khi so sánh hai số nguyên âm, số nào có giá trị tuyệt đối lớn hơn thì số đó nhỏ hơn.
Ví dụ: -2 > -5, -7 < -3

So sánh với số 0:

Số 0 lớn hơn tất cả các số nguyên âm.
Số 0 nhỏ hơn tất cả các số nguyên dương.
Ví dụ: 0 < 3, 0> -8

Nắm rõ Z là tập hợp số gì và những tính chất của tập hợp Z trong toán học không chỉ giúp bạn hiểu rõ về cấu trúc và tính chất của các số nguyên mà còn là nền tảng để giải quyết các bài toán liên quan đến số nguyên. Đồng thời, biết Z- là tập hợp số gì, Z+ là tập hợp số gì giúp bạn tránh các sai sót nhỏ khi thực hiện phép tính và phép so sánh liên quan đến các phần tử trong tập hợp Z.