Tam giác cân là gì?
Trước khi khám phá công thức tính diện tích tam giác cân, hãy cùng ôn lại định nghĩa về tam giác đặc biệt này.
Tam giác cân là trường hợp khi tam giác có độ dài hai cạnh bất kỳ bằng nhau, từ đó kéo theo hai góc của tam giác bằng nhau. Tam giác đều là trường hợp đặc biệt của tam giác cân, trong đó ba cạnh và ba góc của tam giác đều bằng nhau.
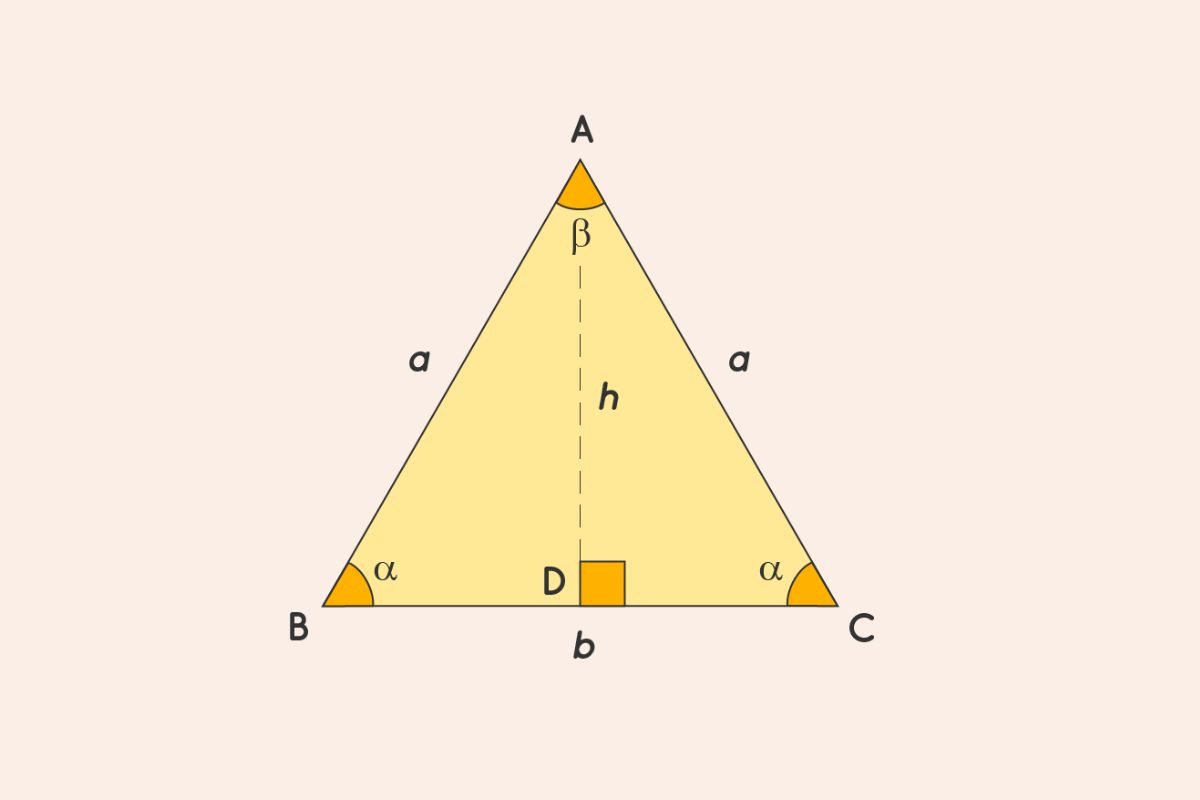
Một tam giác cân có hai cạnh dài bằng nhau và hai góc bằng nhau, các góc mà các cạnh này gặp cạnh thứ ba có hình dạng đối xứng. Nếu một đường vuông góc được vẽ từ giao điểm của hai cạnh bằng nhau với đáy của cạnh không bằng nhau thì tạo ra hai tam giác vuông.
Diện tích của một tam giác cân được biểu thị bằng đơn vị m², cm², dm².
Các công thức tính diện tích tam giác cân
Để chinh phục mọi bài toán diện tích tam giác cân, bạn cần thuộc lòng những công thức sau:
Sử dụng một cạnh và chiều cao
Diện tích tam giác cân đề cập đến tổng không gian được bao phủ bởi hình dạng 2-D. Diện tích của một tam giác cân có thể được tính theo nhiều cách dựa trên các phần tử đã biết của tam giác cân. Công thức cơ bản tổng quát có thể dùng để tính diện tích tam giác cân theo chiều cao là:
S = ½ × b × h
Trong đó b = đáy và h = chiều cao
Ví dụ: Cho tam giác cân ABC có AB = AC = 6cm, BC = 8cm. Diện tích tam giác ABC bằng:
Diện tích = 1/2 * 6cm * 8cm = 24cm²
Sử dụng cả ba cạnh
Nếu biết chiều dài các cạnh bằng nhau và đáy của một tam giác cân thì có thể tính được chiều cao của tam giác đó. Công thức tính diện tích tam giác cân khi sử dụng các cạnh được đưa ra là:
S = ½[√(a² − b² ⁄4) × b]
- a tương ứng là số đo các cạnh bằng nhau
- b = đáy của tam giác
Ví dụ: Cho một tam giác cân có hai cạnh bằng nhau có độ dài 6cm và cạnh đáy dài 8cm. Tính diện tích của tam giác cân đó.
Áp dụng công thức tính diện tích tam giác cân.
S= ½[√(6² − 8² ⁄4) × 8]
= ½[√(36 − 16) × 8]
= ½√20 × 8
= ½√160
= ½4√10
= 2√10
Độ dài hai cạnh và một góc xen giữa
S = ½ × a × b × sin(α)
- a là số đo các cạnh bằng nhau
- b là đáy của tam giác
Ví dụ: Cho tam giác cân ABC có AB = AC = 4cm, góc BAC = 45°. Diện tích tam giác ABC = 1/2 * 4cm * 4cm * sin(45°) = 4cm²
Cho hai góc và độ dài các cạnh giữa chúng
S = [a² ×sin(β)×sin(α)/ 2×sin(2π−α−β)]
- a = số đo các cạnh bằng nhau
- b = đáy của tam giác
- α = số đo các góc bằng nhau
- β = góc đối diện với đáy
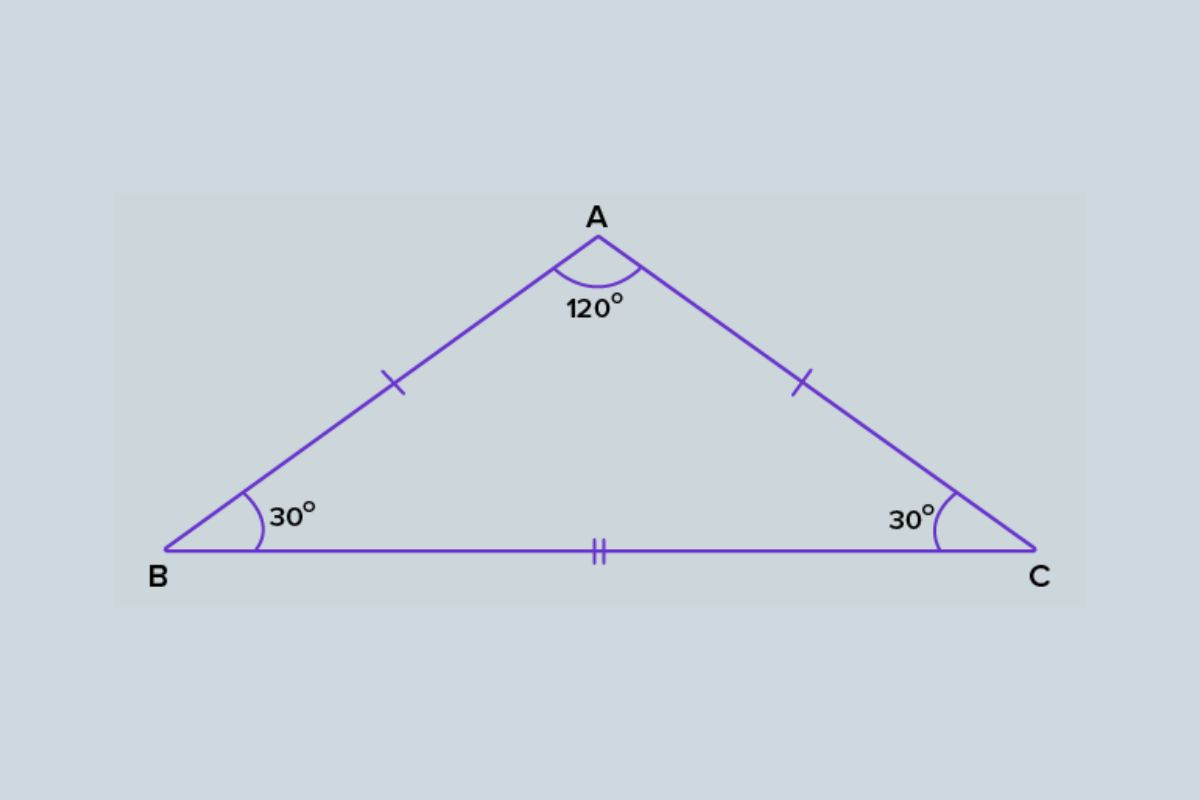
Ví dụ: Cho tam giác cân ABC có AB = AC = 5cm, góc BAC = 30°. Diện tích tam giác ABC = 5cm * 5cm / 4 * sin(2 * 30°) ≈ 3.85cm²
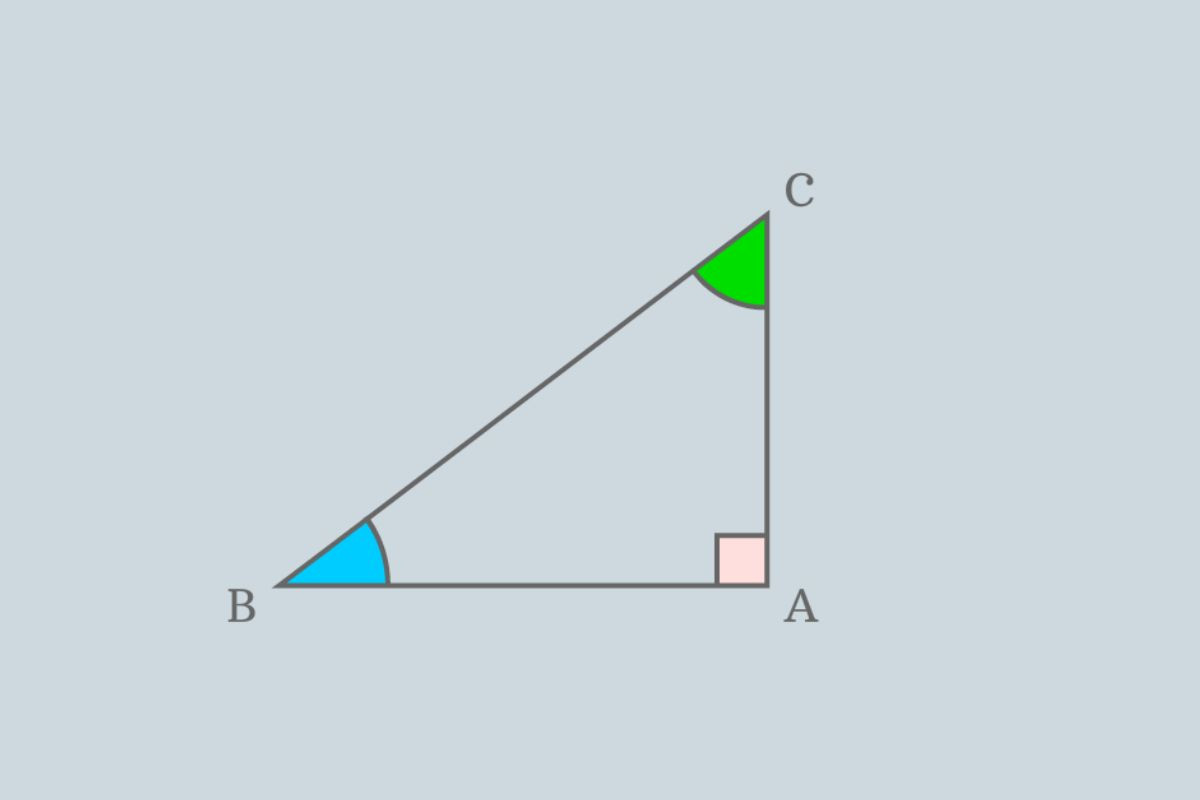
Công thức diện tích của tam giác vuông cân
Tam giác vuông cân là trường hợp đặc biệt hơn của một tam giác cân. Như vậy, diện tích tam giác cân ở đây được tính bằng công thức đơn giản: Diện tích = (cạnh góc vuông)² / 2
Ví dụ: Cho tam giác vuông cân ABC vuông tại A, có AB = AC = 3cm. Diện tích tam giác ABC = (3cm)² / 2 = 4.5cm² (theo máy tính casio online 580)
Tìm diện tích tam giác cân bằng công thức Heron
Diện tích tam giác cân còn có thể dễ dàng tính được bằng công thức Heron như được giải thích bên dưới đây. Công thức Heron được sử dụng để tính diện tích hình tam giác khi biết số đo 3 cạnh của nó.
Theo công thức Heron thì:
Diện tích = √[s(s−a)(s−b)(s−c)]
Trong đó, s = ½(a + b + c)
Xét trong một tam giác cân:
s = ½(a + a + b)
⇒ s = ½(2a + b)
Hoặc s = a + (b/2)
Như vậy, diện tích = √[s(s−a)(s−b)(s−c)] hoặc diện tích = √[s (s−a)² (s−b)]
⇒ Diện tích = (s−a) × √[s (s−b)]
Thay thế giá trị của “s”
⇒ Diện tích = (a + b/2 − a) × √[(a + b/2) × ((a + b/2) − b)]
⇒ Diện tích = b/2 × √[(a + b/2) × (a − b/2)]
Hoặc diện tích tam giác cân = b/2 × √(a² − b² /4)
Diện tích tam giác cân bằng phép đo lượng giác
Công thức tính diện tích tam giác cân sử dụng chiều dài 2 cạnh và góc xen giữa hoặc sử dụng 2 góc và chiều dài xen kẽ có thể được tính bằng cách sử dụng các khái niệm lượng giác cơ bản.
Sử dụng chiều dài 2 cạnh và góc giữa chúng
A = ½ × b × c × sin(α)
Sử dụng 2 góc và độ dài giữa chúng
A = [c² ×sin(β)×sin(α)/ 2×sin(2π−α−β)]
Bài tập ứng dụng
Bài 1: Cho tam giác cân ABC có AB = AC = 5cm, BC = 6cm. Hãy tính diện tích tam giác cân ABC đã cho.
Lời giải:
Áp dụng công thức tính diện tích tam giác cân bằng một cạnh và chiều cao:
Diện tích = 1/2 * BC * AH
Vì tam giác ABC cân, đường cao AH cũng là đường trung tuyến, chia BC thành hai đoạn BH = HC = 3cm.
Vậy diện tích = 1/2 * 6cm * 3cm = 9cm²
Bài 2: Một khu vườn hình tam giác cân có hai cạnh bên bằng nhau dài 8m, cạnh đáy dài 10m. Các bạn nhỏ muốn trồng hoa trên khu vườn này. Hãy tính diện tích mảnh đất cần trồng hoa.
Lời giải:
Áp dụng công thức tính diện tích tam giác cân bằng một cạnh và chiều cao:
Gọi chiều cao của tam giác cân là h.
Diện tích = 1/2 * 10m * h
Theo định lý Pitago trong tam giác vuông AHB:
h² = 8² - 5² = 39
Vậy h = √39 ≈ 6.24m
Diện tích = 1/2 * 10m * 6.24m ≈ 31.2m²
Bài 3: Một lá cờ đỏ tươi hình tam giác cân có cạnh đáy dài 20cm, chiều cao 15cm. Lá cờ được treo trên cột cờ cao 10m. Một cơn gió thổi qua khiến lá cờ nghiêng đi 30 độ so với phương ngang. Tính khoảng cách từ mép dưới của lá cờ đến mặt đất.
Lời giải:
Tính diện tích lá cờ
Diện tích = 1/2 * 20cm * 15cm = 150cm²
Tính khoảng cách từ mép dưới lá cờ đến đỉnh cột cờ
Khoảng cách = Chiều cao lá cờ + Chiều cao cột cờ = 15cm + 10m = 1015cm
Tính độ dài đoạn BC song song với mặt đất:
BC = AB * cos(30°) = 20cm * cos(30°) ≈ 17.32cm
Tính khoảng cách từ mép dưới lá cờ đến mặt đất
Khoảng cách = Chiều cao cột cờ + Độ dài đoạn BC * sin(30°) = 1015cm + 17.32cm * sin(30°) ≈ 1037.4cm
Bài 4: Một cánh đồng lúa hình tam giác cân có cạnh đáy dài 120m, hai cạnh bên bằng nhau dài 100m. Bà Hoa muốn chia cánh đồng thành các mảnh nhỏ bằng nhau để trồng các loại lúa khác nhau. Hỏi bà Hoa có bao nhiêu cách chia cánh đồng để mỗi mảnh có diện tích bằng nhau?
Lời giải:
Tính diện tích cánh đồng
Diện tích = 1/2 * 120m * √(100² - 60²) ≈ 5196m²
Tìm diện tích mỗi mảnh nhỏ
Giả sử mỗi mảnh nhỏ có diện tích x m².
Số lượng mảnh chia được: 5196m² / x m²
Tìm số cách chia cánh đồng
Vì cánh đồng có dạng hình tam giác cân nên số cách chia cần thỏa mãn hai điều kiện:
- Số lượng mảnh chia được phải là số nguyên.
- Các mảnh chia phải có hình dạng giống nhau (hình tam giác cân hoặc hình chữ nhật).
Với mỗi diện tích mảnh chia được x thỏa mãn hai điều kiện trên, sẽ có một cách chia cánh đồng hợp lệ.
Bài 5: Một ngôi nhà có mái hình tam giác cân với cạnh đáy dài 15m, chiều cao 8m. Trên mái nhà có lắp đặt hệ thống pin năng lượng mặt trời hình vuông có cạnh bằng 1m. Hệ thống pin được đặt cách đều nhau 1m theo cả hai cạnh đáy của mái nhà. Biết diện tích mái nhà được phủ kín bởi hệ thống pin. Hãy tính số lượng tấm pin năng lượng mặt trời cần thiết cho hệ thống.
Lời giải:
Tính diện tích mái nhà
Diện tích mái nhà = 1/2 * Cạnh đáy * Chiều cao = 1/2 * 15m * 8m = 60m²
Xác định diện tích một tấm pin
Diện tích một tấm pin = Cạnh pin * Cạnh pin = 1m * 1m = 1m²
Tính số lượng tấm pin cần thiết
Số lượng tấm pin = Diện tích mái nhà / Diện tích một tấm pin = 60m² / 1m² = 60 tấm
Vậy cần 60 tấm pin năng lượng mặt trời để phủ kín mái nhà.
Bài 6: Tìm diện tích, đường cao và chu vi của một tam giác cân khi biết a = 12 cm, b = 7 cm.
Lời giải:
Chu vi của một tam giác cân
= 2a + b
= 2(12) + 7 cm
= 24 + 7 cm
P = 31cm
Độ cao của một tam giác cân
= √(a² − b 2 ⁄4)
= √(12² −7²/4) cm
= √(144−49/4) cm
= √(144−12,25) cm
= √131,75 cm
h = 11,478 cm
Diện tích của một tam giác cân
= (b×h)/2
= (7×11,478)/2cm²
= 80,346/2cm²
= 40,173 cm²

Bài 7: Tìm độ dài đáy của một tam giác cân có diện tích là 243 cm² , đường cao của tam giác đó là 9 cm.
Lời giải:
Diện tích tam giác, A = 243 cm²
Chiều cao của tam giác (h) = 9 cm
Đáy tam giác = b =?
Diện tích Tam giác cân = (1/2) × b × h
243 = (1/2) × b × 9
243 = (b × 9)/2
b = (243 × 2)/9
b = 54cm
Vậy đường cao của tam giác cân đã cho là 54cm.
Bài 8: Một mảnh vườn hình tam giác cân có hai cạnh bên bằng nhau dài 50m, cạnh đáy dài 70m. Người ta trồng hoa trên 60% diện tích mảnh vườn. Tính diện tích đất trồng hoa.
Lời giải:
Tính diện tích mảnh vườn
Áp dụng công thức tính diện tích tam giác cân bằng một cạnh và chiều cao:
Diện tích = 1/2 * Cạnh đáy * Chiều cao
Vì tam giác cân, đường cao hạ từ đỉnh xuống cạnh đáy cũng là đường trung tuyến, chia cạnh đáy thành hai đoạn bằng nhau.
Gọi chiều cao mảnh vườn là h.
Diện tích = 1/2 * 70m * h
Tính chiều cao mảnh vườn
Theo định lý Pitago ta được:
h² = 50² - (70/2)² = 625
Vậy h = √625 ≈ 25m
Tính diện tích đất trồng hoa
Diện tích đất trồng hoa = 60% * Diện tích mảnh vườn
Diện tích mảnh vườn = 1/2 * 70m * 25m = 875m²
Diện tích đất trồng hoa = 60/100 * 875m² = 525m²
Vậy diện tích đất trồng hoa là 525m².
Bài viết này đã cung cấp cho bạn các công thức và ví dụ minh họa chi tiết về cách tính diện tích tam giác cân, cùng với các bài tập ứng dụng từ cơ bản đến nâng cao. Hy vọng những kiến thức này sẽ giúp bạn giải quyết thành công mọi bài toán về diện tích tam giác cân mà bạn gặp phải.
