Hợp số là gì?
Trong toán học, chắc hẳn bạn đã từng nghe đến hợp số. Nếu chưa học qua thì không ai có thể hiểu rõ hợp số là gì và cách vận dụng ra sao. Cho những ai chưa biết hợp số là gì thì đây là một số nguyên lớn hơn 1 và có nhiều hơn hai ước số. Nói cách khác, hợp số là số có thể chia hết cho các số nguyên khác ngoài 1 và chính nó. Điều này có nghĩa là ngoài 1 và chính nó, hợp số có ít nhất một ước số khác.

Ví dụ:
- Số 4 là hợp số vì ngoài 1 và 4, nó còn chia hết cho 2 (ước số của 4 là 1, 2 và 4).
- Số 6 là hợp số vì nó chia hết cho 1, 2, 3 và 6 (ước số của 6 là 1, 2, 3 và 6).
Ngược lại với hợp số là số nguyên tố. Số nguyên tố là những số chỉ có đúng hai ước số là 1 và chính nó. Ví dụ, số 5 là số nguyên tố vì nó chỉ có hai ước số là 1 và 5.
Hợp số là những số nào?
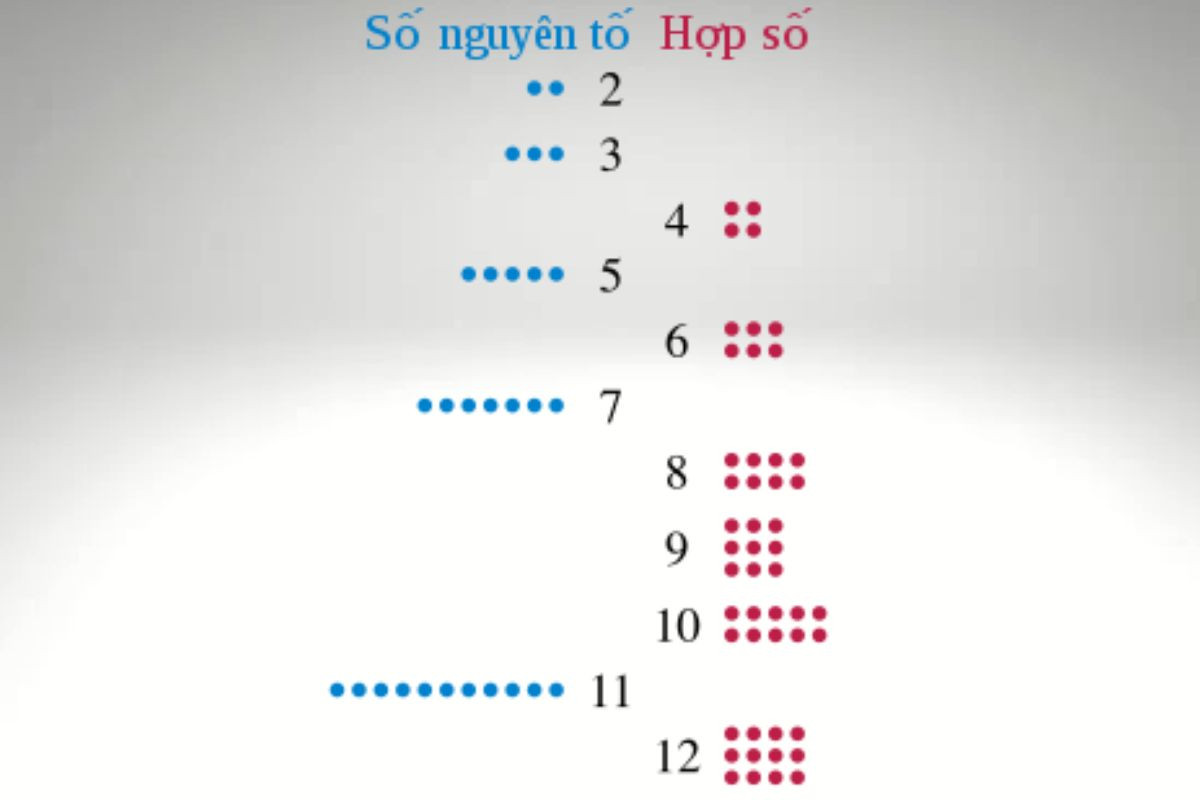
Sau khi hiểu rõ hợp số là gì, bạn sẽ dễ dàng xác định những số nào là hợp số. Hợp số là những số nguyên lớn hơn 1 và có nhiều hơn hai ước số. Dưới đây là danh sách các hợp số nhỏ hơn 20 mà bạn có thể tham khảo:
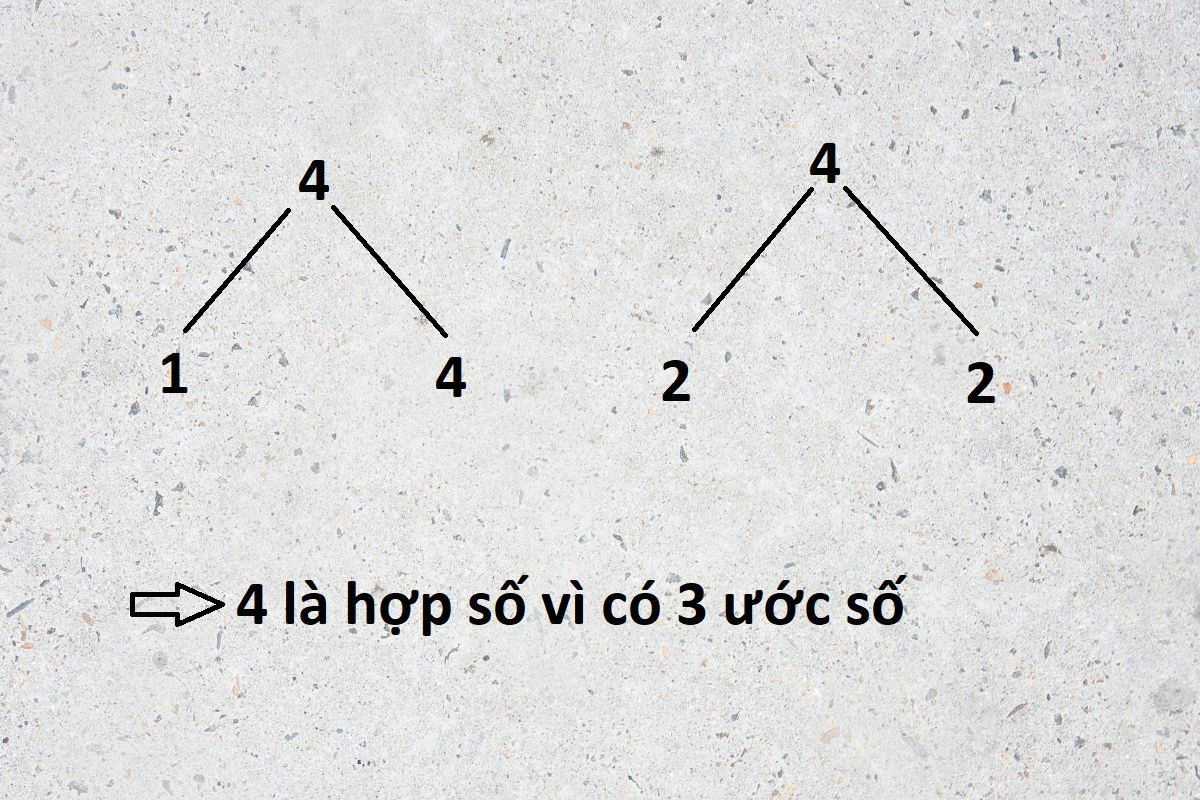
- 4 là hợp số (ước số: 1, 2, 4)
- 6 là hợp số (ước số: 1, 2, 3, 6)
- 8 là hợp số (ước số: 1, 2, 4, 8)
- 9 là hợp số (ước số: 1, 3, 9)
- 10 là hợp số (ước số: 1, 2, 5, 10)
- 12 là hợp số (ước số: 1, 2, 3, 4, 6, 12)
- 14 là hợp số (ước số: 1, 2, 7, 14)
- 15 là hợp số (ước số: 1, 3, 5, 15)
- 16 là hợp số (ước số: 1, 2, 4, 8, 16)
- 18 là hợp số (ước số: 1, 2, 3, 6, 9, 18)
- 20 là hợp số (ước số: 1, 2, 4, 5, 10, 20)
Danh sách các hợp số tiếp tục vô hạn, bao gồm mọi số nguyên lớn hơn 1 không phải là số nguyên tố. Các số nguyên tố (là số chỉ có hai ước số là 1 và chính nó) không phải là hợp số. Ví dụ, 2, 3, 5, 7, 11, 13, 17, 19 là các số nguyên tố nhỏ hơn 20.
Đặc điểm của hợp số
Hợp số là số nguyên lớn hơn 1 và có nhiều hơn hai ước số. Dưới đây là các đặc điểm chính của hợp số mà bạn có thể tham khảo:

- Nhiều hơn hai ước số: Hợp số có ít nhất ba ước số, bao gồm 1, chính nó và ít nhất một ước số khác. Ví dụ, số 4 có các ước số là 1, 2 và 4.
- Chia hết cho các số khác ngoài 1 và chính nó: Hợp số có thể chia hết cho các số khác ngoài 1 và chính nó. Ví dụ, số 6 chia hết cho 1, 2, 3 và 6 nên số 6 là hợp số.
- Không phải là số nguyên tố: Ngược lại với hợp số, số nguyên tố chỉ có hai ước số là 1 và chính nó. Do đó, bất kỳ số nguyên nào không phải là số nguyên tố (và lớn hơn 1) đều là hợp số.
- Tính chất phân tích thành thừa số nguyên tố: Hợp số có thể được phân tích thành tích của các số nguyên tố. Ví dụ, 12 là hợp số vì nó có thể được phân tích thành 2 × 2 × 3.
- Bất kỳ số chẵn nào lớn hơn 2 đều là hợp số: Tất cả các số chẵn lớn hơn 2 đều có ít nhất ba ước số (1, 2 và chính nó), vì vậy chúng đều là hợp số. Ví dụ, số 8 (có các ước số 1, 2, 4 và 8).
- Một số lẻ cũng có thể là hợp số: Không chỉ số chẵn, một số lẻ cũng có thể là hợp số nếu nó có nhiều hơn hai ước số. Ví dụ, số 9 (có các ước số 1, 3 và 9).
- Có vô số các hợp số: Sau khi biết hợp số là gì, bạn sẽ thấy có rất nhiều hợp số, miễn là các số có nhiều hơn hai ước số
Dựa vào các đặc điểm trên, bạn có thể xác định được hợp số giữa hàng triệu các số tự nhiên khác nhau, đồng thời phân biệt được nó với các số nguyên tố trong toán học.
4. Cách phân tích một số ra thừa số nguyên tố dễ nhất
Để phân tích một số ra thừa số nguyên tố, đầu tiên bạn cần phải hiểu rõ hợp số là gì và áp dụng phương pháp phân tích phù hợp. Dưới đây là các cách phân tích một số ra thừa số nguyên tố đơn giản nhất mà bạn có thể tham khảo và áp dụng:
Phân tích theo phương pháp cột dọc
Áp dụng phương pháp cột dọc là cách đơn giản nhất để phân tích một số ra thừa số nguyên tố. Cách thực hiện như sau:
- Bước 1: Đầu tiên, bạn cần chia số nguyên cần phân tích cho ước số nguyên tố nhỏ nhất của số đó.
- Bước 2: Lấy thương vừa tìm được chia cho cùng ước số nguyên tố. Thực hiện liên tục cho đến khi thương bằng 1.
- Bước 3: Ở mỗi bước, bạn cần ghi chú lại các số chia.

Ví dụ về phân tích một số ra thừa số nguyên tố theo phương pháp cột dọc:
Ví dụ 1: Phân tích số 60
60 | 2
30 | 2
15 | 3
5 | 5
1
Như vậy ta được kết quả: 60 = 2 x 2 x 3 x 5 hay 60 = 2^2 x 3 x 5
Ví dụ 2: Phân tích số 100
100 | 2
50 | 2
25 | 5
5 | 5
1
Như vậy ta được kết quả: 100 = 2 x 2 x 5 x 5 = 2^2 x 5^2
Phân tích theo phương pháp rẽ nhánh
Ngoài ra bạn cũng có thể phân tích một số ra thừa số nguyên tố dựa trên phương pháp rẽ nhánh. Cách thực hiện như sau:
- Bước 1: Đầu tiên, bạn cần tìm ra ước số nguyên nhỏ nhất của số mà mình muốn phân tích.
- Bước 2: Viết số cần phân tích thành tích của ước số nguyên mà mình vừa tìm được với một số số nguyên khác.
- Bước 3: Tiếp theo, tìm tiếp ước số nguyên của số vừa tìm được tại bước 2, sau đó tiếp tục lặp lại quá trình trên cho đến khi tất cả các thừa số đều là số nguyên tố.
- Bước 4: Kết quả cuối cùng là tích của các thừa số nguyên tố.
Ví dụ về cách phân tích một số ra thừa số nguyên tố theo phương pháp rẽ nhánh:
Ví dụ: Phân tích số 60
- 60 chia hết cho 2 nên 2 là ước số nguyên nhỏ nhất của 60, như vậy ta có 60 = 2 x 30
- 30 chia hết cho 2 nên 2 là ước số nguyên nhỏ nhất của 30, như vậy ta có 30 = 2 x 15
- 15 chia hết cho 3 và không chia hết cho 2 nên 3 là ước số nguyên nhỏ nhất của 15, như vậy ta có 15 = 3 x 5
- 5 chia hết cho 5 nên 5 là ước số nguyên của 5, như vậy ta có 5 = 5 x 1
=> Kết quả như sau: 60 = 2 x 2 x 3 x 5 = 2^2 x 3 x 5
Các ứng dụng của hợp số cụ thể nhất
Hiểu rõ hợp số là gì giúp bạn dễ dàng ứng dụng hợp số vào các dạng toán khác nhau, cụ thể như sau:
Phân tích số
Trong toán học, bạn có thể ứng dụng tính chất của hợp số để phân tích các số ra thừa số nguyên tố. Tuy nhiên, để làm được điều này thì bắt buộc bạn phải hiểu hợp số là gì cũng như nắm rõ các đặc điểm của hợp số.
Khi phân tích một số ra thừa số nguyên tố, bạn có thể sử dụng phương pháp cột dọc hoặc rẽ nhánh như đã hướng dẫn ở trên. Thông qua đó, bạn có thể tìm ra tất cả các thừa số nguyên tố của một số một cách dễ dàng và có hệ thống.
Việc phân tích số thành thừa số nguyên tố có nhiều ứng dụng trong toán học và các lĩnh vực khác như mã hóa, mật mã học và các thuật toán phức tạp. Đặc biệt, trong lĩnh vực mật mã học, việc phân tích số thành các thừa số nguyên tố là cực kỳ quan trọng trong quá trình mã hóa và giải mã thông tin.
Giải mã
Hợp số có thể ứng dụng trong quá trình giải mã thông tin được mã hóa bằng các thuật toán mã hóa đối xứng. Một trong những ứng dụng phổ biến của hợp số trong giải mã là trong việc phân tích và tìm ra các thừa số nguyên tố của một số nguyên lớn, đặc biệt trong các hệ thống mật mã dựa trên RSA.
Thuật toán RSA (Rivest-Shamir-Adleman) là một trong những thuật toán mã hóa đối xứng phổ biến nhất được sử dụng trong bảo mật thông tin. Trong thuật toán RSA, để tạo ra khóa công khai và khóa riêng tư, bạn cần chọn hai số nguyên tố lớn và tính tích của chúng, gọi là số nguyên tố công khai và số nguyên tố riêng tư.
Khi một thông điệp được mã hóa bằng RSA, thông điệp đó thường được biểu diễn dưới dạng một số nguyên n lớn. Để giải mã thông điệp, bạn cần phải hiểu hợp số là gì và tìm ra các thừa số nguyên tố của n. Quá trình này cần sử dụng các thuật toán phân tích số thành thừa số nguyên tố, và hợp số đóng vai trò quan trọng.
Lý thuyết số
Hợp số là kết quả của việc phân tích số nguyên thành tích của các số nguyên tố. Phân tích số ra các thừa số nguyên tố là một phần quan trọng của lý thuyết số và đóng vai trò quan trọng trong nhiều ứng dụng khác nhau, từ mật mã học đến lập trình.
Bên cạnh đó, trong quá trình sàng nguyên tố, chúng ta tìm kiếm tất cả các số nguyên tố nhỏ hơn một giá trị đã cho. Để thực hiện điều này, ta cần phải biết hợp số là gì, những số nào là hợp số để loại bỏ chúng khỏi danh sách.
Ngoài ra, trong nghiên cứu về lý thuyết số, các bài toán liên quan đến các tính chất của hợp số đặc biệt phức tạp và được nghiên cứu sâu rộng. Ví dụ như bài toán phân tích số nguyên tố lớn ra thừa số nguyên tố, bài toán RSA và các bài toán về phân phối các số nguyên tố.
Chia hết
Trong việc giải các bài toán về số học cơ bản, ta thường cần xác định tính chia hết giữa các số. Sử dụng kiến thức về hợp số, ta có thể dễ dàng xác định xem một số có chia hết cho một số khác không và từ đó giải quyết các bài toán liên quan đến phép chia một cách nhanh chóng.
Một số dạng toán về hợp số thường gặp
Nếu đã hiểu rõ hợp số là gì, bạn có thể ứng dụng tính chất của hợp số để giải quyết các dạng toán chia hết, tìm ước số nguyên,... Dưới đây là một số dạng toán về hợp số thường gặp:

Dạng 1: Phân tích số 150 ra thừa số nguyên tố:
=> Áp dụng phương pháp phân tích cột dọc:
150 | 2
75 | 3
25 | 5
5 | 5
1
=> Kết quả 150 = 2 x 3 x 5 x 5
Dạng 2: Tìm số nguyên nhỏ nhất chia hết cho 10
- Danh sách các số nguyên tố bé hơn hoặc bằng 10: 2, 3, 5, 7
- 10 chia hết cho 2
=> Số nguyên tố nhỏ nhất chia hết cho 10 là 2
Dạng 3: Tìm số ước số của hợp số 20:
- Số ước số của hợp số có dạng: n = (a + 1) * (b + 1) * (c + 1)
- Trong đó: a, b và c là các số mũ trong việc phân tích thừa số nguyên tố của hợp số đó.
- Ta có: 20 = 2 x 2 x 5 = 2^2 x 5 => a = 2, b = 1, c = 0
=> Như vậy, số ước số của hợp số 20 bằng (2 + 1) * (1 + 1) * (1 + 0) = 6
Một số thắc mắc khác
Ngoài hợp số là gì, còn có rất nhiều thắc mắc liên quan đến hợp số như:
1 có phải là hợp số không?
1 không phải là hợp số vì một số được coi là hợp số nếu nó lớn hơn 1 và có nhiều hơn 2 ước số. Bên cạnh đó, số 1 cũng không phải là một số nguyên tố.
2 có phải là hợp số không?
Số 2 không phải là hợp số vì một số được coi là hợp số nếu nó lớn hơn 1 và có nhiều hơn 2 ước số. Số 2 chỉ có hai ước số là 1 và chính nó, nên không thỏa mãn định nghĩa của hợp số.
Hiểu rõ hợp số là gì và các đặc điểm của hợp số giúp bạn phân biệt và áp dụng chúng trong phân tích số, xác định tính chia hết và hiểu sâu hơn về cấu trúc số học. Kiến thức này cũng có thể được áp dụng rộng rãi trong các lĩnh vực khác như công nghệ và kinh tế.
