Đường trung tuyến là gì?
Trong hình học, bạn sẽ thường xuyên gặp các dạng bài tập liên quan đến đường trung tuyến. Nếu không biết đường trung tuyến là gì và tính chất của nó như thế nào, bạn sẽ không thể giải được những bài toán liên quan.

Cho những ai đang thắc mắc đường trung tuyến là gì, đây là đoạn thẳng nối từ một đỉnh của tam giác đến trung điểm của cạnh đối diện. Khi vẽ đường trung tuyến, đoạn thẳng này chia cạnh đối diện thành hai phần bằng nhau. Nói một cách dễ hiểu, đường trung tuyến là đường thẳng đi qua trung điểm của cạnh đối diện.
Trong toán hình, đường trung tuyến không chỉ là một khái niệm quan trọng mà nó còn ứng dụng vào nhiều dạng bài toán khác nhau, từ đơn giản đến phức tạp. Do đó, việc hiểu rõ đường trung tuyến là gì sẽ giúp bạn biết cách vận dụng các tính chất của nó để giải quyết các bài toán liên quan.
Tính chất đường trung tuyến
Dựa vào tính chất đường trung tuyến trong tam giác, bạn có thể tính được độ dài đường trung tuyến hay cạnh đối diện và biết được đường trung tuyến là đường như thế nào. Tuy nhiên, tính chất đường trung tuyến trong tam giác thường sẽ khác với tính chất đường trung tuyến trong tam giác đều, tam giác cân và tam giác vuông. Cụ thể như sau:
Tính chất đường trung tuyến trong một tam giác bất kỳ
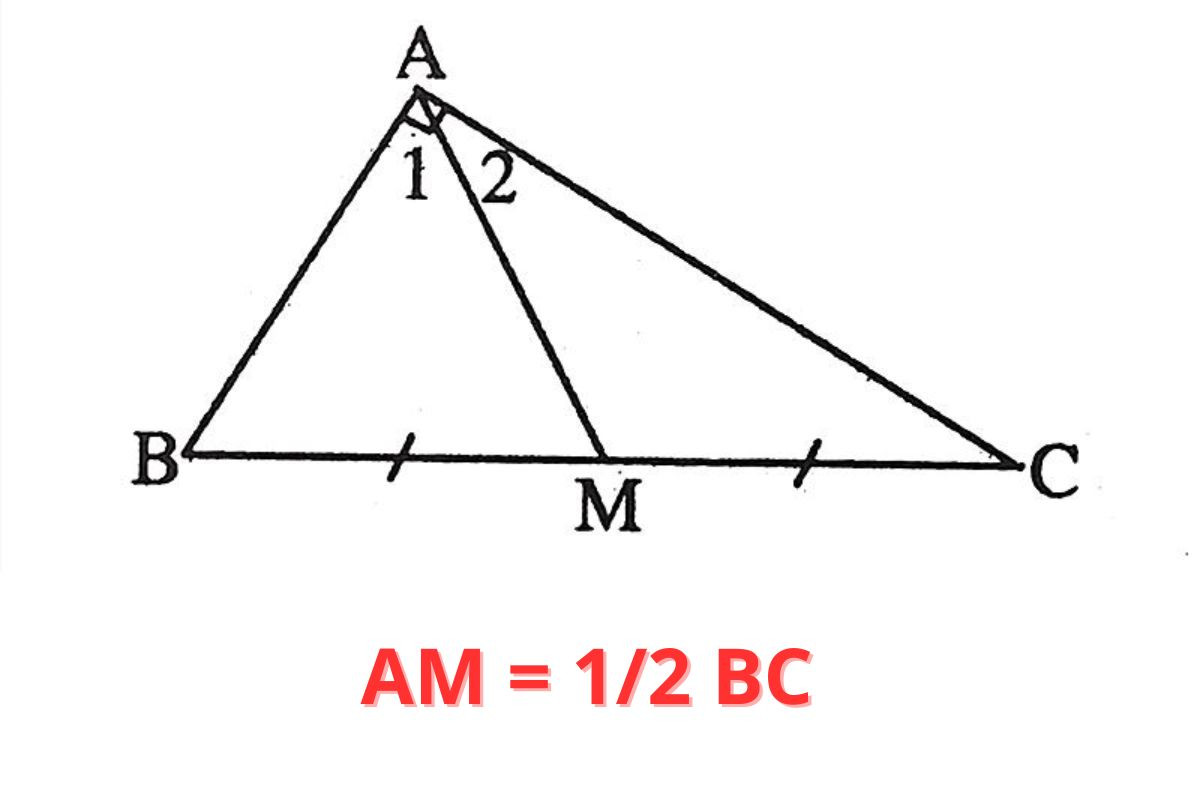
Trong một hình tam giác bất kỳ, đường trung tuyến chính là đoạn thẳng nối từ một đỉnh của tam giác đến trung điểm của cạnh đối diện. Trong tam giác thường, đường trung tuyến ứng với cạnh huyền có độ dài bằng ½ độ dài cạnh huyền.
Ví dụ: Tam giác ABC có cạnh huyền BC và đường trung tuyến AM. Như vậy, AM có độ dài bằng ½ độ dài đoạn BC.
Tính chất của đường trung tuyến trong một tam giác vuông
Trong một tam giác vuông, đường trung tuyến thực chất là đoạn thẳng nối từ một đỉnh vuông góc của tam giác đến trung điểm của cạnh huyền. Tam giác vuông có một góc 90 độ, do đó, đường trung tuyến chia diện tích tam giác thành hai phần bằng nhau.
Tính chất đường trung tuyến trong tam giác vuông: Trong tam giác vuông, đường trung tuyến ứng với cạnh huyền có độ dài bằng nửa cạnh huyền. Ví dụ, cạnh huyền có độ dài là a thì độ dài đường trung tuyến là a/2.
Tính chất đường trung tuyến trong một tam giác cân
Tam giác cân là dạng tam giác có hai cạnh bằng nhau. Vậy trong tam giác cân, đường trung tuyến là gì? Đường trung tuyến trong một tam giác cân chính là đoạn thẳng nối từ đỉnh của tam giác đến trung điểm của cạnh đối diện. Tam giác cân cũng có 3 đường trung tuyến xuất phát từ 3 đỉnh của tam giác.
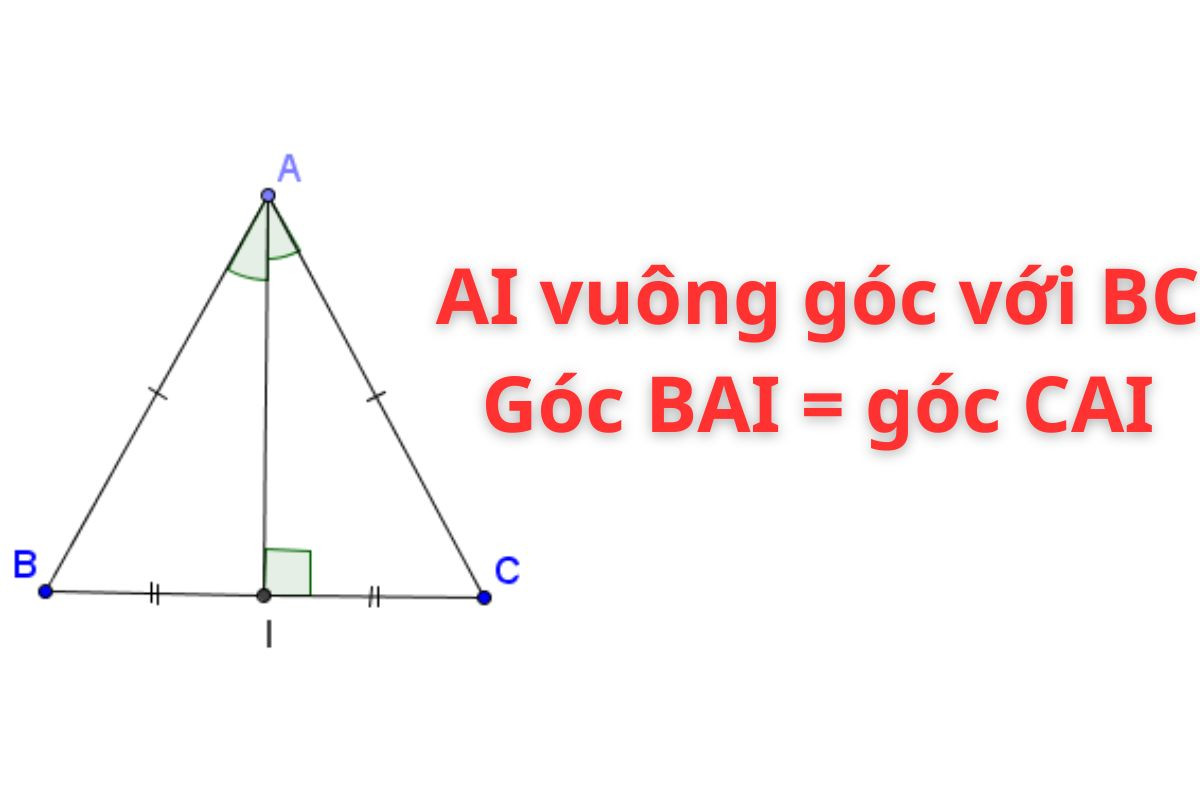
Tính chất đường trung tuyến trong tam giác cân có sự khác biệt so với tam giác vuông và tam giác thường, cụ thể như sau:
- Đường trung tuyến trong tam giác cân chia tam giác đó thành hai tam giác nhỏ có diện tích bằng nhau.
- Đường trung tuyến xuất phát từ đỉnh cân vuông góc với cạnh huyền. Ví dụ, tam giác ABC cân tại A và có đường trung tuyến là AM. Như vậy, đoạn thẳng AM vuông góc với BC.
- Hai đường trung tuyến xuất phát từ hai đỉnh còn lại của tam giác cân có độ dài bằng nhau. Ví dụ, tam giác ABC cân tại A và có đường trung tuyến là AM, BE, CF. Như vậy đường trung tuyến BE và CF có độ dài bằng nhau.
Tính chất đường trung tuyến trong một tam giác đều
Tam giác đều là dạng tam giác có ba cạnh có độ dài bằng nhau. Đường trung tuyến trong tam giác đều là đoạn thẳng nối từ đỉnh của tam giác đến trung điểm của cạnh đối diện. Tam giác đều cũng có 3 đường trung tuyến xuất phát từ 3 đỉnh của tam giác.
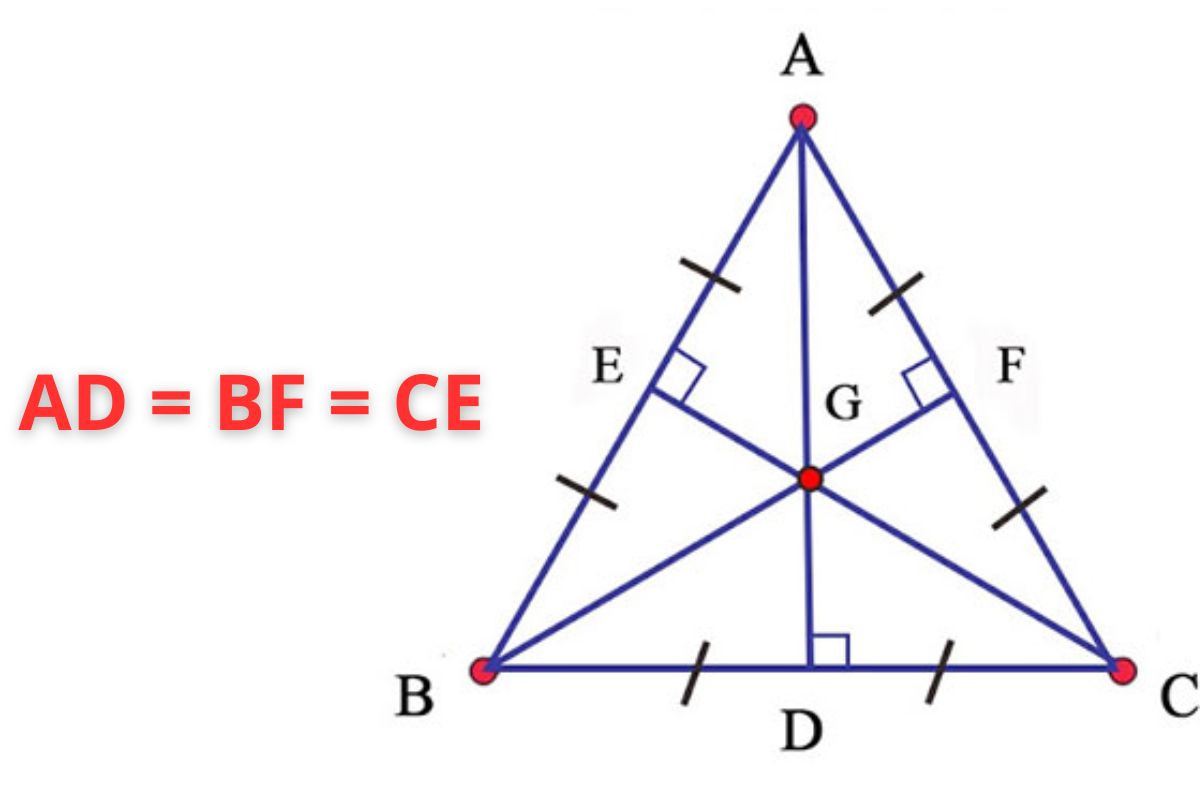
Ngoài việc tìm hiểu đường trung tuyến là gì, bạn cũng cần nắm rõ tính chất đường trung tuyến trong tam giác đều để ứng dụng vào việc giải các dạng bài tập toán liên quan. Tính chất đường trung tuyến trong một tam giác đều được quy định như sau:
- 3 đường trung tuyến xuất phát từ 3 đỉnh trong tam giác đều có độ dài bằng nhau.
- 3 đường trung tuyến xuất phát từ 3 đỉnh trong tam giác đều cắt nhau tại trọng tâm của tam giác.
- 3 đường trung tuyến xuất phát từ 3 đỉnh trong tam giác đều chia tam giác đó thành 6 tam giác nhỏ có diện tích bằng nhau.
- Đường trung tuyến trong tam giác đều có độ dài như sau:
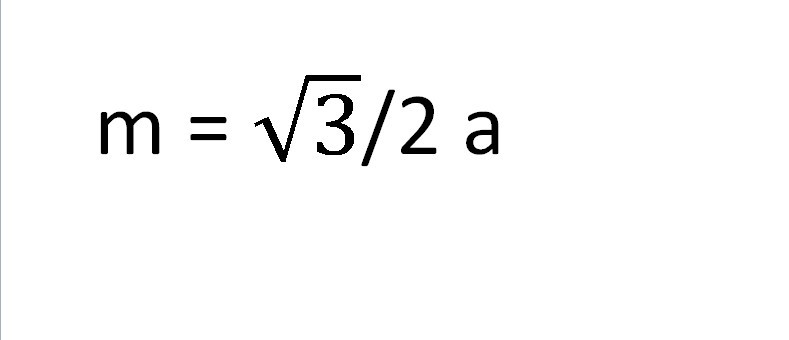
Giao của 3 đường trung tuyến là gì?
Giao điểm của ba đường trung tuyến trong một tam giác gọi là trọng tâm của tam giác đó. Từ trọng tâm của tam giác, bạn có thể vẽ được 3 đoạn thẳng nối với 3 trung điểm của tam giác đó và tạo ra đường 3 đường trung tuyến.
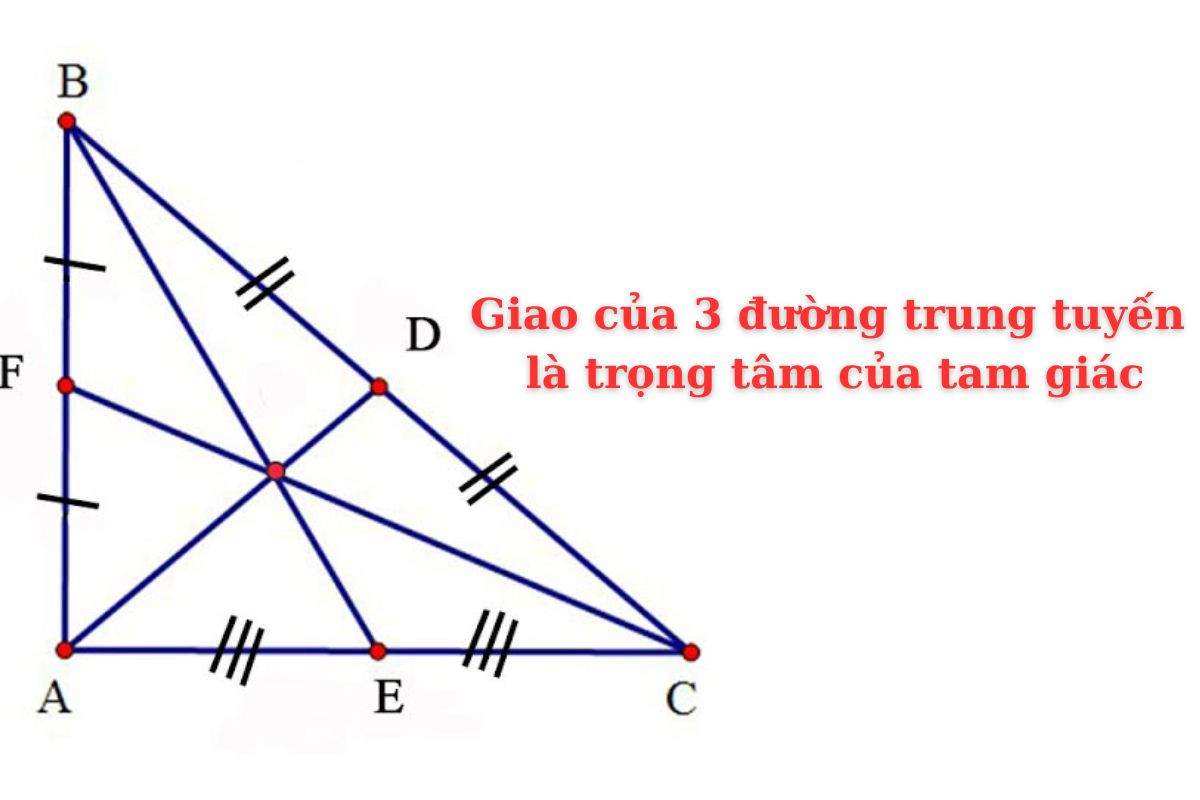
Theo quy ước trong toán học, khoảng cách từ trọng tâm của một tam giác đến đỉnh bất kỳ bằng ⅔ độ dài đường trung tuyến tương ứng với đỉnh đó. Nhờ tính chất này, bạn có thể xác định được khoảng cách từ trọng tâm đến đỉnh của tam giác dễ dàng. Do đó, hiểu đường trung tuyến là gì và nắm rõ các tính chất của đường trung tuyến là rất quan trọng.
Các định lý đường trung tuyến trong một tam giác
Sau khi đã hiểu rõ đường trung tuyến là gì, bạn cần nắm vững các định lý về đường trung tuyến trong tam giác để vận dụng giải các bài toán có liên quan. Dưới đây là các định lý quan trọng về đường trung tuyến trong tam giác:
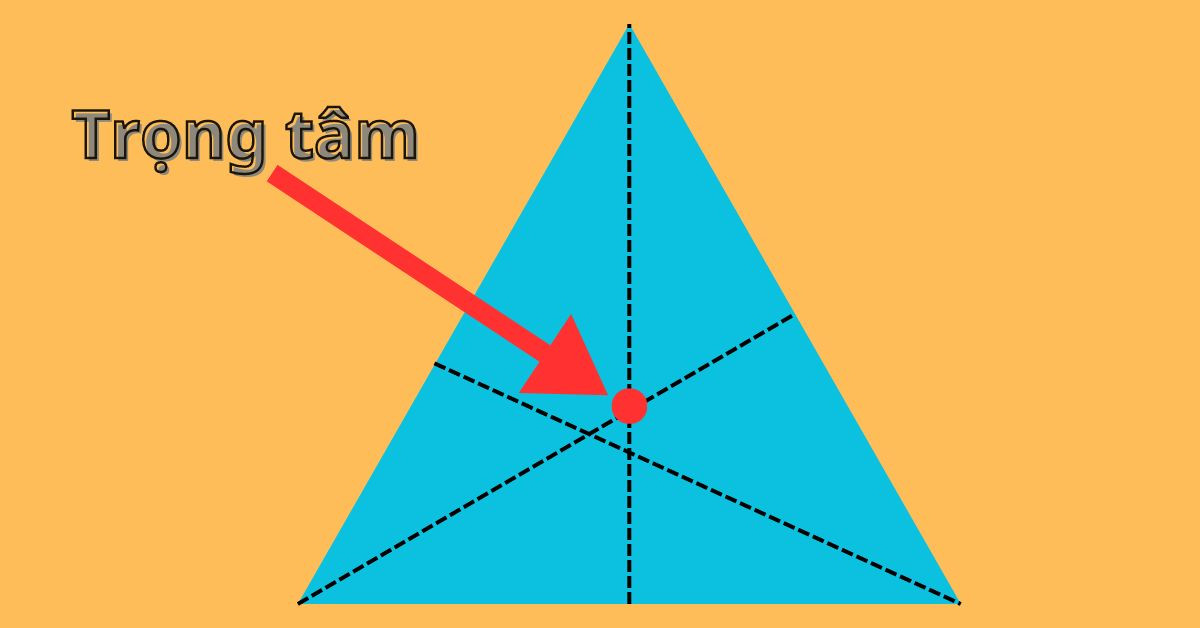
- Định lý 1 về đường trung tuyến: Ba đường trung tuyến của một tam giác cùng đi qua và giao nhau tại một điểm, điểm đó chính là trọng tâm của tam giác và cách đều 3 đỉnh của tam giác đó.
- Định lý 2 về đường trung tuyến: Đường trung tuyến đi qua đỉnh của tam giác và chia tam giác đó thành 2 tam giác nhỏ có diện tích như nhau. Ba đường trung tuyến đi qua 3 đỉnh của tam giác chia tam giác đó thành 6 tam giác nhỏ có diện tích bằng nhau.
- Định lý 3 về đường trung tuyến: Khoảng cách từ trọng tâm của tam giác đến các đỉnh bằng ⅔ độ dài của đường trung tuyến.
Nắm vững các định lý trên sẽ giúp bạn dễ dàng tính được độ dài của các đường trung tuyến trong một tam giác cũng như chứng minh được các tính chất của nó trong các dạng tam giác khác nhau. Hơn nữa, thông qua định lý về đường trung tuyến trong tam giác, bạn có thể xác định được dạng tam giác và vận dụng vào các bài toán liên quan.
Công thức tính độ dài của đường trung tuyến mới nhất
Tùy theo từng dạng tam giác mà công thức tính độ dài đường trung tuyến trong tam giác cũng khác nhau. Sau khi hiểu rõ đường trung tuyến là gì và nắm vững tính chất của nó, bạn sẽ dễ dàng tính được độ dài.
Công thức xác định độ dài đường trung tuyến trong tam giác thường
Trong tam giác bất kỳ, 3 đường trung tuyến có độ dài khác nhau và phụ thuộc vào độ dài 3 cạnh của tam giác đó. Dưới đây là công thức tính độ dài 3 đường trung tuyến trong tam giác theo định lý Apollonius mà bạn có thể tham khảo để vận dụng:
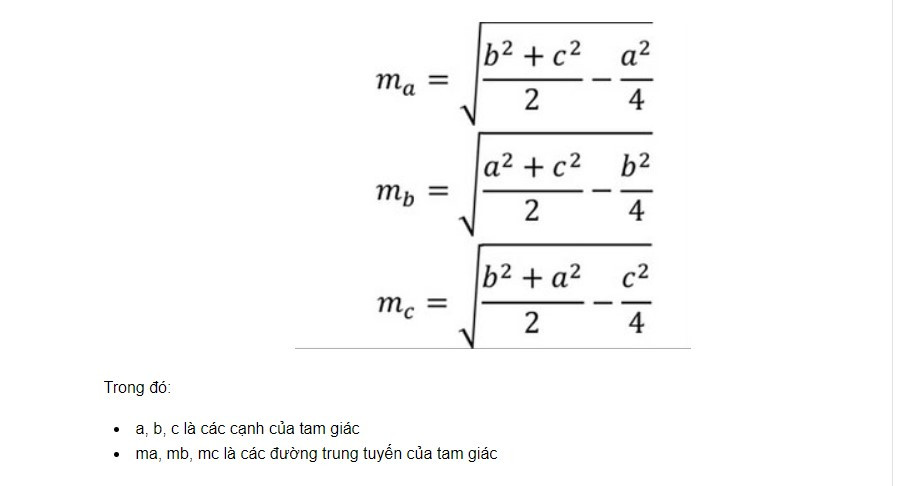
Công thức đường trung tuyến trong một tam giác vuông
Dựa vào đường trung tuyến là gì và tính chất đường trung tuyến trong tam giác vuông, bạn sẽ dễ dàng tính được độ dài của đường trung tuyến. Cụ thể, trong tam giác vuông, đường trung tuyến ứng với cạnh huyền thì bằng nửa cạnh huyền. Còn đường trung tuyến ứng với cạnh góc vuông thì công thức tính độ dài sẽ khác so với đường trung tuyến ứng với cạnh huyền.
Công thức tính độ dài đường trung tuyến trong một tam giác vuông:
- Đường trung tuyến ứng với cạnh huyền: m = c/2 (m là độ dài đường trung tuyến, c là độ dài cạnh huyền).
- Đường trung tuyến ứng với cạnh góc vuông:
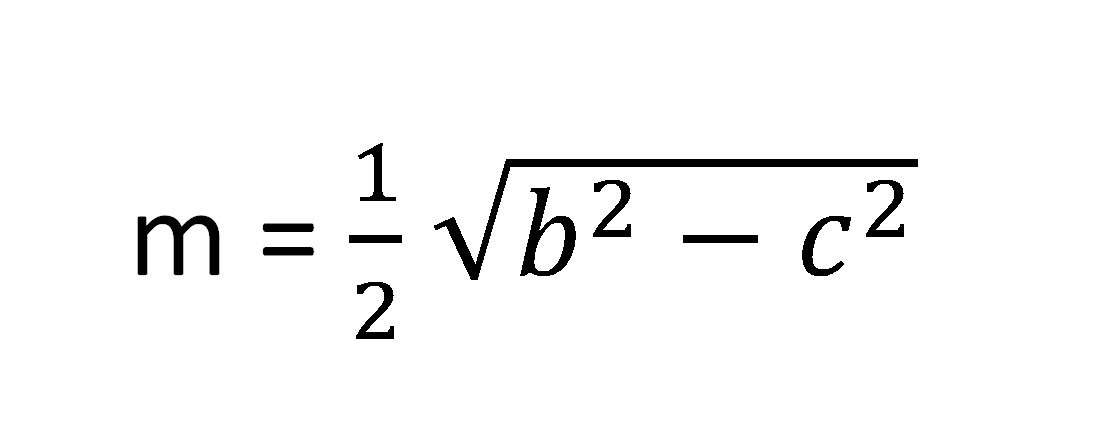
Các dạng toán về đường trung tuyến
Để hiểu rõ hơn đường trung tuyến là gì, bạn có thể tham khảo các dạng bài tập liên quan đến đường trung tuyến trong tam giác dưới đây:
Bài 1: Cho tam giác ABC cân tại A, biết AB = AC = 8 cm, BC = 10 cm. M là trung điểm BC. Độ dài đường trung tuyến AM là :
A. 20 cm
B. 2 cm
C. 5 cm
D. 8 cm
=> Đáp án đúng là C vì AM = ½ BC
Bài 2: Tam giác ABC có trung tuyến AM = 12 cm và trọng tâm G. Độ dài đoạn thẳng AG là:
A. 5,5 cm
B. 3 cm
C. 8 cm
D. 4 cm
=> Đáp án đúng là C vì AG = ⅔ AM = ⅔ * 12 = 8 cm.
Bài 3: Cho tam giác ABC bất kỳ có hai đường trung tuyến BM và CN. Nếu độ dài BM = CN thì tam giác ABC là tam giác gì?
A. Tam giác đều
B. Tam giác vuông
C. Tam giác cân
D. Tam giác vuông cân
=> Đáp án đúng là A vì tam giác đều có độ dài các đường trung tuyến bằng nhau.
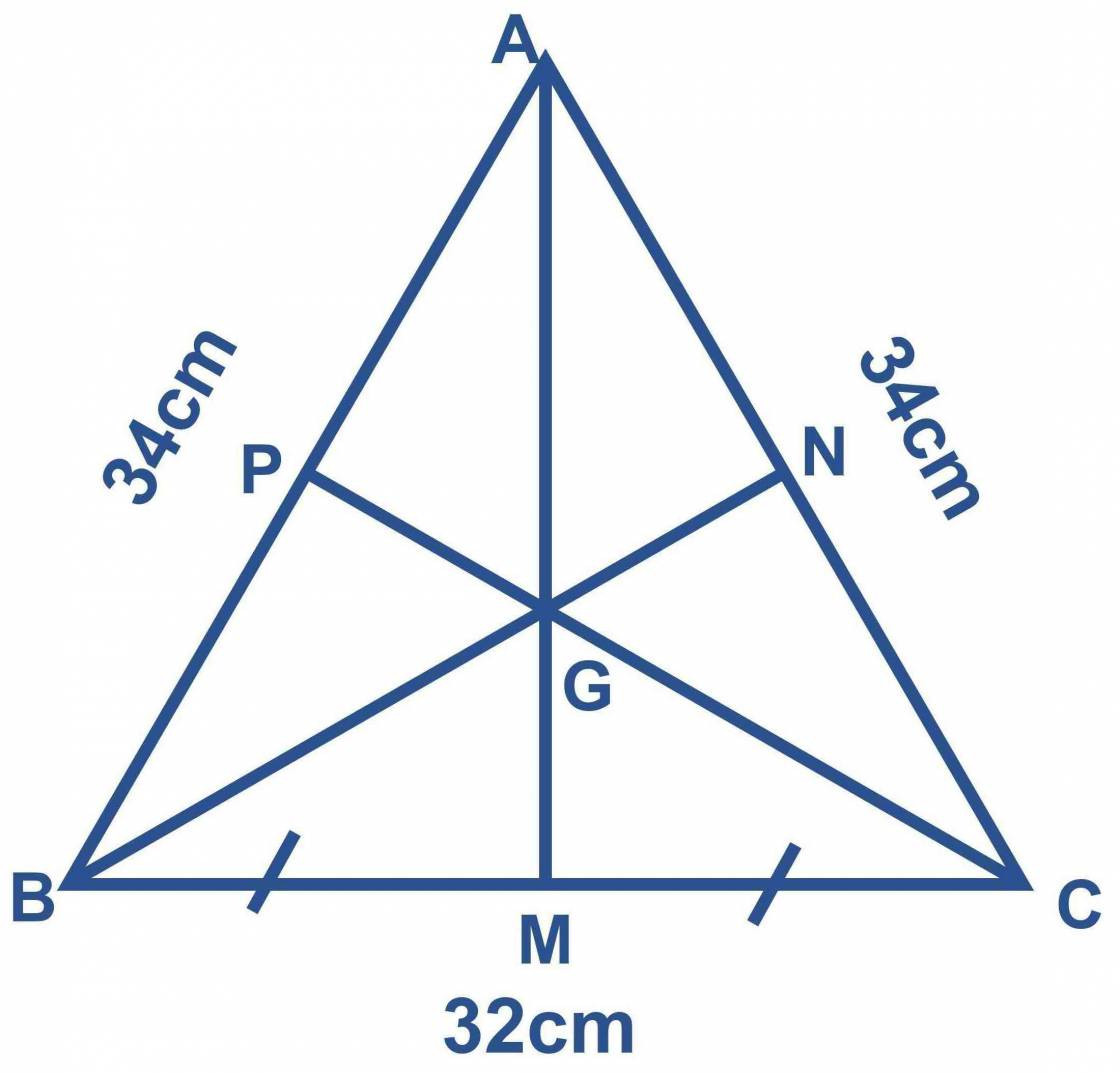
Mỗi tam giác có mấy đường trung tuyến?
Mỗi tam giác có ba đường trung tuyến. Đường trung tuyến của một tam giác chính là đoạn thẳng nối từ một đỉnh của tam giác với trung điểm của cạnh đối diện với đỉnh đó. Do đó, mỗi tam giác có ba đỉnh, và từ mỗi đỉnh đó, có thể vẽ ra một đường trung tuyến. Do đó, mỗi tam giác đều có ba đường trung tuyến và các đường trung tuyến cắt nhau tại một điểm gọi là trọng tâm của tam giác.
Việc tìm hiểu đường trung tuyến là gì và nắm vững tính chất đường trung tuyến trong tam giác sẽ giúp bạn dễ dàng xác định được độ dài của đường trung tuyến và các cạnh trong một tam giác. Mỗi kiểu tam giác sẽ có tính chất đường trung tuyến khác nhau nên trước khi tính toán độ dài đường trung tuyến, bạn cần biết chính xác đó là đường trung tuyến trong tam giác gì.
