Khái quát chung về hình lập phương
Hình lập phương là một đa diện đều trong không gian ba chiều, được định nghĩa bởi các đặc điểm sau:
- Mặt: Gồm 6 mặt đều là hình vuông.
- Cạnh: Gồm 12 cạnh bằng nhau.
- Đỉnh: Gồm 8 đỉnh, mỗi đỉnh là giao điểm của 3 cạnh.
- Đường chéo: Gồm 4 đường chéo, mỗi đường chéo cắt nhau tại một điểm và chia đôi các cạnh đối diện.
Ngoài ra, để tính diện tích xung quanh hình lập phương hay bất kỳ số đo nào khác, người ta quy ước các thông số sau:
- a: Độ dài cạnh hình lập phương
- P: Chu vi hình lập phương
- S(bm): Diện tích xung quanh hình lập phương
- S(xq): Diện tích xung quanh hình lập phương
- S(tp): Diện tích toàn phần hình lập phương
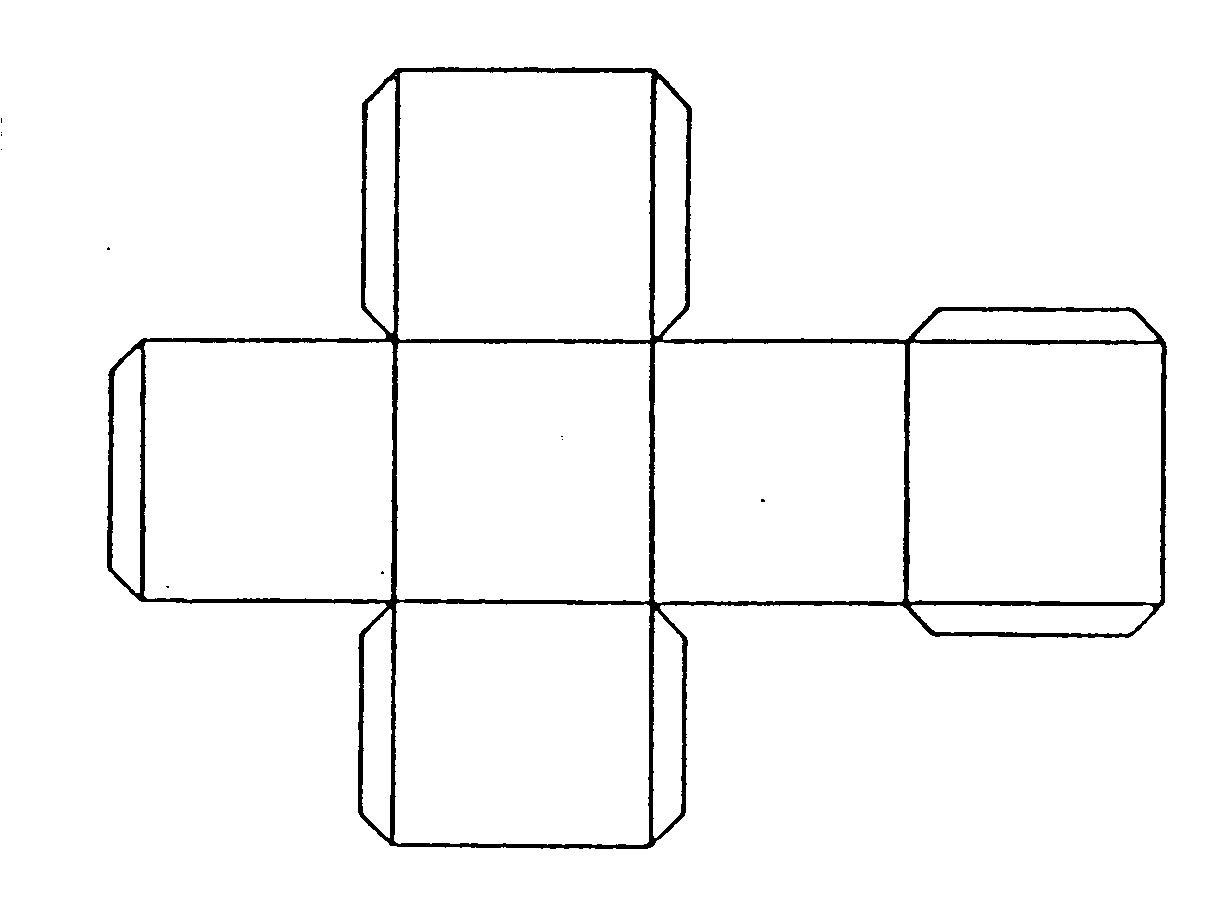
Diện tích xung quanh hình lập phương
Diện tích xung quanh hình lập phương là tổng diện tích của các mặt không bao gồm đáy của hình lập phương.
Công thức tính diện tích xung quanh hình lập phương
Công thức chuẩn nhất để tính diện tích xung quanh hình lập phương:
S(xq) =4a^2 (tương đương với a*a*4)
Trong đó:
- S(xq) là diện tích xung quanh hình lập phương.
- a là cạnh của hình lập phương.
Giải thích công thức: Hình lập phương có 6 mặt, trong đó 4 mặt là mặt xung quanh. Diện tích của mỗi mặt xung quanh là a^2 (tức là diện tích hình vuông). Do có 4 mặt xung quanh nên diện tích xung quanh của hình lập phương bằng tổng diện tích của 4 mặt xung quanh, được tính bằng: 4a^2.
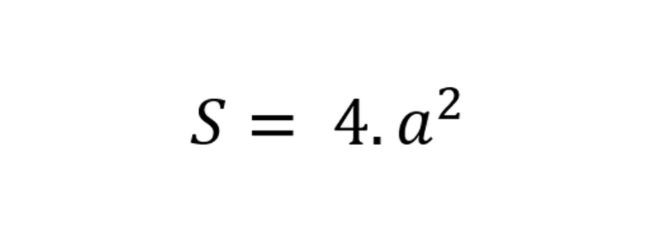
Ví dụ minh họa
Tính diện tích xung quanh một hình lập phương có độ dài cạnh là 2cm.
Trả lời:
Diện tích xung quanh của hình lập phương này là: 2 x 2 x 4 =16( Cm2)
Đáp số: 16cm2
Một số bài tập về hình lập phương
Dưới đây là một số ví dụ minh họa từ cơ bản đến nâng cao về nhóm bài tập thuộc diện tích xung quanh hình lập phương tính toán trên công cụ máy tính online.
Bài tập cơ bản
Câu 1: Tính diện tích xung quanh của hình lập phương có cạnh dài 10 cm
Công thức tính diện tích xung quanh của hình lập phương: S(xq) =a*a*4
Áp dụng công thức với cạnh dài a=10cm, ta có: S(xq) = 10*10*4=400cm2
Câu 2: Người ta làm một cái hộp carton dạng hình lập phương có cạnh dài 10cm. Tính diện tích bìa carton cần dùng để làm xung quanh hộp.
Đáp số: 400cm2
Câu 3: Người ta xếp một số viên gạch hình hộp chữ nhật tạo thành khối gạch hình lập phương cạnh 1m. Hãy tính diện tích xung quanh của khối gạch hình lập phương.
Đáp số: 4m2
Câu 4: Một bể kính nuôi cá dạng hình lập phương có cạnh 0,4m. Tính diện tích kính để làm bể cá đó (biết bể không có nắp và đáy của bể làm bằng kim loại).
Bể cá dạng hình lập phương có 6 mặt, trong đó không có nắp và đáy làm bằng kim loại. Do đó, để tính diện tích kính làm bể cá, ta chỉ cần tính diện tích của 4 mặt xung quanh.
Công thức tính diện tích xung quanh hình lập phương: S(xq) =a*a*4 = 0,4 * 0,4 * 4= 0,64m2.
Đáp số: 0,64m2

Câu 5: Hà dán giấy màu xung quanh một hộp quà hình lập phương cạnh dài 2dm. Hỏi diện tích giấy đã dán là bao nhiêu xen-ti-mét vuông?
Hà dán giấy màu xung quanh hộp quà hình lập phương, nghĩa là chỉ dán lên các mặt xung quanh mà không dán đáy. Do đề bài cho đơn vị dm nhưng lại đặt câu hỏi với đơn vị cm nên ta cần tính diện tích giấy màu đã dán rồi đổi sang đơn vị xen-ti-mét vuông (cm²).
Lời giải:
Công thức tính diện tích xung quanh của chiếc hộp: S(xq) =a*a*4 = 2 * 2 * 4= 16 dm2.
Đổi 16dm2 = 1600cm2
Do đó, diện tích giấy đã dán là 1600cm2.
Bài tập nâng cao
Bài 1: Hai hình lập phương có độ dài cạnh lần lượt là 3 cm và 4 cm. Diện tích xung quanh của hình lập phương nào lớn hơn hình lập phương kia bao nhiêu?
Gợi ý: Tính diện tích xung quanh của từng hình lập phương, sau đó lấy diện tích xung quanh của hình lập phương lớn trừ đi diện tích xung quanh của hình lập phương nhỏ.
Bài 2: Một khối rubik có dạng hình lập phương với cạnh dài 3 cm. Nếu mỗi mặt của khối rubik được tô màu khác nhau thì tổng diện tích các mặt được tô màu là bao nhiêu?
Gợi ý: Tính diện tích một mặt của khối rubik, sau đó nhân với 6 (số mặt của khối rubik).
Bài 3: Một căn phòng dạng lập phương có chiều dài 6m. Người ta muốn sơn toàn bộ các bức tường (không bao gồm cả cửa ra vào và cửa sổ) của căn phòng. Biết diện tích cửa ra vào và cửa sổ là 12 m². Tính diện tích tường cần sơn.
Gợi ý: Tính diện tích xung quanh của căn phòng, sau đó trừ đi diện tích cửa ra vào và cửa sổ.
Bài 4: Một ngôi nhà hình lập phương có cạnh dài 10 m. Để sơn toàn bộ mặt ngoài của ngôi nhà (không bao gồm mái nhà), cần bao nhiêu kg sơn? (Biết 1 kg sơn phủ được 5 m² và giá 1 kg sơn là 50.000 đồng). Tính tổng chi phí sơn nhà.
Gợi ý: Tính diện tích xung quanh của ngôi nhà, sau đó nhân với giá 1 kg sơn và số kg sơn cần thiết.
Bài 5: Thiết kế một hộp quà hình lập phương có kích thước phù hợp để đựng một món quà có dạng hình cầu có đường kính 8 cm. Tính diện tích tối thiểu của giấy màu cần dùng để bọc hộp quà (không bao gồm đáy hộp).
Gợi ý: Tính bán kính của hình cầu, sau đó tính diện tích xung quanh hình lập phương có cùng chiều cao và bán kính với hình cầu. Diện tích xung quanh này chính là diện tích tối thiểu của giấy màu cần dùng để bọc hộp quà.
Bài 6: Một công ty sản xuất hộp đựng quà dạng hình lập phương. Kích thước của hộp quà cần đảm bảo thể tích chứa được tối thiểu 27 cm³. Biết giá thành để sản xuất một chiếc hộp tỉ lệ thuận với diện tích xung quanh của hộp. Tìm kích thước cạnh của hộp quà tối thiểu để công ty sản xuất có thể thu được lợi nhuận cao nhất.
Gợi ý: Tính thể tích hình lập phương cần thiết, sau đó tìm ra cạnh của hình lập phương đó. Tính diện tích xung quanh của hình lập phương này.
Bài tập tự luyện
Bài 1: Một hình lập phương có cạnh dài 5 cm. Tính diện tích xung quanh hình lập phương đó.
Bài 2: Một bể cá hình lập phương có cạnh dài 6 dm. Tính diện tích kính cần dùng để làm bể cá đó (không tính nắp và đáy bể).
Bài 3: Một hộp quà hình lập phương có cạnh dài 30 cm. Bạn An muốn dán giấy màu xung quanh hộp quà đó. Hỏi bạn An cần bao nhiêu diện tích giấy màu?
Bài 4: Hai hình lập phương có cạnh dài lần lượt là 3 cm và 4 cm. Tỉ số diện tích xung quanh của hai hình lập phương đó là bao nhiêu?
Bài 5: Một khối gỗ hình lập phương có cạnh dài 8 cm. Người ta sơn tất cả các mặt của khối gỗ đó. Tính diện tích cần sơn.
Bài 6: Một căn phòng hình lập phương có chiều dài mỗi cạnh 6 m. Người ta muốn sơn tất cả các bức tường (bao gồm cả cửa sổ và cửa ra vào) của căn phòng đó. Biết diện tích mỗi ô cửa sổ là 2 m² và diện tích mỗi cánh cửa là 1,5 m². Tính diện tích cần sơn. (Giả sử các bức tường tiếp xúc nhau mà không có khe hở).
Bài 7: Một cửa hàng bán đồ chơi trẻ em có các khối lập phương nhựa với nhiều kích cỡ khác nhau. Khối lập phương nhỏ nhất có cạnh dài 2 cm, giá bán 5000 đồng. Để làm một mô hình trang trí, bạn Nam cần mua 12 khối lập phương nhỏ nhất này. Hỏi bạn Nam cần trả bao nhiêu tiền, tổng diện tích xung quanh của chúng là bao nhiêu?
Bài 8: Một công ty sản xuất hộp quà tặng hình lập phương từ bìa cứng. Để tiết kiệm chi phí, công ty quyết định không dán giấy màu lên đáy hộp. Hộp quà có kích thước theo yêu cầu của khách hàng là: cạnh dài 15 cm. Tính diện tích bìa cứng cần dùng để sản xuất một hộp quà theo kích thước trên.
Bài 9: Một bể bơi hình lập phương có thể tích là 125 m³. Tính diện tích xung quanh của bể bơi đó.
Cách vẽ hình lập phương nhanh nhất
Các bài tập tính diện tích xung quanh hình lập phương thường yêu cầu vẽ hình minh họa, để có thể nhanh chóng giải quyết bài toán, hãy thử vận dụng cách vẽ hình nhanh như sau:
Bước 1: Vẽ mặt đáy hình bình hành
- Vẽ tứ giác ABCD theo hình dạng hình bình hành.
- Đánh dấu các điểm A, B, C, D là các đỉnh của tứ giác.
Bước 2: Dựng các đường cao
- Từ mỗi đỉnh A, B, C, D, kẻ đường cao vuông góc với mặt phẳng ABCD.
- Gọi các chân đường cao lần lượt là A', B', C', D'.
- Đảm bảo độ dài của mỗi đường cao bằng cạnh a của hình lập phương cần vẽ.
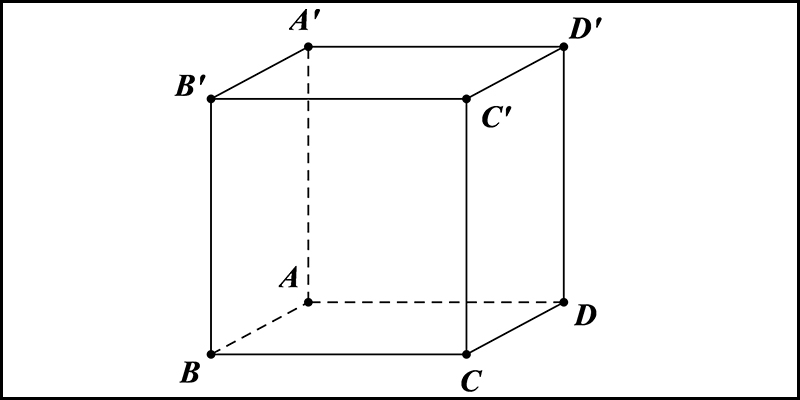
Bước 3: Hoàn thiện hình lập phương
- Nối các điểm A', B', C', D' bằng các đường thẳng.
- Ta thu được hình lập phương ABCDA'B'C'D'.
Những ứng dụng của hình lập phương trong cuộc sống
Hình lập phương là một hình khối cơ bản trong toán học và có nhiều ứng dụng trong nhiều lĩnh vực khác nhau của đời sống. Bạn có thể bắt gặp các khối hình này ở một số nơi, chẳng hạn:
- Trong xây dựng và kiến trúc: Cấu trúc hình lập phương mang lại sự ổn định, vững chắc và khả năng chịu lực cao cho các công trình. Ví dụ: Khối Rubik khổng lồ tại Thành phố New York (Mỹ).
- Trong đóng gói và vận chuyển: Do khả năng tận dụng tối đa không gian và dễ dàng xếp chồng lên nhau nên dạng lập phương được ứng dụng nhiều trong đóng gói. Ví dụ: Hộp carton, thùng container, pallet.
- Trong khoa học và kỹ thuật: Hình lập phương được sử dụng để mô phỏng cấu trúc của các chất rắn ở cấp độ nguyên tử, giúp nghiên cứu và phát triển vật liệu mới. Ví dụ: Mạng tinh thể kim cương.
- Trong toán học và giáo dục: Hình lập phương là một đơn vị đo lường thể tích trong không gian ba chiều, được sử dụng để giải các bài toán về hình học, vật lý và kỹ thuật. Hình lập phương cũng được sử dụng để dạy học sinh về các khái niệm toán học cơ bản như diện tích, thể tích, góc, cạnh,...
Luyện tập là chìa khóa giúp học sinh thành thạo việc tính diện tích xung quanh hình lập phương. Thông qua các bài tập đa dạng, học sinh sẽ rèn luyện được khả năng tư duy logic, vận dụng công thức chính xác và giải quyết vấn đề một cách hiệu quả.
