Định nghĩa tam giác vuông
Để hiểu bản chất công thức diện tích tam giác vuông, bạn cần nắm rõ định nghĩa và tính chất của hình này.
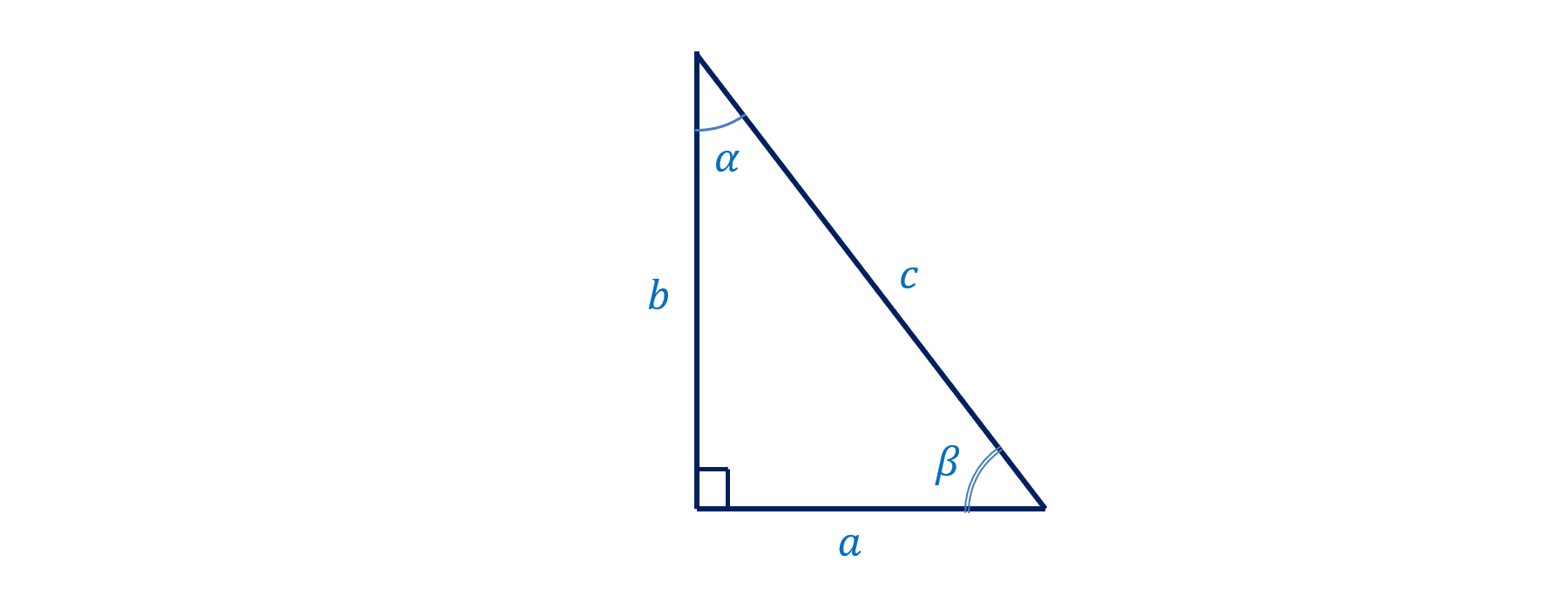
Tam giác vuông là tam giác có một góc vuông, tức là có số đo bằng 90 độ, ký hiệu là ∠B. Hai cạnh kề với góc vuông được gọi là cạnh góc vuông (hay cạnh bên), thường được ký hiệu là a và b. Cạnh đối diện với góc vuông ∠B được gọi là cạnh huyền, được ký hiệu là c và là cạnh dài nhất trong tam giác vuông. Hai góc nhọn còn lại (góc A và C) được gọi là góc nhọn và phụ nhau, nghĩa là ∠A+∠C=90.
Trong tam giác vuông, nếu một cạnh góc vuông được chọn làm cạnh đáy, thì cạnh góc vuông còn lại sẽ là đường cao tương ứng với cạnh đáy đó. Còn nếu đường cao của tam giác vuông hạ từ một đỉnh vuông góc xuống cạnh đối diện được gọi là đường cao tương ứng với cạnh huyền.
Định lý Pythagoras khẳng định rằng trong một tam giác vuông, bình phương độ dài cạnh huyền bằng tổng bình phương độ dài hai cạnh góc vuông. Công thức: c^2 =a^2 +b^2
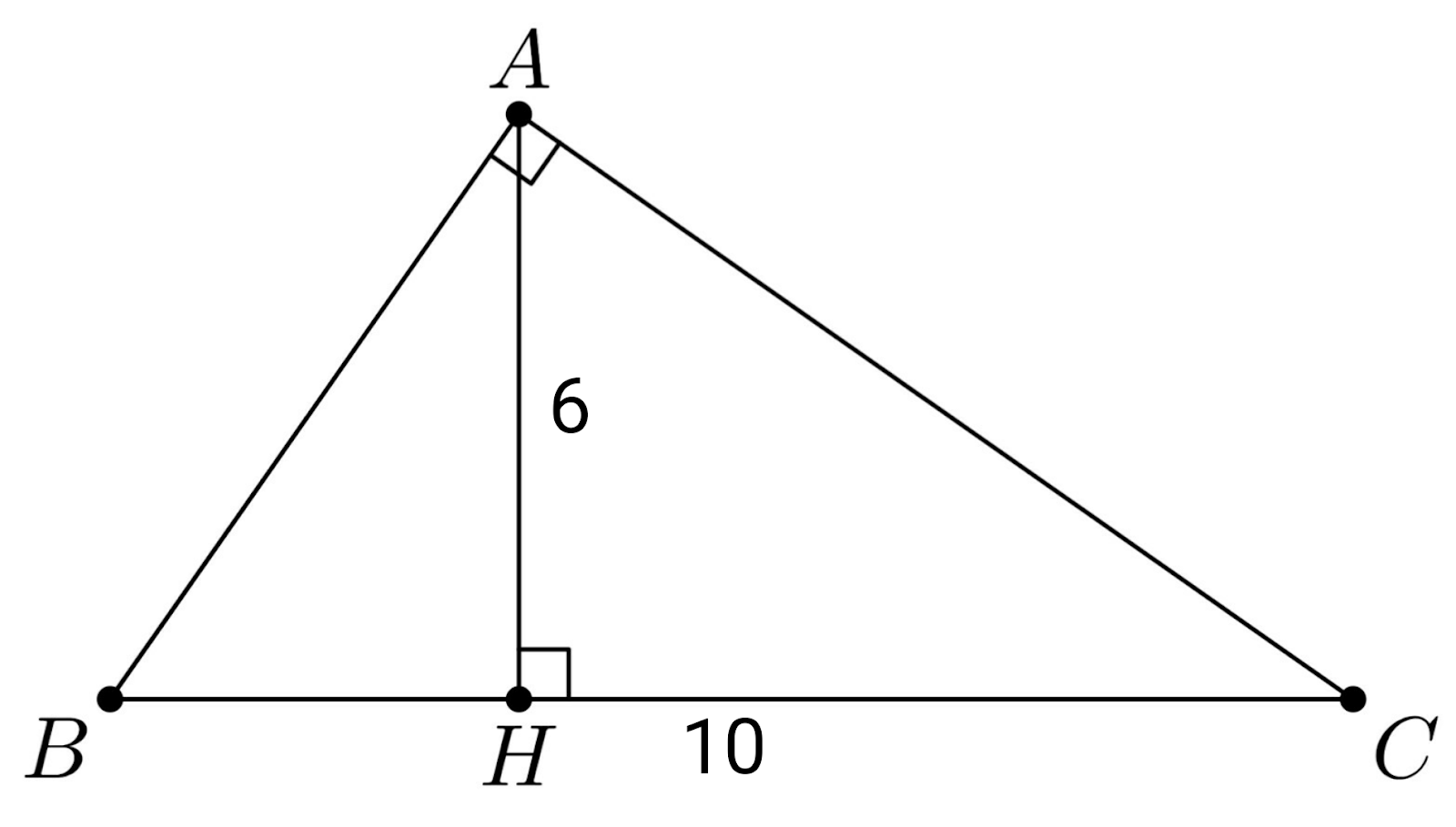
Các công thức để tính diện tích tam giác vuông
Thực tế, có rất nhiều công thức để tính diện tích của một hình tam giác vuông, bạn có thể tham khảo.
Công thức cơ bản
Diện tích tam giác vuông S bằng một nửa tích cạnh huyền c và chiều cao h hạ từ đỉnh vuông góc xuống cạnh huyền, được biểu thị bằng công thức: S= ½*c*h
Giải thích: Công thức tính diện tích tam giác vuông dựa trên mối liên hệ giữa tam giác vuông và hình bình hành. Khi ta sao chép một tam giác vuông bất kỳ, xoay hình sao chép đó 180 độ rồi ghép hai hình tam giác lại với nhau, ta sẽ có một hình bình hành. Diện tích Sb của hình bình hành bằng tích của độ dài cạnh đáy b và chiều cao h tương ứng: Sb =b * h mà diện tích tam giác ban đầu bằng 1 nửa diện tích hình bình hành. Do đó là có công thức như trên.
Ví dụ: Cho tam giác vuông có cạnh huyền c=11,7 cm và chiều cao h=5,1 cm. Diện tích tam giác S được tính như sau:
S= 1/2 *11,7 * 5,1≈30(cm 2 )

Công thức Pythagoras
Tương truyền, nhà toán học Pythagoras đã phát hiện ra công thức này trong khi chờ đợi để giao gạch lót vuông cho Bạo chúa Polycrates tại đảo Samos, Hy Lạp cổ đại. Tuy nhiên, các bằng chứng lịch sử cho thấy Pythagoras không phải là người đầu tiên tìm ra công thức này. Trên thực tế, công thức diện tích tam giác vuông bằng một nửa tích hai cạnh góc vuông đã được biết đến từ các nền văn minh cổ đại như Lưỡng Hà, Trung Quốc hay ở Ai Cập.
Khi ta ghép hai tam giác vuông giống nhau theo cạnh huyền, ta sẽ tạo thành một hình chữ nhật với chiều dài bằng độ dài cạnh góc vuông a và chiều rộng bằng độ dài cạnh góc vuông b.
Diện tích của hình chữ nhật bằng tích của chiều dài a và chiều rộng b = a * b
Diện tích của tam giác vuông bằng một nửa diện tích của hình chữ nhật và tương ứng:
S = ½ *a * b
Ví dụ: Cho tam giác vuông có hai cạnh góc vuông a=6 cm và b=10 cm. Diện tích S của tam giác vuông này được tính bằng máy tính online casio fx-580vn:
S= ½ * a * b= ½ * 5 * 10 =30(cm2)
Công thức Heron
Công thức Heron được đặt theo tên của nhà toán học, kỹ sư Hy Lạp cổ đại Hero xứ Alexandria, sống vào thế kỷ 1 sau Công nguyên. Tuy nhiên, có ý kiến cho rằng Archimedes, nhà toán học vĩ đại nhất lịch sử, đã biết đến công thức này trước đó tận hai thế kỷ.
Công thức diện tích tam giác vuông này thường được sử dụng khi ta biết độ dài ba cạnh của tam giác nhưng không biết chiều cao.
S= √p(p−a)(p−b)(p−c)
Trong đó:
- p là chu vi tam giác, s= (a+b+c)
- a, b, c là độ dài ba cạnh của tam giác

Công thức lượng giác
Sử dụng định nghĩa sin trong tam giác thu được công thức: sin(C) = h / b
=> h = b * sin(C).
Thay thế phép tính chiều cao trên vào công thức diện tích tam giác dạng cơ bản, ta có:
S = ( a * b * sin (C) ) / 2.
Hay đơn giản hóa, ta có diện tích S của tam giác có thể được tính bằng công thức lượng giác:
S= ½ * ab * sin(C)
Trong đó:
- a, b là độ dài hai cạnh kề với góc C
- C là góc nhọn nằm giữa hai cạnh a và b
Ví dụ: Cho tam giác vuông có hai cạnh kề góc C là a=6 cm và b=11.7 cm, góc C=59 ∘. Diện tích S của tam giác vuông này được tính bằng:
S= 1/2 * 6* 11.7 *sin(59∘)≈30(cm2)
Tan góc giữa cạnh góc vuông và cạnh huyền
Công thức tính diện tích tam giác vuông bằng tan góc được suy ra từ định lý Pythagoras, một định lý toán học quan trọng được phát triển bởi nhà toán học Hy Lạp Pythagoras (570 – 495 TCN).
Diện tích S của tam giác vuông có thể được tính bằng công thức tan góc:
S= ½ * ab * tan(A)
Trong đó:
- a, b là độ dài hai cạnh góc vuông
- A là góc nhọn kề với cạnh a
Cho tam giác vuông có hai cạnh góc vuông là a=6 cm và b=11.7 cm, góc A=59∘. Diện tích S của tam giác vuông này được tính bằng:
S= ½ * 6 * 11.7 * tan(59∘) ≈ 30(cm2)
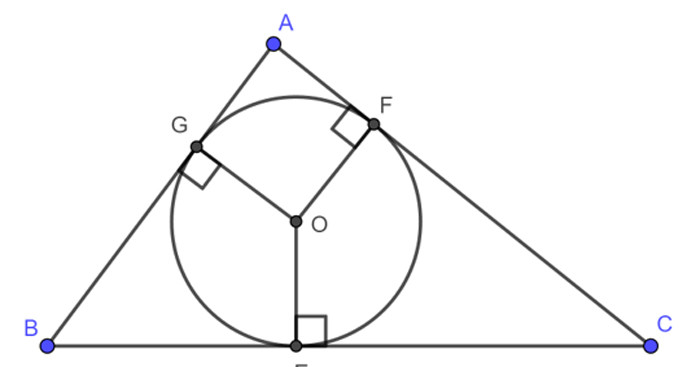
Đường tròn nội tiếp tam giác vuông
Công thức tính bán kính đường tròn nội tiếp tam giác vuông được phát hiện bởi nhà toán học Ấn Độ Brahmagupta (598–668 sau Công nguyên) và được ghi chép trong tác phẩm "Brahmasphutasiddhanta" của ông. Do đó, công thức này còn được gọi là "công thức Brahmagupta".
S = Pr/ 2
Suuy ra:
r= 2S/P
Trong đó:
- r:bán kính đường tròn nội tiếp
- p: chu vi của hình tam giác
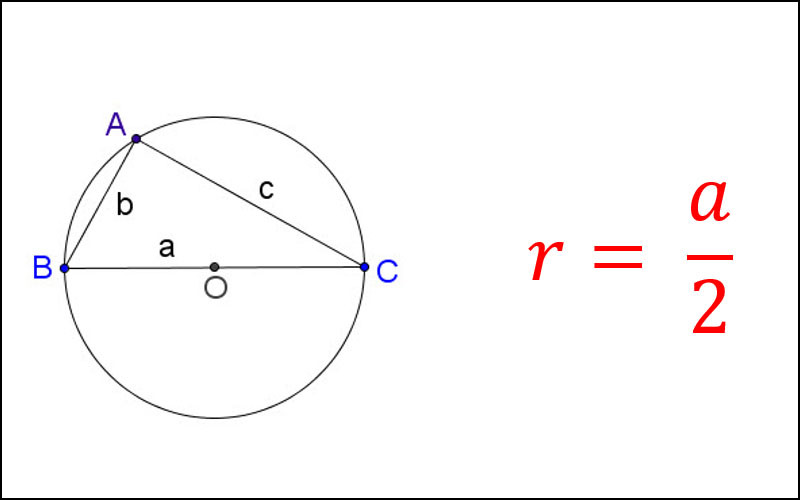
Đường tròn ngoại tiếp tam giác vuông
Bán kính R của đường tròn ngoại tiếp tam giác vuông có thể được tính bằng công thức: R= abc/ 4S
Trong đó:
- S là diện tích tam giác vuông
- a, b, c là độ dài ba cạnh của tam giác vuông (c là cạnh huyền)
Công thức cho tam giác vuông cân
Diện tích S của tam giác vuông cân có thể được tính bằng nhiều công thức khác nhau, bao gồm:
Công thức cơ bản: S= 1/2 * a^2
Trong đó: a là độ dài cạnh góc vuông của tam giác vuông cân
Ví dụ: Cho tam giác vuông cân có độ dài cạnh góc vuông là a=6 cm. Diện tích S của tam giác vuông cân này được tính bằng: S= ½ * 6^2 =18(cm2)
Các dạng bài tập từ cơ bản đến nâng cao
Bài 1: Cho tam giác vuông ABC có hai cạnh góc vuông AC = 3 cm, BC = 4 cm. Tính diện tích tam giác ABC.
Lời giải:
Áp dụng công thức diện tích tam giác vuông cơ bản:
S= 1/2 ⋅AC⋅BC= 1/2 ⋅3⋅4=6(cm2)
Bài 2: Cho tam giác vuông MNP có hai cạnh góc vuông MN = 5 cm, NP = 12 cm. Tính diện tích tam giác MNP.
Lời giải:
Áp dụng công thức diện tích tam giác vuông cơ bản:
S= ½ MN⋅NP= 1/2 ⋅5⋅12=30(cm2)
Bài 3: Cho tam giác vuông DEF có hai cạnh góc vuông DE = 7 cm, EF = 24 cm. Tính diện tích tam giác DEF.
Lời giải:
Áp dụng công thức diện tích tam giác vuông cơ bản:
S= ½ DE⋅EF= 1/2 ⋅7⋅24=84(cm2)
Bài 4: Cho tam giác vuông GHI có cạnh góc vuông GH = 15 cm và góc kề cạnh GH là 45 độ. Tính diện tích tam giác GHI.
Lời giải:
Xác định cạnh góc vuông còn lại:
Do góc kề cạnh GH là 45 độ, nên tam giác GHI là tam giác vuông cân.
Do đó, cạnh góc vuông còn lại HI = GH = 15 cm.
Tính diện tích tam giác vuông:
S= ½ ⋅GH⋅HI= ½ ⋅15⋅15=112.5(cm2)
Bài 5: Cho tam giác vuông DEF có cạnh góc vuông DE = 8 cm và góc kề cạnh DE là 30 độ. Tính diện tích tam giác DEF.
Lời giải:
Xác định cạnh góc vuông còn lại:
DF=DE⋅tan(30∘)=8⋅tan(30∘)=43(cm)
Tính diện tích tam giác vuông:
S= 1/2 ⋅DE⋅DF= 1/2 ⋅8⋅43 =163 (cm2)
Bài 6: Cho tam giác vuông GHI có cạnh góc vuông GH = 10 cm và góc kề cạnh GH là 60 độ. Tính diện tích tam giác GHI.
Lời giải:
Xác định cạnh góc vuông còn lại:
GI=GH⋅tan(60∘)=10⋅tan(60∘)=103 (cm)
Tính diện tích tam giác vuông:
S= ½ ⋅GH⋅GI= ½ ⋅10⋅103 =503 (cm2)

Một số bài tự luyện:
Bài 1: Cho tam giác vuông ABC có hai cạnh góc vuông AC = 4 cm, BC = 6 cm và đường cao AH chia cạnh huyền BC thành hai đoạn BH = 2 cm và HC = 4 cm. Tính diện tích tam giác ABC và diện tích tam giác AHC.
Bài 2: Cho tam giác vuông MNP có hai cạnh góc vuông MN = 5 cm, NP = 12 cm và đường trung tuyến MI. Biết đường trung tuyến MI chia tam giác vuông MNP thành hai tam giác vuông cân IMP và INP. Tính diện tích tam giác MNP và diện tích tam giác IMP.
Bài 3: Cho tam giác vuông DEF có cạnh huyền EF = 13 cm và góc nhọn D = 45 độ. Kẻ đường cao DH vuông góc với cạnh huyền EF. Tính diện tích tam giác vuông DEF, diện tích tam giác DEH và diện tích tam giác DFH.
Bài tập vận dụng:
Bài 1: Một mảnh đất hình tam giác vuông có hai cạnh góc vuông dài 8 m và 12 m. Tính diện tích mảnh đất đó và đề xuất một số phương án sử dụng diện tích mảnh đất đó cho mục đích sinh hoạt và sản xuất.
Bài 2: Một hình hộp chữ nhật có chiều dài 6 dm, chiều rộng 4 dm và chiều cao 5 dm. Tính diện tích toàn phần của hình hộp chữ nhật đó và giải thích ý nghĩa của việc tính diện tích toàn phần trong thực tế.
Bài 3: Một bể bơi hình thang có đáy lớn 10 m, đáy nhỏ 8 m và chiều cao 4 m. Tính diện tích đáy và diện tích xung quanh của bể bơi đó. Biết rằng bể bơi được lát gạch có diện tích 120 m2, hãy tính chi phí lát gạch cho bể bơi (giả sử giá mỗi viên gạch là 20.000 đồng).
Bài 4: Một khu đất hình tam giác vuông có hai cạnh góc vuông dài 200 m và 300 m. Người ta xây dựng một nhà máy hình chữ nhật có diện tích 1500 m2 trên khu đất đó. Biết rằng một cạnh của nhà máy nằm dọc theo một cạnh góc vuông của khu đất và chiều dài nhà máy bằng 1/2 cạnh góc vuông còn lại. Tính chiều rộng nhà máy và vẽ sơ đồ khu đất và nhà máy trên đó.
Bài 5: Một mảnh vườn hình chữ nhật có chiều dài 25 m và chiều rộng 15 m. Người ta muốn chia mảnh vườn thành hai phần bằng một đường thẳng vuông góc với một cạnh của mảnh vườn để trồng rau và hoa. Biết rằng diện tích phần đất trồng rau bằng 2/3 diện tích phần đất trồng hoa. Tính diện tích mảnh đất trồng rau và vẽ sơ đồ mảnh vườn sau khi chia.
Tam giác vuông có mấy đường cao?
Một tam giác vuông có 3 đường cao. Trong tam giác vuông, hai cạnh góc vuông là hai đường cao tương ứng với hai cạnh kề. Đường cao thứ ba được kẻ từ đỉnh góc vuông xuống cạnh huyền. Vì vậy, tổng cộng có 3 đường cao trong một tam giác vuông. Vận dụng điều này sẽ giúp bạn dễ dàng tính diện tích tam giác vuông.
Nắm vững công thức và luyện tập thường xuyên là chìa khóa giúp học sinh chinh phục các bài toán diện tích tam giác vuông. Việc ghi nhớ chính xác các công thức và phân chia bài tập hợp lý sẽ giúp học sinh giải quyết vấn đề nhanh chóng và hiệu quả.
