Tìm hiểu lý thuyết về hình chữ nhật
Trước khi đi sâu vào cách tính diện tích hình chữ nhật, hãy cùng tìm hiểu về hình dạng này một cách khái quát.
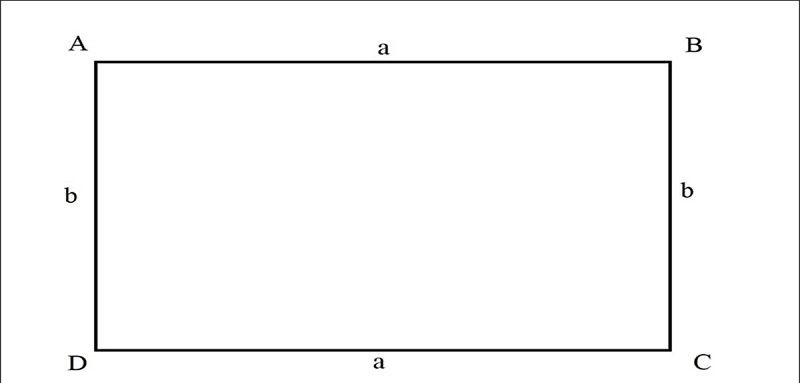
Hình chữ nhật là một hình học phổ biến, thường xuất hiện trong cuộc sống và học tập. Nó được định nghĩa là một hình có bốn cạnh, trong đó hai cạnh đối diện song song và có độ dài bằng nhau. Đặc điểm này tạo nên một hình dạng đặc trưng, dễ nhận biết và ứng dụng.
Một đặc điểm nổi bật của hình chữ nhật là các góc của nó, mỗi góc đều là góc vuông, tức 90 độ. Điều này không chỉ làm cho hình chữ nhật trở nên đặc biệt trong hình học mà còn giúp chúng ta dễ dàng hình dung và tính toán các thuộc tính khác của nó. Ngoài ra, hình chữ nhật có hai đường chéo có độ dài bằng nhau và chia hình chữ nhật thành hai tam giác bằng nhau.
Công thức tính diện tích hình chữ nhật
Trong hình học, việc tính diện tích của hình chữ nhật là một kỹ năng cơ bản nhưng vô cùng quan trọng. Dưới đây là các công thức liên quan đến diện tích hình chữ nhật.
Diện tích hình chữ nhật
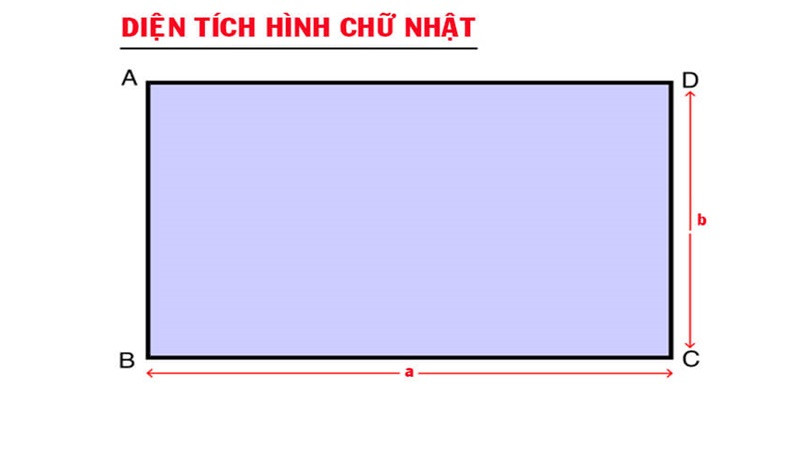
Diện tích của hình chữ nhật được tính bằng cách nhân hai kích thước của nó với nhau. Trong đó, kích thước dài nhất được gọi là chiều dài, còn kích thước ngắn hơn, vuông góc với chiều dài, được gọi là chiều rộng.
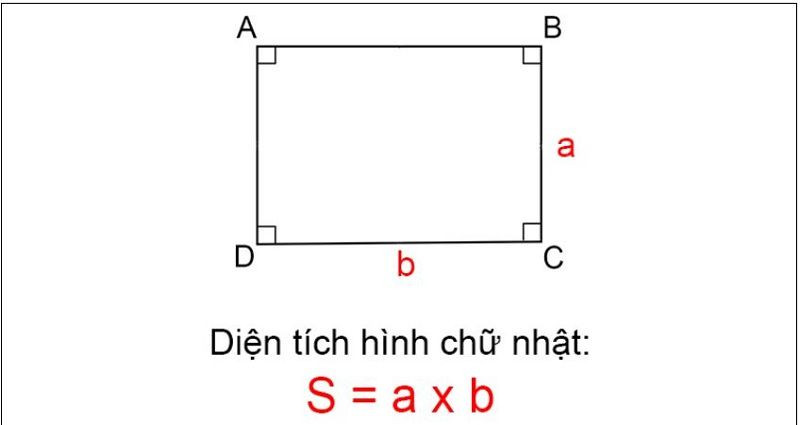
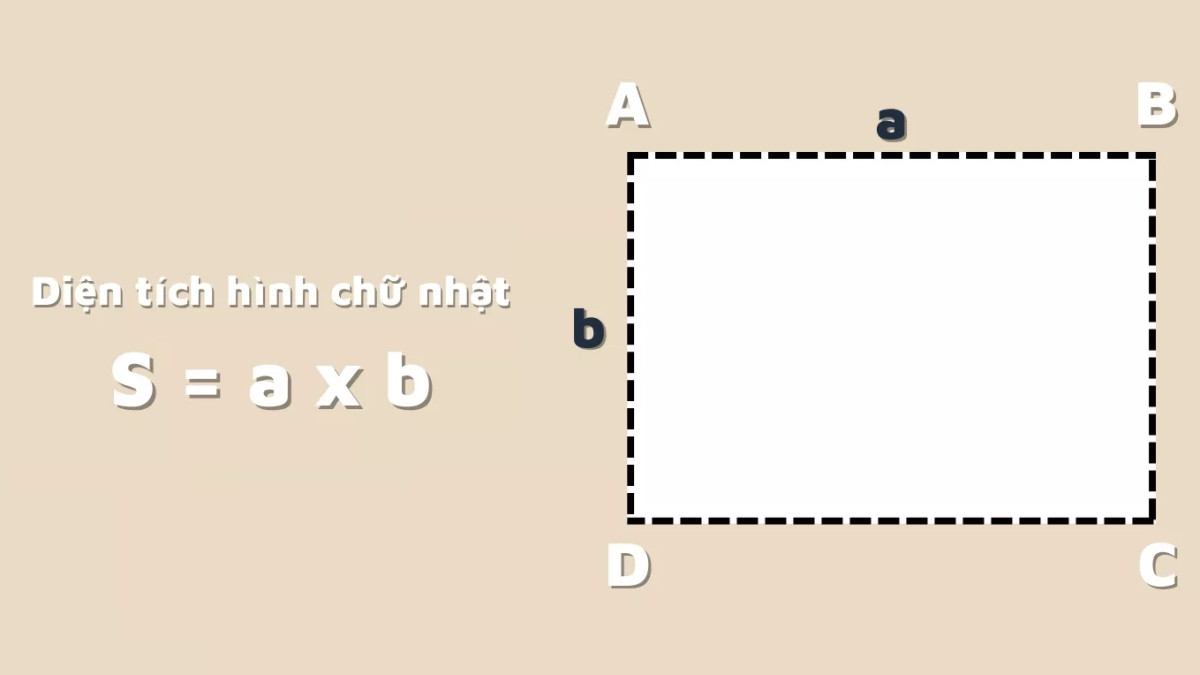
Công thức tính diện tích của hình chữ nhật như sau: S = a x b
Trong đó: a là chiều dài, b là chiều rộng của hình chữ nhật.
Diện tích hình hộp chữ nhật
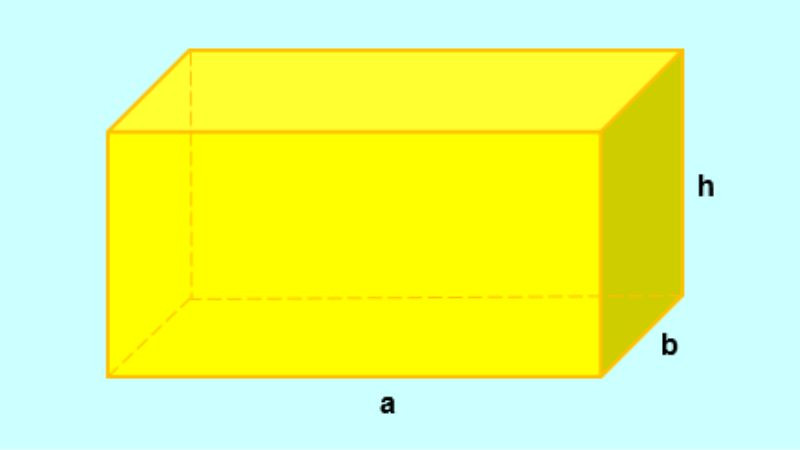
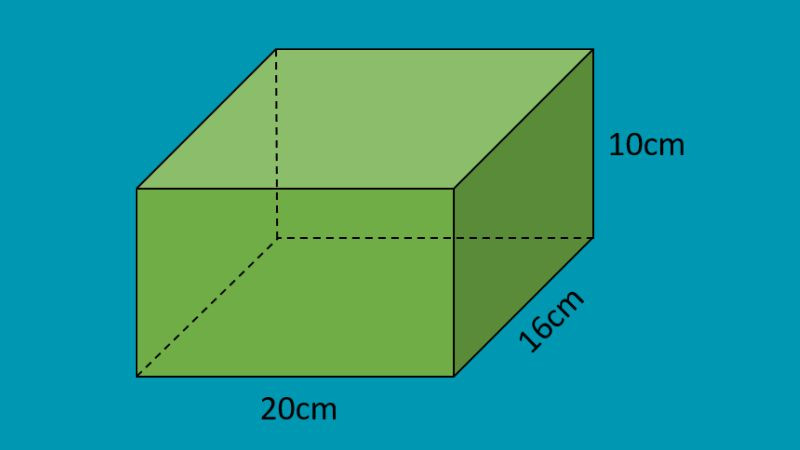
Hình hộp chữ nhật là một hình khối ba chiều, được tạo thành từ sáu mặt hình chữ nhật. Để tính diện tích của hình hộp chữ nhật, ta cần tính tổng diện tích của sáu mặt chữ nhật này.
Giả sử hình hộp chữ nhật có chiều dài là a, chiều rộng là b và chiều cao là c. Theo công thức tính diện tích hình chữ nhật, ta có, tổng diện tích của hình hộp chữ nhật là:
Diện tích toàn phần = 2ab + 2ac + 2bc = 2(ab + ac + bc)
Công thức tổng quát: Diện tích hình hộp chữ nhật = 2(ab + ac + bc)
Trong đó: a, b, c lần lượt là chiều dài, chiều rộng và chiều cao của hình hộp chữ nhật.
Diện tích xung quanh hình hộp chữ nhật
Khi nói đến hình hộp chữ nhật, ta có thể phân biệt ba khái niệm: diện tích mặt đáy, diện tích xung quanh và diện tích toàn phần.
Diện tích mặt đáy của hình chữ nhật là diện tích được tính trên một bề mặt đáy của hình hộp chữ nhật, bằng cách nhân chiều dài với chiều rộng, như công thức quen thuộc: S = a × b.
Còn diện tích xung quanh hình hộp chữ nhật là tổng diện tích của các mặt bao quanh hình khối này. Công thức tính diện tích xung quanh như sau:
Diện tích xung quanh = 2ac + 2bc = 2(a + b)c
Trong đó: a là chiều dài, b là chiều rộng và c là chiều cao của hình chữ nhật.
Diện tích xung quanh phản ánh tổng diện tích của các mặt bao quanh hình khối, trong khi diện tích mặt phẳng chỉ tính trên một mặt phẳng duy nhất.
Diện tích toàn phần hình hộp chữ nhật
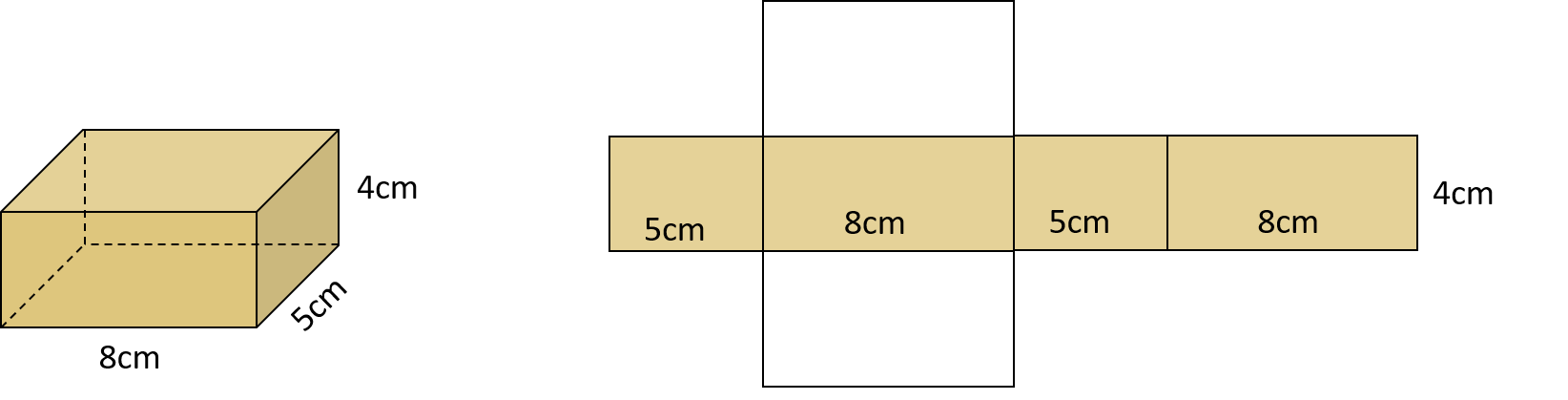
Diện tích toàn phần hình hộp chữ nhật bằng tổng diện tích xung quanh của hình hộp chữ nhật và 2 mặt còn lại.
Công thức:
Stp = Sxq + 2 x a x b = 2h x (a + b) + 2 x a x b
Trong đó:
Stp là kí hiệu diện tích toàn phần hình hộp chữ nhật
Sxq là kí hiệu diện tích xung quanh hình hộp chữ nhật
a là kí hiệu chiều dài hình hộp chữ nhật
b là kí hiệu chiều rộng hình hộp chữ nhật
h là kí hiệu chiều cao hình hộp chữ nhật
Những dạng toán thường gặp về diện tích hình chữ nhật
Hình chữ nhật là một trong những hình học cơ bản và phổ biến nhất, thường xuất hiện trong các bài toán liên quan đến diện tích và thể tích. Khi làm các bài toán liên quan đến diện tích hình chữ nhật, học sinh thường gặp phải một số dạng toán điển hình. Cùng tham khảo các dạng bài tập thường gặp dưới đây:
Tính diện tích hình chữ nhật khi cho trước độ dài hai cạnh
Muốn tính diện tích hình chữ nhật, công thức cơ bản là S = a × b, trong đó a là chiều dài và b là chiều rộng của hình chữ nhật. Vì vậy, nếu chúng ta biết chiều dài của hai cạnh, việc tính diện tích trở nên rất đơn giản.
Giả sử chúng ta biết chiều dài của hai cạnh là a và b, thì công thức tính diện tích sẽ là: S = a × b
Ví dụ, nếu một hình chữ nhật có chiều dài là 6 cm và chiều rộng là 3 cm, thì diện tích của hình chữ nhật này sẽ là:
S = 6 cm × 3 cm = 18 cm²
Diện tích của hình chữ nhật này là 15 cm².
Tính diện tích hình chữ nhật khi biết độ dài một cạnh và độ dài đường chéo
Trong một số trường hợp, thay vì biết chiều dài của cả hai cạnh, chúng ta chỉ biết chiều dài của một cạnh và đường chéo của hình chữ nhật. Tuy nhiên, việc tính diện tích vẫn có thể thực hiện được.
Giả sử chúng ta biết chiều dài của một cạnh là a và đường chéo là d. Từ đây, chúng ta có thể tính được chiều dài của cạnh còn lại b bằng công thức:
b = √(d^2 - a^2)
Sau khi đã tìm được chiều dài của hai cạnh, việc tính diện tích trở nên rất đơn giản: S = a × b
Ví dụ, nếu một hình chữ nhật có chiều dài một cạnh là 3 cm và đường chéo là 5 cm, thì: b = √(5^2 - 3^2) = √(25 - 9) = √16 = 4 cm
Diện tích của hình chữ nhật này sẽ là:
S = 3cm × 4cm = 12cm²
Tính diện tích của hình chữ nhật lớn khi biết diện tích của các hình chữ nhật nhỏ
Trong một số trường hợp, chúng ta không trực tiếp biết chiều dài của các cạnh của hình chữ nhật lớn. Thay vào đó, chúng ta chỉ biết diện tích của các hình chữ nhật nhỏ hơn được tạo thành từ hình chữ nhật lớn đó.
Ví dụ, hãy giả sử chúng ta có một hình chữ nhật lớn được chia thành 4 hình chữ nhật nhỏ, mỗi hình có diện tích là 9 cm². Để tính diện tích của hình chữ nhật lớn, chúng ta chỉ cần cộng diện tích của 4 hình chữ nhật nhỏ:
Diện tích hình chữ nhật lớn = 9 cm² + 9 cm² + 9 cm² + 9 cm² = 36 cm²
Phương pháp này được tính toán bằng công cụ máy tính casio online rất hữu ích khi chúng ta cần tính diện tích của các hình dạng phức tạp được cấu thành từ nhiều hình chữ nhật nhỏ hơn. Bằng cách tính diện tích của từng hình chữ nhật nhỏ, chúng ta có thể tính được diện tích của toàn bộ hình dạng lớn hơn.
Tính độ dài 1 cạnh khi biết diện tích và độ dài cạnh còn lại
Đặc biệt, khi chúng ta biết diện tích hình chữ nhật cho trước và chiều dài của một cạnh, chúng ta có thể tính được chiều dài của cạnh còn lại. Đây là một bài toán khá phổ biến trong toán học.
Giả sử chúng ta có một hình chữ nhật với chiều dài một cạnh là a và diện tích là S. Từ đây, chúng ta có thể tính được chiều dài của cạnh còn lại b bằng công thức: b = S / a
Ví dụ, nếu một hình chữ nhật có chiều dài một cạnh là 4 cm và diện tích là 24 cm², thì:
b = 24 cm² / 4 cm = 6 cm
Như vậy, chiều dài của cạnh còn lại là 6 cm.
Mẹo để tính diện tích hình chữ nhật nhanh và chính xác
Để tính diện tích hình chữ nhật một cách nhanh chóng và chính xác, bạn có thể áp dụng một số phương pháp hiệu quả sau:
Trước tiên, hãy luôn ghi nhớ công thức cơ bản: Diện tích = Chiều dài x Chiều rộng. Đây là nền tảng quan trọng nhất.
Khi làm việc với các số liệu, hãy chắc chắn rằng tất cả đều cùng một đơn vị đo. Nếu không, hãy chuyển đổi chúng về cùng một đơn vị để tránh sai sót. Ví dụ, nếu chiều dài được đo bằng mét và chiều rộng bằng centimet, hãy chuyển đổi tất cả sang mét hoặc centimet trước khi tính toán.
Sử dụng máy tính là một cách tuyệt vời để đảm bảo độ chính xác của phép nhân, đặc biệt khi bạn xử lý các con số lớn hoặc muốn kiểm tra lại kết quả của mình.
Một mẹo hữu ích khác là vẽ một hình chữ nhật với các kích thước đã cho. Điều này không chỉ giúp bạn hình dung rõ ràng vấn đề mà còn đảm bảo bạn sử dụng đúng các giá trị cho chiều dài và chiều rộng.
Cuối cùng, việc thực hành thường xuyên sẽ giúp bạn trở nên nhanh nhẹn và chính xác hơn trong khi tính toán diện tích hình chữ nhật. Càng làm nhiều bài tập, bạn sẽ càng dễ dàng ghi nhớ công thức và áp dụng một cách tự nhiên.
Ứng dụng tính diện tích hình chữ nhật vào thực tế
Việc tính toán diện tích hình chữ nhật không chỉ là một bài toán thuần túy trong toán học, mà còn có rất nhiều ứng dụng thực tế trong cuộc sống hàng ngày. Dưới đây là một số ví dụ về cách chúng ta có thể sử dụng kiến thức về tính diện tích hình chữ nhật:
- Thiết kế và tính toán diện tích các không gian sống: Khi thiết kế nhà ở, văn phòng, cửa hàng,.. việc tính toán diện tích các phòng, khu vực là rất quan trọng để đảm bảo không gian sử dụng hiệu quả và phù hợp với nhu cầu.
- Tính toán diện tích sàn nhà, diện tích mặt bằng: Trong xây dựng, việc tính toán chính xác diện tích sàn nhà, diện tích mặt bằng là cần thiết để lên kế hoạch, dự trù vật liệu và chi phí.
- Tính toán diện tích mặt bằng cửa hàng, siêu thị: Các cửa hàng, siêu thị cần tính toán diện tích sàn để bố trí các khu vực hợp lý, tối ưu hóa không gian kinh doanh.
- Tính toán diện tích các tấm vật liệu xây dựng: Khi mua các tấm vật liệu như gạch, gỗ, kính,... để xây dựng, chúng ta cần tính toán diện tích chính xác để dự trù đủ vật liệu.
- Tính toán diện tích các bản in, kích thước hình ảnh: Trong lĩnh vực in ấn, quảng cáo, thiết kế đồ họa, việc tính toán diện tích các bản in, kích thước hình ảnh là rất quan trọng.

Như vậy, khả năng tính toán diện tích hình chữ nhật là một kỹ năng vô cùng cần thiết và được ứng dụng rộng rãi trong nhiều lĩnh vực thực tế của cuộc sống. Nắm vững các kiến thức và phương pháp tính toán này sẽ giúp chúng ta giải quyết nhiều vấn đề một cách hiệu quả.
